![]()
Statystyka wykład z dnia 13 maja 2000 r.
Gdy mamy:
t1 y1
t2 y2
t3 y3
.. ..
.. ..
tn yn
1. przyrosty absolutne
jednopodstawowe
jeżeli za podstawę przyjmiemy y1
y2-y1 , y3-y1 , y4-y1 ,........... yn-y1
jeżeli y5
y2-y5, y2-y5 , y3-y5 , ……… yn-y5
łańcuchowe
y2-y1 , y3-y2 , y4-y3 , ............... yn-yn-1
2. przyrosty względne
jednopodstawowe
![]()
łańcuchowe
![]()
3. indeks
Indeksem (wskaźnikiem dynamiki) nazywamy każdą liczbę względną powstałą przez podzielenie wielkości danego zjawiska w okresie badanym przez wielkość tego zjawiska w okresie podstawowym
![]()
i>1 - wzrost danego zjawiska
i=1 - nie zmienia się
i<1 - spadek poziomu danego zjawiska
jednopodstawowe
![]()
łańcuchowe
![]()
Rozpatrzymy ilość rozwodów w okresie 1970 -1977 r.
za bazę przyjmujemy rok 1970 - y1
lata |
rozwody w tys. |
Przyrost absolutny |
Przyrost względny |
Indeks |
|||
|
|
jednopods. |
łańcuch. |
jednopodst. w % |
łańcuch. w % |
jednopodst. w % |
łańcuch. W % |
1970 1971 1972 1973 1974 1975 1976 1977 |
34,6 36,3 37,4 39,7 39,7 41,3 38,0 43,2 |
0 1,7 2,8 5,1 5,1 6,7 3,4 8,6 |
-- 1,7 1,1 2,3 0 1,6 -3,3 5,2 |
0,0 4,9 8,1 14,7 14,7 19,4 9,8 24,9 |
-- 4,9 3,0 6,1 0 4,0 -8.0 13,7 |
100 104,9 108,1 114,7 114,7 119,4 109,8 124,9 |
-- 104,9 103,0 106,1 100 104,0 -92 113,7 |
Indeksy
P - cena
P0 - cena w okresie podstawowym
P1 - cena w okresie badanym
Q - ilość
Q0 - ilość w okresie podstawowym
Q1 - ilość w okresie badanym
W - wartość
W0 - wartość w okresie podstawowym
W1 - wartość w okresie badanym
indeksy indywidualne
ip - indeks cen ![]()
- wyraża relację poziomu cen określonego dobra w okresie badanym i podstawowym
iq - indeks ilości ![]()
- wyraża relację produkcji
iw - indeks wartości ![]()
, ![]()
indeksy zespolone
Iw - indeks zespolony wartości
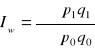
Indeks Laspegresa - ustala się to do czego się odnosi w okresie podstawowym
Indeks Peaschyego - ustala się w okresie badanym |teraźniejszym|
indeks ceny
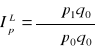
indeks Laspegresa
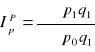
indeks Peaschyego
indeks ilości
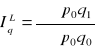
indeks Laspegresa
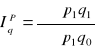
indeks Peaschego
![]()
- indeks Fishera
![]()
indeks ceny
![]()
indeks ilości