PYTANIA NA EGZAMIN LICENCJACKI

Zestaw 1.

1. Zbieżność ciągu liczbowego.

2. Definicja całki Riemanna.

3. Definicja i przykłady grup.

Zestaw 2.

1. Kres górny i dolny zbioru
   

2. Podstawowe twierdzenie rachunku całkowego.

3. Dzielnik normalny grupy i grupa ilorazowa.

Zestaw 3.

1. Pochodna funkcji jednej zmiennej i jej interpretacja.

2. Twierdzenie o całkowaniu przez części.

3. Odwzorowanie liniowe - definicja i przykłady.

Zestaw 4.

1. Ciągłość funkcji - warunki równoważne ciągłości.

2. Twierdzenie o całkowaniu przez podstawienie.

3. Opis macierzowy odwzorowania liniowego.

Zestaw 5.

1. Ciągłość, jednostajna ciągłość, warunek Lipschitza.

2. Ważne klasy funkcji całkowalnych.

3. Baza i wymiar przestrzeni liniowej.

Zestaw 6.

1. Zbieżność szeregów liczbowych - kryteria zbieżności.

2. Własności całki Riemanna.

3. Rząd macierzy.

Zestaw 7.

1. Zbieżność punktowa i jednostajna ciągu funkcyjnego.

2. Całka niewłaściwa z funkcji nieograniczonej. Przykład.

3. Wyznacznik macierzy.

Zestaw 8.

1. Wzór Taylora.

2. Całka niewłaściwa po przedziale nieograniczonym. Przykład.

3. Rozwiązalność układu m równań liniowych z n niewiadomymi.

Zestaw 9.

1. Twierdzenie o trzech ciągach.

2. Jak się bada zbieżność całki niewłaściwej?

3. Rozwiązalność układu n równań liniowych z n niewiadomymi.

Zestaw 10.

1. Zbieżność ciągu monotonicznego. Określenie liczby e.

2. Obliczanie długości krzywej.

3. Mnożenie macierzy, a złożenie odwzorowań liniowych.

Zestaw 11.

1. Własność Darboux.

2. Obliczanie pól obszarów płaskich.

3. Macierz odwrotna.

Zestaw 12.

1. Własności funkcji ciągłej na przedziale domkniętym i ograniczonym.

2. Kiedy funkcja f(x)=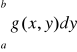
   jest ciągła?

3. Jądro i obraz odwzorowania liniowego.

Zestaw 13.

1. Pochodna sumy, iloczynu i ilorazu funkcji jednej zmiennej.

2. Kiedy funkcja f(x)=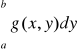
   jest różniczkowalna?

3. Wartości i wektory własne.

Zestaw 14.

1. Pochodna funkcji złożonej.

2. Całka krzywoliniowa niezorientowana. Określenie i interpretacja.

3. Schemat Bernoulliego.

Zestaw 15.

1. Twierdzenie de l'Hospitala.

2. Całka krzywoliniowa zorientowana. Określenie i interpretacja.

3. Zmienna losowa - jej wartość oczekiwana i wariancja.

Zestaw 16.

1. Ekstrema lokalne funkcji jednej zmiennej. Określenie i metody znajdowania.

2. Wzór Greena (dla płaskiej krzywej zamkniętej).

3. Niezależność zdarzeń i zmiennych losowych.

Zestaw 17.

1. Własności sumy szeregu potęgowego.

2. Różniczkowalność funkcji wielu zmiennych.

3. Prawo wielkich liczb.

Zestaw 18.

1. Kryterium Weierstrassa zbieżności jednostajnej szeregu.

2. Poszukiwanie ekstremów lokalnych funkcji dwóch zmiennych.

3. Prawdopodobieństwo warunkowe. Przykład zastosowania.

Zestaw 19.

1. Warunek Cauchy'ego a zbieżność ciągu.

2. Całka podwójna i całki iterowane.

3. Dystrybuanta zmiennej losowej i jej własności.

Zestaw 20.

1. Ciągłość granicy ciągu funkcji ciągłych.

2. Zamiana zmiennych w całce podwójnej.

3. Zmienna losowa dyskretna i ciągła.

Zestaw 21.

1. Definicja przestrzeni metrycznej. Przykład przestrzeni metrycznej.

2. Definicja i podstawowe własności przekształcenia liniowego.

3. Definicja zmiennej losowej. Charakterystyki liczbowe zmiennej losowej.

Zestaw 22.

1. Zbieżność ciągów w przestrzeni metrycznej. Definicja i przykład przestrzeni zwartej.

2. Wartości własne macierzy i przekształceń liniowych.

3. Przestrzeń probabilistyczna. Prawdopodobieństwo warunkowe, prawdopodobieństwo całkowite.

Zestaw 23.

1. Granica ciągu liczbowego. Zbieżność ciągów monotonicznych, liczba e.

2. Układy równań liniowych i ich rozwiązywanie.

3. Prawa wielkich liczb i ich interpretacja.

Zestaw 24.

1. Granica funkcji w punkcie. Ciągłość funkcji, przykłady.

2. Funkcja pierwotna, całka nieoznaczona, całkowanie przez części.

4. Centralne twierdzenie graniczne Lindberga- Levy'ego.

Zestaw 25.

1. Kryteria zbieżności szeregów liczbowych.

2. Ekstrema lokalne, warunek konieczny i warunki wystarczające istnienia ekstremum funkcji jednej zmiennej.

3. Definicja grupy i podgrupy. Przykłady.

Zestaw 26.

1. Ciągi funkcyjne, zbieżność punktowa i jednostajna.

2. Własności funkcji ciągłych na zbiorach zwartych.

3. Twierdzenie o przechodzeniu do granicy pod znakiem całki.

Zestaw 27.

1. Granica ciągu liczbowego, własności ciągów zbieżnych.

2. Definicja grupy i podgrupy, przykłady, Grupa ilorazowa.

3. Zmienna losowa, wartość oczekiwana, wariancja.

Zestaw 28.

1. Definicja granicy funkcji rzeczywistej zmiennej rzeczywistej w punkcie. Ciągłość funkcji w punkcie i na zbiorze.

2. Przestrzenie liniowe. Baza i wymiar przestrzeni liniowej.

3. Prawdopodobieństwo warunkowe. Twierdzenie o prawdopodobieństwie całkowitym.

Zestaw 29.

1. Własności funkcji ciągłych na przedziale domkniętym ograniczonym.

2. Zbieżność punktowa i jednostajna ciągów funkcyjnych. Kryterium Weierstrassa zbieżności jednostajnej szeregów funkcyjnych.

3. Rozkład prawdopodobieństwa. Przykłady rozkładów dyskretnych i ciągłych.

Zestaw 30.

1. Definicja pochodnej funkcji jednej zmiennej w punkcie. Warunek konieczny różniczkowalności funkcji.

2. Wyznacznik macierzy i jego wyznaczanie. Twierdzenie Cramera.

3. Zbiory przeliczalne i ich własności, przykłady.

---