Lista 2. Wybrane metody doboru zmiennych objaśniających do budowy modelu ekonometrycznego.

Zad.1. Dla poniższych zmiennych objaśniających obliczyć ich współczynniki zmienności

X₁: 10, 11, 15, 15, 12, 14, 20, 20, 22, 22

X₂: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

X₃: 12, 12, 12, 14, 12, 10, 12, 14, 12, 10.

Zad.2. Obliczyć współczynnik korelacji z próby statystycznej dla n = 12. Próba statystyczna dała wyniki:

xi	1	2	3	4	5	6	7	8	9	10	11	12
yi	2	3	4	5	6	7	8	9	10	11	12	13

Zad.3. Dla n = 18 otrzymano wartość współczynnika korelacji r = 0,35. Dla α = 0,05 odpowiednim testem statystycznym przetestować właściwą hipotezę H₀ względem alternatywnej H₁. Czy można uznać, że na podstawie powyższych wartości współczynnika korelacji z próby, między badanym wektorem losowym zachodzi statystycznie istotna zależność (liniowa)?

Zad.4. Mamy dane macierze współczynników korelacji dla zmiennych Y, X₁, X₂, X₃, X₄:

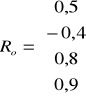
R =

R₀ - zawiera współczynniki korelacji Y z X_i (i = 1, 2, 3, 4);

R - zawiera współczynniki korelacji między X_i i X_j dla i, j = 1, 2, 3, 4

Wybrać optymalną kombinację zmiennych ze względu na:

a). poziom wskaźnika integralnej pojemności informacyjnej spośród kombinacji zawierających zmienną X₃;

b). metodą analizy macierzy współczynników korelacji R₀ i R(uwzględniając wartość krytyczną r* współczynnika korelacji, przyjmując α = 0,1 i n = 18)

c). współczynnik korelacji wielorakiej (spośród dwuelementowych kombinacji zmiennych objaśniających).

Zad.5. Na podstawie dwudziestu dwóch obserwacji (n = 22) dokonanych na zmiennych objaśniających i zmiennej objaśnianej (endogenicznej) obliczono współczynniki korelacji, które zestawiono w symetrycznej macierzy W:

Stosując metodę grafową wybrać optymalną kombinację zmiennych objaśniających do budowy modelu ekonometrycznego. Weryfikację istotności współczynników korelacji przeprowadzić na poziomie a=0,10.

Uwaga. Pierwszy wiersz macierzy W zawiera współczynniki korelacji zmiennych objaśniających ze zmienną objaśnianą.

---