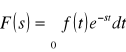
Przekształcenie Laplace'a i jego własności
by Dres (literą oznaczyłem znak transformaty, bo pierdolony MS Equator nie ma takiego znaczka :/)
Def.: Transformatą Laplace'a fukcji zmiennej rzeczywistej f(t) nazywamy funkcję F(s) zmiennej zespolonej niezależnej s = c + j, określoną wzorem:
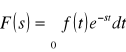
![]()
Funkcja f(t) jest oryginałem, a F(s) - transformatą (obrazem funkcji f(t) przez transformację Laplace'a).
Transformatą odwrotną nazywamy wyrażenie:
![]()
Własności transformaty Laplace'a:
liniowość
![]()
transformata sumy funkcji
![]()
transformata pochodnych funkcji
![]()
,
gdzie ![]()
jest wartością początkową funkcji f(t) w punkcie t = 0 z prawej strony (granica)
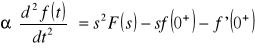
,
gdzie ![]()
jest pochodną ![]()
w praktyce ogólny wzór jest następujący:
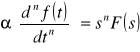
transformata całek funkcji
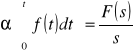
transformata funkcji okresowej
Tw. Jeżeli dana jest funkcja okresowa ![]()
, gdzie k = 1,2,3...
oraz 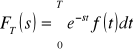
jest transformatą funkcji f(t) za jeden okres, to
![]()
twierdzenie o przesunięciu rzeczywistym
![]()
twierdzenie o przesunięciu zespolonym
![]()
gdzie jest dowolną liczbą zespoloną
twierdzenie o wartości końcowej
![]()
twierdzenie o wartości początkowej
![]()
Transformaty wybranych funkcji: