Miary zagrożenia (downside risk measures) - Miary zagrożenia opierają się na definicji ryzyka traktującej ryzyko jedynie jako możliwość zaistnienia sytuacji niekorzystnej.

1. Proste miary zagrożenia

Najprostszym przykładem miar zagrożenia jest semiodchylenie standardowe. Jest to miara wywodząca się bezpośrednio bierze pod uwagę tylko negatywne sytuacje panujące na rynku. Formalnie przedstawia ze zwykłego odchylenia standardowego jednakże się ją następująco:

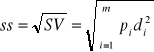
lub w przypadku odchylenia z próby

 

 

 

        Semiodchylenie standardowe interpretowane jest podobnie jak odchylenie standardowe. Jest to po prostu średnie odchylenie od średniej stopy zwrotu, ale w tym przypadku tylko stóp zwrotu mniejszych od średniej.

Bardzo podobną miarą jest semiodchylenie przeciętne.

Kolejną miarą zagrożenie jest poziom bezpieczeństwa. Definiuje się ją według następującego wzoru:

 

gdzie:

R_q - poziom bezpieczeństwa, wyrażany w procentach wartości stopy zwrotu

P( ) - prawdopodobieństwo zdarzenia

R - stopa zwrotu

α - ustalona wartość prawdopodobieństwa bliska wartości 0.

Poziom bezpieczeństwa jest to więc taka wartość stopy zwrotu, że osiągnięcie mniejszej od niej wartości jest bardzo mało prawdopodobne.

Alternatywnie poziom bezpieczeństwa możemy zapisać jako:

   

            Miara ta oznacza, że prawdopodobieństwo tego, że stopa zwrotu będzie większa od założonego poziomu bezpieczeństwa jest równe prawie 1 (zakładamy, że α jest bliskie 0). Oznacza to również, że jest bardzo mała szansa, że stopa zwrotu spadnie poniżej poziomu założonego. Jeżeli więc wartość poziomu bezpieczeństwa rośnie, to zmniejsza się wartość prawdopodobieństwa i ryzyko rośnie. Taka forma zapisu powyższej miary jest często określana jako poziom ufności (safety level).

Drugą z prostych miar zagrożenia jest prawdopodobieństwo nieosiągnięcia poziomu aspiracji (aspiration level). Określone jest ono za pomocą następującej relacji: 

Zauważmy, że z kolei w tym przypadku Pa jest niczym innym jak wartością dystrybuanty rozkładu prawdopodobieństwa zmiennej losowej opisującej stopy zwrotu dla argumentu Ra. Im wartość Pa mniejsza - tym lepiej.

2. Value-at-risk - wartość narażona na ryzyko - definicja

VaR można zdefiniować jako maksymalną stratę rynkowej wartości portfela lub instrumentu finansowego możliwą do poniesienia w konkretnym horyzoncie czasowym i przy założonym poziomie ufności.

Do obliczania VaR została opracowana specjalna metodologia zarządzania ryzykiem zwana RiskMetrics w 1994 r. przez firmę J.P. Morgan. Jest to najpopularniejsza metoda stosowana do pomiaru ryzyka rynkowego, jednak jest używana także do innych rodzajów ryzyka finansowego (operacyjnego i kredytowego). Stanowi podstawę dla takich miar zagrożenia jak np.: EaR (Earnings at Risk), LaR (Liquidity at Risk), EPSaR (Earnings Per Share at Risk), CCFaR (Credit Cash Flow at Risk), CFaR (Cash Flow at Risk).

Stosowanie miary Value at Risk wiąże się z szeregiem korzyści do których m.in. można zaliczyć takie aspekty jak:

• VaR stwarza możliwość formułowania różnych rodzajów ryzyka w sposób jednolity;

• W sposób nieskomplikowany dokonuje interpretacji;

• Uwzględnia dywersyfikację portfela;

• Posiadając odpowiednie dane dotyczące zrealizowanych strat, które przekraczają poziom VaR można w stosunkowo prosty sposób dokonać weryfikacji tej metody;

• Jest międzynarodowym standardem, rekomendowanym przez Komitet Bazylejski ds. Nadzoru Bankowego, Grupę Trzydziestu a w Polsce przez Generalny Inspektorat Nadzoru Bankowego (GINB);

• Ma swoje zastosowanie przy charakteryzowaniu rodzajów zabezpieczenia kapitału instytucji finansowej.

Metoda VaR oprócz korzyści posiada także wady:

• W sytuacji gdy strata przewyższy wartość VaR przedsiębiorstwo nie posiada informacji o wysokości spodziewanej straty;

• Mogą mieć miejsce przypadki, w których niemożliwe będzie odróżnienie pod względem ryzyka portfeli, pomimo, że ich ryzyko będzie w oczywisty sposób odmienne;

• W przypadku dużych i złożonych portfeli mogą istnieć problemy z jej oszacowaniem;

• Otrzymywane wyniki są wrażliwe na metodę estymacji.

Wartość zagrożona VaR zależy od dwóch elementów, które w każdym przedsiębiorstwie powinny być ustalone przez zarząd firmy. Tymi parametrami są:

• Poziom tolerancji (przykładowo firma J. P. Morgan stosuje 0,05, a Komitet Bazylejski 0,01) - poziom tolerancji, który jest bliski 0 może być także zamiennie stosowany z poziomem ufności, stanowiącym różnicę pomiędzy 1 (100%) a poziomem tolerancji; gdy poziom tolerancji jest niższy (poziom ufności jest wyższy), to wartość VaR jest większa.

• Horyzont czasowy (banki komercyjne stosują 1 dzień, Komitet Bazylejski 10 dni, fundusze inwestycyjne oraz pewna część przedsiębiorstw 1 miesiąc) - im dłuższy będzie horyzont czasowy, tym wyższą wartość będzie osiągała VaR.

W związku z powyższym VaR można zapisać w postaci równania:

gdzie:

α - poziom tolerancji,

W - wartość portfela (instrumentu) na koniec okresu, definiowana jako zmienna losowa,

W₀ - obecna, aktualna wartość portfela (instrumentu).

Przykład 1:

Jeżeli czas trwania inwestycji jest równy 1 miesiąc, aktualna wartość tej inwestycji wynosi 1.500 zł, poziom tolerancji 0,05 (5%), a VaR 200 zł, to prawdopodobieństwo, że w ciągu tego miesiąca strata z inwestycji osiągnie bądź przekroczy 200 zł wynosi 5%, a więc wartość portfela w następnym miesiącu nie będzie mniejsza niż 1.300 zł z 95%-wą pewnością.

Z powyższego równania wynika, że VaR jest funkcją kwantyla rozkładu stopy zwrotu. Oznaczmy przez Wα kwantyl rozkładu wartości (ceny) instrumentu finansowego odpowiadający zadanemu poziomowi tolerancji (prawdopodobieństwu) α. Wówczas z definicji kwantyla otrzymujemy:

gdzie:

Często zamiast rozkładu wartości stosowany jest rozkład stóp zwrotu. Przy założeniu prostej kapitalizacji odsetek, kwantyl rozkładu stóp zwrotu dla zadanego poziomu tolerancji można wyznaczyć ze wzoru:

Stąd formuła na obliczenie VaR będzie wynosić:

Jak widać z powyższego wzoru, podstawową charakterystyką niezbędną dla obliczenia VaR jest kwantyl rozkładu stóp zwrotu. Jeśli założymy, że rozkład ten ma charakter rozkładu normalnego, wówczas kwantyl jest funkcją średniej i odchylenia standardowego stóp zwrotu:

gdzie:

R - wartość oczekiwana rozkładu stóp zwrotu

S - odchylenie standardowe rozkładu stóp zwrotu

μ_1-α - kwantyl standardowego rozkładu normalnego rzędu 1-α

Stąd VaR możemy zapisać w postaci:

Alternatywną koncepcją jest koncepcja logarytmicznej stopy zwrotu, czyli kapitalizacji ciągłej. Dla takiego założenia kwanty rozkładu wyznaczymy z następującej równości:

A stąd VaR będzie się równać:

Uwaga: Kwantylem rzędu p, gdzie 0 ≤ p ≤ 1, w rozkładzie empirycznym P_X zmiennej losowej X nazywamy każdą liczbę x_p, dla której spełnione są nierówności

oraz

W szczególności, kwantylem rzędu p jest taka wartość x_p zmiennej losowej, że wartości mniejsze lub równe od x_p są przyjmowane z prawdopodobieństwem co najmniej p, zaś wartości większe lub równe od x_p są przyjmowane z prawdopodobieństwem co najmniej 1-p.

VaR zakłada „mormalne” funkcjonowanie rynku. Pomiar ryzyka za jego pomocą daje poprawne wyniki tylko wtedy, kiedy na rynku nie zdarzają się sytuacje nietypowe, ekstremalne. (przykład odstępstwa: 19.10.1987 - spadek SP500 o 22,3 dziennej zmienności mierzonej odchyleniem standardowym).

VaR podaje prawdopodobieństwo, z jakim strata nie powinna przekroczyć zakładanego poziomu, ale nie mówi nic o możliwych wielkościach straty w sytuacjach ekstremalnych.

Straty banków podczas kryzysu sub-prime wynikały z nadmiernego przywiązania do modeli opartych na VaR opisującyh normalne stany rynku. W tym samym okresie straty wielu towarzystw ubezpieczeniowych były zdecydowanie mniejsze gdyż wykazywały one mniejsze zaufanie do modeli i regularnie prowadziły analizy sytuacji ekstremalnych.

3. Szczególne formy VaR

1. VaR bezwzględny i VaR względny.

Rozważmy stwierdzenie „jednodniowy VaR w 99-procentowym przedziale ufności wysosi 2 mln USD”. Oznacza ono, że jest 1% szans, że jutro nasza firma straci więcej niż 2 mln USD. Najgorszy wynik, jakiego możemy się spodziewać w perspektywie jednego (najbliższego) dnia, to strata 2 mln USD. Przez „najgorszy wynik” rozumiemy najgorszy wynik w 99-procentowym przedziale ufności. Jeszcze inaczej mówiąc, istnieje 99% szans, że jutro stracimy nie więcej niż 2 mln USD. Rodzi się jednak pytanie czy te 2 mln USD oznaczają stratę, czy wynik gorszy od oczekiwanego? Jeśli spodziewamy się zarobić 0,5 mln, a możemy stracić - w 99-procentowym przedziale ufności - 2 mln, to VaR wynosi 2 mln, czy 2,5 mln USD? Aby uniknąć takich wątpliwości rozróżniamy VaR bezwzględny (Absolute VaR) i VaR względny (Relative VaR).

VaR absolutny mówi, ile możemy stracić (o ile może spaść wartość portfela w stosunku do wartości obecnej). W naszym przykładzie VaR absolutny wynosi 2 mln USD. Liczymy go według wzoru:

VaRabsolutny =-Wr

W - wartość portfela

r - najgorsza stopa zwrotu (w danym okresie przetrzymania i poziomie ufności; r < 0)

Natomiast VaR względny mówi nam o tym, o ile może spaść wartość portfela względem

wartości oczekiwanej:

VaRwzględn = -W(r - μ)

μ - oczekiwana stopa zwrotu z portfela w danym okresie przetrzymania

W naszym przykładzie VaR względny wynosi 2,5 mln USD.

VaR absolutny jest łatwiejszy do policzenia (nie musimy znać oczekiwanej stopy zwrotu), dlatego stosuje się go częściej. W praktyce czasami nie rozróżnia się między dwoma rodzajami VaR. Wynika to stąd, że liczymy VaR najczęściej dla krótkich okresów, jak 1 dzień lub 10 dni. Zwykle w tak krótkim czasie oczekiwana stopa zwrotu jest na tyle mała w porównaniu do ryzyka, że można ją pominąć.

b) Incremental VaR - VaR obliczany jest na ogół dla całego portfela inwestycyjnego. Jednak na wartość VaR portfela wpływa VaR każdego z instrumentów wchodzących w jego skład. Wpływ danej pozycji na ryzyko całego portfela jest określany jako Incremental VaR:

VaR_{incremental, A} = VaR_P+A - VaR_P

gdzie:

VaRP+A - ryzyko portfela zawierającego pozycję A

VaRP - ryzyko portfela nie zawierającego pozycji A

Innymi słowy, Incremental VaR mówi nam, jaki wkład w ryzyko (mierzone przez VaR) portfela będzie miało dodanie danej pozycji. Incremental VaR zawsze musi być rozpatrywany

w kontekście konkretnego portfela, ponieważ ta sama pozycja będzie miała różny Incremental

VaR w różnych portfelach. Incremental VaR może mieć nawet wartość ujemną, jeśli dana pozycja stanowi zabezpieczenie przed jednym z rodzajów ryzyka obecnych w portfelu. Przykładem pozycji o ujemnej wartości Incremental VaR jest krótka pozycja w kontraktach futures na indeks giełdowy dodana do portfela akcji jako jego zabezpieczenie przed ryzykiem rynkowym.

3. Component VaR

Component VaR mówi, o ile zmieni się VaR całego portfela, gdy usuniemy z portfela daną pozycję ma więc znaczenie bardzo zbliżone do Incremental VaR. Incremental VaR mówi bowiem o ryzyku pozycji, która nie jest częścią portfela, a Component VaR o ryzyku pozycji obecnej w portfelu. Każdy składnik portfela ma swój Component VaR, a suma Component VaR wszystkich instrumentów w portfelu daje VaR portfela:

Ze względu na podobieństwo definicji terminu Component VaR używa się często zamiennie z

Incremental VaR, przypisując im to samo znaczenie.

4. Marginal VaR (VaR krańcowy)

Marginal VaR mówi, jak zmieni się ryzyko portfela, gdy zwiększymy lub zmniejszymy kwotę zainwestowaną w dany instrument o jeden złoty. Z matematycznego punktu widzenia Marginal VaR jest pochodną VaR portfela po udziale instrumentu w portfelu:

w_A - wartość pozycji A w portfelu, wyrażona w walucie (np. PLN)

Marginal VaR jest wielkością niemianowaną. Może być stosowany do przybliżenia Incremental VaR:

Przykład:

Zastanawiamy się nad kupnem akcji pewnej spółki za 10 mln USD i chcemy znać ryzyko związane z tą pozycją. Policzenie Incremental VaR może zająć zbyt dużo czasu (za dużo jak na tak skromną inwestycję). Znajdujemy Marginal Var (np. 0,03) i mnożymy przez kwotę, którą chcemy zainwestować: 0,03 * 10 mln USD = 0,3 mln USD. W ten sposób znaleźliśmy przybliżony Incremental VaR. Marginal VaR jest wartością niemianowaną, ale - jak każdy inny VaR - jest określony dla danego poziomu ufności i okresu.

5. Individual VaR

Individual VaR określa ryzyko danej pozycji bez rozpatrywania korzyści płynących z dywersyfikacji. Individual VaR mówi, ile wynosi ryzyko portfela składającego się tylko z tej jednej pozycji. Jest wyższy od spokrewnionego z nim Component VaR, ponieważ nie bierze pod uwagę wpływu dywersyfikacji (jak wiemy, dywersyfikacja zmniejsza ryzyko). I tak, na przykład, przy przeprowadzaniu arbitrażu każda pozycja ma większy od zera Individual VaR (Individual VaR zawsze jest dodatni) i zerowy Component VaR. Obie miary są równe tylko w

jednej sytuacji: gdy wszystkie korelacje między składnikami portfela są równe 1.

Graficzną interpretację opisanych powyżej form VaR przedstawia wykres 1:

4. Metody szacowania VaR

VaR może być szacowany za pomocą kilku metod. Najczęściej stosowane są 3 metody szacowania VaR:

1. symulacja historyczna,

2. modele parametryczne,

3. symulacja Monte Carlo.

Ad 1) Najprostszą - i czasami najlepszą - metodą liczenia VaR jest symulacja historyczna.

Metoda ta składa się z następujących kroków:

1) ustalenie obecnej wartości portfela

2) zebranie danych o historycznych stopach zwrotu z identycznego portfela

3) znalezienie VaR przez pomnożenie obecnej wartości portfela i stopy zwrotu odpowiadającej przyjętemu poziomowi ufności.

Załóżmy, że chcemy poznać jednodniowy VaR w 95-procentowym przedziale ufności. Znamy obecny skład portfela i możemy sprawdzić, jak zmieniłaby się jego wartość w ciągu interesującego nas okresu przetrzymania (w naszym przykładzie jeden dzień), zaczynającego się np. rok temu. Znajdujemy informacje sprzed roku i patrzymy, jak zmieniłaby się wartość portfela, gdyby jutro powtórzyły się tamte zmiany cen. Tę samą operację powtarzamy dla danych z dnia następnego po dniu, który był rok temu. Otrzymujemy inną wartość. Powtarzamy wszystkie obliczenia dla zmian z kolejnych dni, aż do danych z wczoraj. Ponieważ interesował nas okres jednego dnia, a w ciągu roku na giełdzie jest około 250 takich okresów, mamy zbiór 250 zmian wartości portfela. Porządkujemy te obserwacje od najniższej do najwyższej. Chcemy znaleźć VaR w 95-procentowym przedziale ufności,

więc szukamy takiej wartości, poniżej której znajduje się 5% obserwacji. W naszym przykładzie trzynasta najniższa obserwacja stanowi szukany VaR. Oczywiście, nie musimy korzystać z danych z jednego roku. Decyzja o ilości użytych obserwacji zależy od nas. Musimy jednak pamiętać o wadach długiego i krótkiego okresu. Zbyt długi badany okres będzie zawierał sytuacje, które są obecnie bardzo mało prawdopodobne, gdyż sytuacja na rynku poważnie się zmieniła (korelacje i zmienności są zupełnie inne niż kiedyś). Z drugiej strony, krótki okres może nie objąć wyjątkowych zdarzeń, bardzo ważnych dla zarządzania ryzykiem. Na przykład, w krótkim czasie mogło nie dojść do żadnego załamania kursu krajowej waluty. Badany okres mógł być po prostu wyjątkowo spokojny.

W przypadku liczenia wartości narażonej na ryzyko w czasie dłuższym niż jeden dzień, np. VaR dziesięciodniowego, dramatycznie spada liczba dostępnych obserwacji: w ciągu roku, zamiast 250, mamy ich tylko 25. Możemy sztucznie zwiększyć liczbę obserwacji, jeśli pozwolimy, żeby kolejne dziesięciodniowe okresy na siebie zachodziły (tzw. overlapping periods). Niestety, ten sposób nie wniesie niczego nowego do naszej analizy, ponieważ częstość występowania np. załamań giełdowych zostanie ta sama. Nie zwiększymy ilości posiadanych informacji. W praktyce, zamiast liczyć VaR na podstawie dziesięciodniowych okresów przetrzymania, często szuka się jednodniowego VaR (używając jednodniowych okresów), po czym przeskalowuje się go wykorzystując zasadę pierwiastka kwadratowego czasu.

Ad. 2. Przykładem modelu parametrycznego obliczania wartości VaR jest metoda wariancji/kowariancji. Wywodzi się ona z definicji VaR jako funkcji kwantyla przyjętego rozkładu teoretycznego stóp zwrotu. Najczęściej stosowanym rozkładem jest rozkład Normalny, który jest całkowicie opisany tylko przez dwa parametry, średnią (
) i odchylenie standardowe (
). W takim wypadku wartość VaR wyznacza się z poniższej zależności:

gdzie:

- średnia rozkładu stopy zwrotu,

- odchylenie standardowe rozkładu stopy zwrotu,

c - stała zależąca od prawdopodobieństwa takiego, że:

1. Jeśli poziom ufności
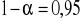
   to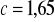
   

2. Jeśli poziom ufności
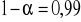
   to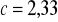
   

W przypadku większej liczby dni (dłuższe okresy) VaR obliczamy poprzez pomnożenie jednodniowego VaR przez pierwiastek kwadratowy z liczby dni dla których są przeprowadzane wyliczenia.

Ogromną zaletą tej metody jest jej prostota. Jednak w przypadku posiadania danych z przeszłości problemem może się okazać oszacowanie wariancji oraz średniej.

Ad 3. Symulacja Monte Carlo - należy przyjąć pewien zakładany, hipotetyczny model, który najdokładniej odzwierciedla sposób kształtowania się cen bądź stóp zwrotu instrumentów finansowych. Model ten powinien zostać zweryfikowany uprzednio na podstawie wielu danych empirycznych. Aby otrzymać rozkład stóp zwrotu portfela należy wygenerować bardzo dużo (np. kilka tysięcy) obserwacji stóp zwrotu (cen) instrumentów finansowych. Określenie VaR jest możliwe po wyznaczeniu kwartyla tego rozkładu. Metodę Monte Carlo stosuje się wtedy, gdy nie można wykorzystać innych podejść. Jest ona bardzo dokładna, jednak otrzymane wyniki w dużym stopniu zależą od przyjętego modelu stóp zwrotu (cen).

12

---