METODY UWZGLĘDNIANIA RYZYKA W RACHUNKU OPŁACALNOŚCI PROJEKTU INWESTYCYJNEGO

Ryzyko może być uwzględnione w kryteriach decyzyjnych:

• Bezpośrednio:

• uwzględnianie ryzyka w przewidywanych przepływach pieniężnych uzyskiwanych w całym okresie życia projektu - równoważnik pewności „a” (certaintly equivalent factor) - definiowany jako wartość otrzymana z pewnością, która ma tę samą użyteczność, co wartość oczekiwana niepewnej wartości,

• korygowanie wartości stopy dyskonta poprzez zastosowanie tzw. stopy dyskonta uwzględniającej ryzyko (risk - adjusted discount rate),

• podejście probabilistyczne - współczynnik zmienności (CV_NPV) oparty na wartości oczekiwanej i odchyleniu standardowym.

• Pośrednio:

Są to metody szacowania ryzyka, które wykorzystywane są w metodach bezpośrednich, i służą uzyskiwaniu informacji (tzn. zmniejszania niepewności) o projekcie. Ich znaczenie jest duże, gdyż umożliwiają dokładniejszą analizę projektów. Do metod tych należą:

• analiza wrażliwości (sensitivity analysis lub „what if analysis”),

• analiza scenariuszy (scenario analysis),

• analiza symulacyjna Monte Carlo (simulation analysis).

STOPA DYSKONTOWA UWZGLĘDNIAJĄCA RYZYKO

Stopa dyskontowa uwzględniająca ryzyko jest równa wymaganej stopie zwrotu projektu, uwzględniającej skalę ryzyka.

W praktyce są stosowane na ogół w tym zakresie dwa rozwiązania:

• rozwiązania subiektywne.

• rozwiązanie obiektywne (współczynnik zmienności CV)

Rozwiązanie subiektywne polega na wyodrębnieniu przez zarządzającego różnych klas ryzyka i przypisaniu do nich wyodrębnionych grup rodzajowych projektów inwestycyjnych.

Klasa ryzyka	Charakter projektu	Premia za ryzyko w %
I	odtworzeniowe	0
II	modernizacyjne	1
III	rozwojowe
III a	w obecnej branży	2,2
III b	w podobnej branży	3
III c	w zupełnie innej branży	od 5

EKWIWALENT PEWNOŚCI

W roku 1966 Alexander Robishek oraz Steward Myers opracowali propozycję stanowiącą alternatywne rozwiązanie dla metody uwzględniającej ryzyko w stopie dyskontowej. Ich rozumowanie opierało się na założeniu, iż skoro w celu uwzględnienia ryzyka możemy modyfikować stopę dyskontową, możliwe jest w tym celu również modyfikowanie oszacowanego strumienia wpływów i wydatków pieniężnych. Zgodnie z tym założeniem opracowali metodę, którą określamy mianem ekwiwalentu pewności. W literaturze anglojęzycznej jest ona znana pod nazwą Certainly Equivalent Adjustment (CEA).

Ekwiwalent pewności to kwota, jaką chcielibyśmy w przyszłości uzyskać ze 100% pewnością, jest ona równa oferowanej nam kwocie, większej co do wartości, ale co do której nie istnieje pewność czy ją otrzymamy.

Przykładowo, jeżeli jest nam wszystko jedno czy za rok otrzymamy 800 tys. zł ze 100% pewnością, czy też prawdopodobnie 1 mln zł, wówczas 800 tys. zł stanowi ekwiwalent pewności dla 1 mln zł. Innymi słowy w tym przypadku "bezryzykowne" 800 tys. zł jest w odczuciu inwestora warte tyle samo co "ryzykowne" 1 mln zł. Jeżeli wzrasta niepewność czy dany przypływ pieniądza rzeczywiście nastąpi w przyszłości, zmniejsza się dla danej kwoty ekwiwalent pewności. Tak więc wzrostowi ryzyka towarzyszy zmniejszanie się ekwiwalentu pewności.

Relacja między przepływem pieniądza a ekwiwalentem pewności przedstawia się w następujący sposób.

Cash Flow wolny od ryzyka (ekwiwalent pewności) = a_t Cash Flow "ryzykowny"

gdzie parametr a_t jest określany nazwą czynnika ekwiwalentu pewności dla przepływu gotówki, jaki ma nastąpić w czasie t.

Po przemnożeniu "ryzykownego" przepływu gotówki przez czynnik ekwiwalentu pewności otrzymujemy wielkość ekwiwalentu pewności dla danego przepływu.

Dla uwzględnienia ryzyka w analizie projektu inwestycyjnego poprzez zastosowanie opisywanej metody, każdy z przewidywanych Cash Flow, musi być przemnożony przez odpowiedni czynnik ekwiwalentu pewności. Ponieważ ryzyko uwzględniamy przez redukcję oczekiwanego Cash Flow, strumień pieniądza charakteryzujący projekt jest dyskontowany przy zastosowaniu stopy dyskontowej wolnej od ryzyka.

Jeżeli jesteśmy pewni wysokości rzeczywistego nakładu inwestycyjnego, który będzie poniesiony na koniec roku 0, wówczas ekwiwalent pewności dla tego wydatku a₀ = 1,0. W tym przypadku w kalkulacji NPV jest uwzględniany rzeczywisty nakład inwestycyjny.

Dla przypływów gotówki następujących w kolejnych latach, czynnik ekwiwalentu pewności przybiera wartości w przedziale (0; 1,0). Jeżeli jednak nakład inwestycyjny jest również ryzykowny (tzn. nie jesteśmy pewni jego wysokości), wówczas czynnik ekwiwalentu pewności (a₀) jest większy od jedności.

ANALIZA WRAŻLIWOŚCI

W ramach analizy wrażliwości mierzone są zmiany w wysokości NPV spowodowane określoną w procentach zmianą innych zmiennych. Czym bardziej "stromy" (większy) kąt nachylenia linii określającej wrażliwość, tym większa wrażliwość NPV na zmiany określonego parametru.

Analiza wrażliwości może być stosowana nie tylko do badania wrażliwości NPV, ale również do innych miar stosowanych jako kryterium przy podejmowaniu decyzji inwestycyjnych, jak IRR. Wrażliwość może być przy tym badana względem różnych zmiennych, np. występujących w prognozie ilości sprzedanych wyrobów, cen, kosztów, regulacji po­datkowych itd.

Najistotniejszą zaletą tego typu analizy jest możliwość wyodrębnienia wpływu jednej zmien­nej na efektywność analizowanej inwestycji. Umożliwia to znalezienie kluczowych czynni­ków, które w głównej mierze wywierają wpływ na uzyskany rezultat. Konkluzja ta jest wskazówką dla oceniającego projekt, na które elementy prognozy Cash Flow należy zwrócić szczególną uwagę.

Chociaż analiza wrażliwości jest jedną z najczęściej stosowanych metod analizy ryzyka projektu inwestycyjnego, ma ona także kilka istotnych ograniczeń. Pozwala co prawda wskazać te czynniki, na które najbardziej wrażliwa jest NPV projektu, jednak nie uwzględnia zakresu zmian, jakim podlegać mogą wymienione czynniki.

Dla określenia ryzyka nie wystarczy więc znać wrażliwość NPV na zmiany poszczególnych czynników ale także zakres możliwych zmian każdego z czynników, najlepiej przy uwzględnieniu rozkładu prawdopodobieństwa.

Jedną z metod uwzględniających obydwa wymienione kryteria jest analiza scenariuszy.

ANALIZA SCENARIUSZY

Ta metoda uwzględniania ryzyka w rachunku opłacalności projektów inwestycyjnych opiera się na rezygnacji z deterministycznego podejścia (zakładającego obliczenie jednej wartości NCF dla każdego roku, przy założeniu, że prawdopodobieństwo jej wystąpienia wynosi 1 przy szacowaniu NCF danego projektu inwestycyjnego.

NCF w tej metodzie oblicza się w sposób probabilistyczny, tzn. określa się kilka możliwych wartości NCF dla każdego roku i przypisuje się im określone prawdopodobieństwo.

Podejście takie nazywane jest analizą scenariuszy.

Analiza scenariuszy - technika analizy ryzyka, w której porównuje się “złe” i “dobre” zestawy warunków z wartościami wyjściowymi.

Scenariusz pesymistyczny - analiza, w której wszystkie dane wejściowe są ustalone przy najgorszych rozsądnie przewidywanych wielkościach.

Scenariusz optymistyczny - analiza, w której wszystkie dane wyjściowe są ustalone na poziomie najlepszej, rozsądnie przewidywanej wysokości.

Sytuacja wyjściowa - analiza, w której wszystkie dane wyjściowe są ustalone na wysokości najbardziej prawdopodobnym.

WSPÓŁCZYNNIK ZMIENNOŚCI

Przeprowadzenie oceny opłacalności projektu inwestycyjnego na podstawie metody probabilistycznej wymaga zastosowania podstawowych mierników statystycznych takich jak wartość oczekiwana, odchylenie standardowe czy współczynnik zmienności.

• Wartość oczekiwana NPV (E_NPV) = ;

• Odchylenie standardowe NPV () = ;

• Współczynnik zmienności (CV_NPV) = ;

Pojedynczy projekt będzie opłacalny, jeżeli wartość oczekiwana NPV będzie większa od zera (E_NPV 0).

O skali związanego z nim ryzyka świadczy poziom odchylenia standardowego NPV oraz współczynnika zmienności.

W przypadku porównywania dwóch projektów mogą wystąpić dwa podstawowe przypadki:

• wyższej wartości oczekiwanej NPV, towarzyszy niższe odchylenie standardowe (E_{NPV, A} > E_{NPV, B} i

σ _{NPV, A} < σ _{NPV, B}) wybieramy projekt A,

• wyższej wartości oczekiwanej NPV, towarzyszy wyższe odchylenie standardowe (E_{NPV, A} > E_{NPV, B} i

σ _{NPV, A} > σ _{NPV, B}) oblicza się wówczas współczynnik zmienności i wybiera się projekt charakteryzujący się niższym współczynnikiem, ponieważ projekt ten gwarantuje wyższą rekompensatę ponoszonego ryzyka.

Współczynnik zmienności może posłużyć także do oszacowania premii ryzyka. Im wyższy współczynnik, tym wyższe ryzyko wiąże się z realizacją danego projektu.

Współczynnik zmienności		Premia ryzyka (punkty procentowe)	Stopa procentowa (%)
Od	Do
0.0 0.1 0.3 0.5 0.7 0.9 1.1	0.1 0.3 0.5 0.7 0.9 1.1 1.4	0 1 3 6 10 15 22	i i + 1 i + 3 i + 6 i + 10 i + 15 i + 22

i - stopa procentowa odzwierciedlająca rentowność lokat pozbawionych ryzyka np. rentowność bonów skarbowych 52 tygodniowych.

Przykład:

Dla pewnego projektu inwestycyjnego przewiduje się 3 możliwe warianty kształtowania się wielkości sprzedaży i ceny.

Scenariusz	Prawdopodobieństwo wystąpienia (Pi)	Wielkość sprzedaży	Cena sprzedaży
Najgorszy	0,25	15000	1,5
Bazowy	0,5	20000	2
Najlepszy	0,25	25000	2,5

Odpowiednie tablice przepływów są zaprezentowane poniżej. Obliczyć wartość oczekiwana NPV, odchylenie standardowe oraz współczynnik zmienności.

Wariant pesymistyczny:

	Lata
	1992	1993	1994	1995	1996
Budynek	-12 000,00
Wyposażenie	-8 000,00
Wzrost NWC	-6 000,00				6 000,00
Sprzedaż		22 500,00	22 500,00	22 500,00	22 500,00
Koszty zmienne		13 500,00	13 500,00	13 500,00	13 500,00
Koszty stałe		5 000,00	5 000,00	5 000,00	5 000,00
Amortyzacja (budynek) - 2,5%		300,00	300,00	300,00	300,00
Amortyzacja (wyposażenie) 20%		1 600,00	1 600,00	1 600,00	1 600,00
Zysk brutto		2 100,00	2 100,00	2 100,00	2 100,00
Podatek (40%)		840,00	840,00	840,00	840,00
Zysk netto		1 260,00	1 260,00	1 260,00	1 260,00
Dodać amortyzację		3 160,00	3 160,00	3 160,00	3 160,00
Wartość umorzeniowa netto					10 660,00
Przepływy środków pieniężnych	-26 000,00	3 160,00	3 160,00	3 160,00	19 820,00
COt = 12%	1	0,8929	0,7972	0,7118	0,6355
	-26 000,00	2 821,56	2 519,15	2 249,29	12 595,61
NPV	-5 814,39
			Wartość umorzeniowa netto
			Budynek	Wyposażenie
Koszt nabycia			12000	8000
Wartość umorzeniowa (księgowa)*			10800	1600
Zakumulowana amortyzacja			1200	6400
Wartość umorzeniowa (rynkowa)			7500	2000
Zysk (strata na sprzedaży)			-3300	400
Podatek (40%)			-1320	160
Wartość umorzeniowa netto**			8820	1840
Razem				10660
* Wartość początkowa - zakumulowana amortyzacja
** Wartość umorzeniowa (rynkowa) - podatek

Wariant optymistyczny:

	Lata
	1992	1993	1994	1995	1996
Budynek	-12 000,00
Wyposażenie	-8 000,00
Wzrost NWC	-6 000,00				6 000,00
Sprzedaż		62 500,00	62 500,00	62 500,00	62 500,00
Koszty zmienne		37 500,00	37 500,00	37 500,00	37 500,00
Koszty stałe		5 000,00	5 000,00	5 000,00	5 000,00
Amortyzacja (budynek) - 2,5%		300,00	300,00	300,00	300,00
Amortyzacja (wyposażenie) 20%		1 600,00	1 600,00	1 600,00	1 600,00
Zysk brutto		18 100,00	18 100,00	18 100,00	18 100,00
Podatek (40%)		7 240,00	7 240,00	7 240,00	7 240,00
Zysk netto		10 860,00	10 860,00	10 860,00	10 860,00
Dodać amortyzację		12 760,00	12 760,00	12 760,00	12 760,00
Wartość umorzeniowa netto					10 660,00
Przepływy środków pieniężnych	-26 000,00	12 760,00	12 760,00	12 760,00	29 420,00
COt = 12%	1	0,8929	0,7972	0,7118	0,6355
	-26 000,00	11 393,40	10 172,27	9 082,57	18 696,41
NPV	23 344,65
				Wartość umorzeniowa netto
				Budynek	Wyposażenie
	Koszt nabycia			12000	8000
	Wartość umorzeniowa (księgowa)*			10800	1600
	Zakumulowana amortyzacja			1200	6400
	Wartość umorzeniowa (rynkowa)			7500	2000
	Zysk (strata na sprzedaży)			-3300	400
	Podatek (40%)			-1320	160
	Wartość umorzeniowa netto**			8820	1840
	Razem				10660
	* Wartość początkowa - zakumulowana amortyzacja
	** Wartość umorzeniowa (rynkowa) - podatek

Wariant wyjściowy:

	Lata
	1992	1993	1994	1995	1996
Budynek	-12 000,00
Wyposażenie	-8 000,00
Wzrost NWC	-6 000,00				6 000,00
Sprzedaż		40 000,00	40 000,00	40 000,00	40 000,00
Koszty zmienne		24 000,00	24 000,00	24 000,00	24 000,00
Koszty stałe		5 000,00	5 000,00	5 000,00	5 000,00
Amortyzacja (budynek) - 2,5%		300,00	300,00	300,00	300,00
Amortyzacja (wyposażenie) 20%		1 600,00	1 600,00	1 600,00	1 600,00
Zysk brutto		9 100,00	9 100,00	9 100,00	9 100,00
Podatek (40%)		3 640,00	3 640,00	3 640,00	3 640,00
Zysk netto		5 460,00	5 460,00	5 460,00	5 460,00
Dodać amortyzację		7 360,00	7 360,00	7 360,00	7 360,00
Wartość umorzeniowa netto					10 660,00
Przepływy środków pieniężnych	-26 000,00	7 360,00	7 360,00	7 360,00	24 020,00
COt = 12%	1	0,8929	0,7972	0,7118	0,6355
	-26 000,00	6 571,74	5 867,39	5 238,85	15 264,71
NPV	6 942,69
IRR	21,78%
				Wartość umorzeniowa netto
				Budynek	Wyposażenie
	Koszt nabycia			12000	8000
	Wartość umorzeniowa (księgowa)*			10800	1600
	Zakumulowana amortyzacja			1200	6400
	Wartość umorzeniowa (rynkowa)			7500	2000
	Zysk (strata na sprzedaży)			-3300	400
	Podatek (40%)			-1320	160
	Wartość umorzeniowa netto**			8820	1840
	Razem				10660
	* Wartość początkowa - zakumulowana amortyzacja
	** Wartość umorzeniowa (rynkowa) - podatek

Scenariusz	Prawdopodobieństwo wystąpienia (Pi)	Wielkość sprzedaży	Cena sprzedaży	NPV i
Najgorszy	0,25	15000	1,5	-5 814,39
Bazowy	0,5	20000	2	6 942,69
Najlepszy	0,25	25000	2,5	23 344,65
	Oczekiwana NPV	7853,91
	Odchylenie standardowe	10349,47
	Współczynnik zmienności	1,3

Przy zastosowaniu tej metody zarządzający, poza wyliczeniem NPV opartym na wartościach oczekiwanych wpływów i wydatków wariantu bazowego dokonuje analizy projektu bazując na założeniu, iż sytuacja ułoży się dla niego we wszystkich aspektach bardzo niekorzystnie lub też bardzo korzystnie.

Istotną wadą tej techniki jest jednak to, iż uwzględnia ona jedynie trzy sytuacje bazową, najlepszą oraz najgorszą. Prawdopodobieństwo, że wszystkie aspekty projektu przyjmą jednocześnie ekstremalne wartości (najlepsze lub najgorsze), nie jest jednak zazwyczaj duże. W rzeczywistości więc na ogół NPV przybierać może nie tylko trzy możliwe stany, ale znacznie więcej. Ten aspekt ryzyka może z kolei być zbadany poprzez zastosowanie modeli symulacyjnych.

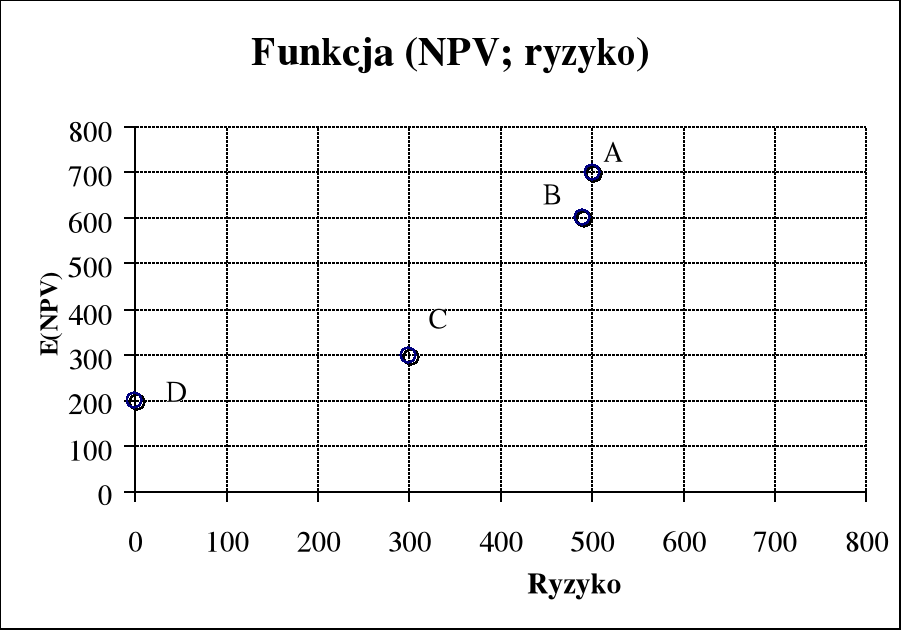
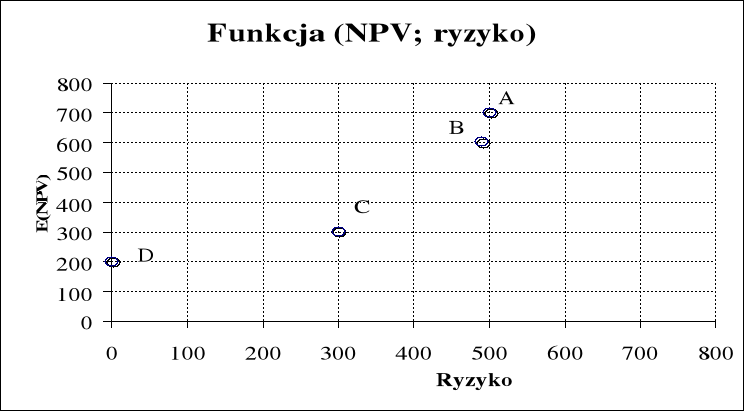
Wartość bieżąca netto nie jest miarą ryzyka projektu inwestycyjnego, przesądza ona jedynie o preferencji inwestora przy selekcji projektów inwestycyjnych. W praktyce preferowanie jednego projektu zamiast innego jest funkcją dwóch zmiennych: NPV i ryzyka. Można to przedstawić za pomocą poniższej formuły:

Preferencja = f (NPV, ryzyko) Przykład

	Wartość NPV		Prawdopodobieństwa
	WARIANT OPTYMISTYCZNY	WARIANT PESYMISTYCZNY	WARIANT OPTYMISTYCZNY	WARIANT PESYMISTYCZNY
Projekt
A	1200	200	0,5	0,5
B	1200	200	0,4	0,6
C	1200	200	0,1	0,9
D	1200	200	0	1
Projekt	Odchylenie standardowe	Wartość oczekiwana
A	500	700
B	490	600
C	300	300
D	0	200

Jeżeli wybierzemy do realizacji projekt A oznaczać to będzie, iż preferencją wyboru było przyjęcie najwyższej wartości oczekiwanej NPV, akceptując przy tym najwyższe ryzyko.

Do analizy tego przypadku przyjęliśmy założenie, iż wartość NPV może przybierać jedną z dwóch (lub trzech) wielkości. Dlatego też analizowany rozkład prawdopodobieństwa dotyczy wielkości dyskretnych, a więc ograniczonej ilości wariantów, jakie może przybrać NPV, przy czym każdemu z wariantów przypisana została odpowiadająca mu wartość prawdopodobieństwa. Jednak w wielu przypadkach trzeba przyjąć, iż NPV projektu może przybierać nieskończoną ilość wariantów. Rzeczywiście osiągnięty poziom NPV najczęściej może koncentrować się wokół wartości oczekiwanej NPV w taki sposób, że jego rozkład prawdopodobieństwa może być traktowany jako rozkład normalny mający kształt krzywej Gaussa której kształt wyznacza średnia (wartość oczekiwana) oraz odchylenie standardowe.

δ (NPV) δ (NPV)

E (NPV)

Rozkład normalny jest symetryczny, co ma duże znaczenie, ponieważ znany jest procent wszystkich możliwych wartości zmiennej leżących w oddaleniu od wartości oczekiwanej nie przekraczającym określonej wielokrotności odchylenia standardowego.

Na podstawie znajomości rozkładu normalnego nie jesteśmy jednak w stanie określić prawdopodobieństwa, że NPV przybierze założoną wartość, jednak możemy określić prawdopodobieństwo, iż NPV znajdzie się w określonym przedziale wartości.

Procent obszaru pod krzywą	99,73%	99,00%	95,45%	95%	90%	68%
Ilość odchyleń standardowych	3,00	2,58	2,00	1,96	1,65	1,00

99,73% wszystkich możliwych wartości NPV leży w przedziale [E(NPV) - 3δ; E(NPV) + 3δ]

68,27% wszystkich możliwych wartości NPV leży w przedziale [E(NPV) - 1δ; E(NPV) + 1δ]

Przykład

Jeżeli więc wiemy, że rozkład normalny NPV projektu A charakteryzuje się następującymi parametrami wartość oczekiwana 700 odchylenie standardowe 500, wiemy iż 68,27% wszystkich możliwych wartości NPV leży w przedziale: [200 ; 1200].

Bardzo ważną informacją jest określenie prawdopodobieństwa zaistnienia zdarzenia, polegającego na tym, że NPV inwestycji będzie wynosiła określoną wartość (np. będzie mniejsza od zera, a więc prawdopodobieństwo tego, że projekt okaże się nieopłacalny dla inwestora). W tym przypadku stosowana jest forma zestandaryzowanego rozkładu normalnego, dla którego za pomocą standaryzacji szacowana jest nowa wartość zmiennej Z.

NPV- E(NPV)

Z =

δ

Zmienna zestandaryzowana Z ma rozkład normalny o E(NPV) równej 0 i δ = 1. Tablice obszarów pod krzywą standaryzowanego rozkładu normalnego są publikowane, w związku z czym powierzchnię pod dowolną krzywą normalną można znaleźć przekształcając wartość zmiennej w wartość zestandaryzowaną Z i posługując się tablicami statystycznymi rozkładu zestandaryzowanego. Wartość Z informuje o ile odchyleń standardowych założona przez nas wartość jest odległa od wartości oczekiwanej NPV.

Wartość Z	Prawdopodobieństw, iż założony wynik jest bardziej odległy od wartości oczekiwanej
	0,5
0,1	0,4602
0,2	0,4207
0,3	0,3821
0,4	0,3446
0,5	0,3085
0,6	0,2743
0,7	0,242
0,8	0,2119
0,9	0,1841
1,0	0,1587
1,1	0,1357
1,2	0,1151
1,3	0,0968
1,4	0,0808
1,5	0,0668
1,6	0,0548
1,7	0,0446
1,8	0,0359
1,9	0,0287
2	0,0228
2,5	0,0062
3	0,0013
3,5	0,0002
4	0,00003

Dane te dotyczą tylko jednej strony wykresu rozkładu normalnego, czyli wielkości znajdujących się na „prawo” od wartości oczekiwanej

Przykład

Załóżmy, iż rozkład NPV dla projektu A jest rozkładem normalnym o parametrach: wartość oczekiwana 700 odchylenie standardowe 500.

Jakie jest prawdopodobieństwo, iż NPV będzie mniejsze od zera?

Krok 1

Obliczam wartość zestandaryzowaną Z wg wzoru

Wartość zmiennej - Wartość oczekiwana 0 - 700

Z = = = - 1,4

Odchylenie standardowe 500

W naszym przypadku odległość ta wynosi -1,4, co oznacza, iż NPV = 0, leży na wykresie po lewej stronie od wartości oczekiwanej NPV.

Informację należy odczytywać w sposób następujący: jeżeli dla Z = 1,4 odpowiadająca mu wielkość prawdopodobieństwa wynosi 0,0808, to 8,08% wynosi prawdopodobieństwo dla Z = -1,4 (czyli NPV mniejsze < E(NPV) - 1,4δ. Tak więc prawdopodobieństwo, iż dla danego projektu NPV < 0, wynosi 8,08%, zaś prawdopodobieństwo, iż NPV > 0 wynosi 1 - 0,0808 = 0,9192 tzn. 91,92%

Z = 1,4 Z = 0

NPV =0 E (NPV) = 700

---