III 12.01.04

Kolokwium 2

Zad.1. (8 p.) Rozwiąż równanie macierzowe AX = B, gdzie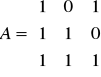
,
.

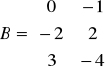
Zad. 2. (7 p.) Oblicz rząd macierzy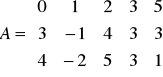
. Podaj przykład maksymalnego niezerowego minora tej macierzy.

Zad. 3. (12 p.) Przeprowadź dyskusję rozwiązalności następującego układu równań w zależności od wartości parametru a (tzn. zbadaj, dla jakich a układ jest oznaczony, dla jakich nieoznaczony, dla jakich sprzeczny).

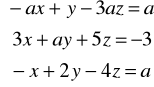
Zad. 4. (6p.) Wyznacz dwie różne bazy i wymiar przestrzeni liniowej
.

Zad. 5. (9 p.) Sformułuj definicję bazy przestrzeni liniowej. Wykaż, że wektory
tworzą bazę przestrzeni R². Wektor u ma w bazie
przestrzeni
współrzędne 2, 1 . Wyznacz współrzędne u w standardowej bazie przestrzeni
.

Zad. 6. (8 p.) Niech f : R⁴ → R² będzie przekształceniem liniowym określonym wzorem

f(x, y, z, t) = (2x + 3y + z + 2t, x+2y+3z). Wyznacz bazę jądra tego przekształcenia. Na tej podstawie oblicz wymiar Imf .

---