Konspekt wykładu 2 (A.Jóźwikowska)

ZBIORY

Zbiór liczb rzeczywistych z dołączonymi do niego symbolami
i
nazywamy

rozszerzonym zbiorem liczb rzeczywistych i oznaczamy
.

Przyjmujemy:

Jeżeli x jest liczba rzeczywistą

a)
,

,

.

b) Jeżeli
, to

.

c) Jeżeli
, to

.

Niech A będzie dowolnym niepustym podzbiorem zbioru R,
.

Zbiór A nazywamy ograniczonym z góry, jeżeli istnieje liczba M taka, że

.

Kresem górnym zbioru nazywamy najmniejsze z ograniczeń górnych tego zbioru.

Kres górny oznaczamy
, czytamy supremum A.

.

Dla zbioru nieograniczonego z góry przyjmujemy, że
.

Nie należy mylić kresu górnego zbioru z największą liczbą w zbiorze, którą -jeżeli istnieje-oznaczamy
. Oczywiście
istnieje wtedy i tylko wtedy, gdy
i wówczas

Analogicznie:

Zbiór A nazywamy ograniczonym z dołu, jeżeli istnieje liczba m taka, że

.

Kresem dolnym zbioru nazywamy największe z ograniczeń dolnych tego zbioru.

Kres dolny oznaczamy
, czytamy infimum A.

.

Własności kresu górnego

Jeśli
, to

a)
,

b) jeśli
, to w zbiorze A istnieje element większy od b,

c) jeśli
, to
.

Otoczeniem punktu
o promieniu r (
) nazywamy zbiór

Otoczeniem plus nieskończoności nazywamy przedział otwarty
, gdzie a jest dowolną liczbą.

Otoczeniem minus nieskończoności nazywamy przedział otwarty
, gdzie a jest dowolną liczbą.

Sąsiedztwem punktu
o promieniu r (
) nazywamy zbiór

Punkt a nazywamy punktem skupienia zbioru A, jeżeli w każdym sąsiedztwie punktu a istnieją punkty należące do zbioru A.

ILOCZYN KARTEZJAŃSKI

Niech A i B będą dowolnymi niepustymi zbiorami.

Iloczynem kartezjańskim
zbiorów A i B nazywamy zbiór par uporządkowanych
takich, że
i

Ciągi Liczbowe

Funkcję odwzorowującą zbiór liczb naturalnych N w zbiór liczb rzeczywistych R
nazywamy ciągiem liczbowym (nieskończonym) i oznaczamy
gdzie
.

Ciągi monotoniczne

Ciąg
jest

.

Ciągi ograniczone

Ciąg
jest:

Granica ciągu

Ciąg zbieżny do granicy skończonej

Def 1:

Liczbę g nazywamy granicą ciągu
, jeżeli spełniony jest warunek

.

dla dowolnej liczby dodatniej
istnieje liczba
taka, że wszystkie wyrazy ciągu o wskaźnikach większych od
różnią się od g mniej niż o
.

Zapisujemy
lub
.

Zwrot „Prawie wszystkie wyrazy ciągu” oznacza wszystkie wyrazu ciągu z wyjątkiem co najwyżej skończenie wielu.

Def 1a:

Liczbę g nazywamy granicą ciągu
, jeżeli w dowolnym otoczeniu liczby g leżą prawie wszystkie wyrazy tego ciągu.

Ciąg, który ma granicę (skończoną) nazywamy zbieżnym.

Zbieżność ciągu oznacza istnienie skończonej granicy tego ciągu.

Ciąg, który nie ma granicy skończonej nazywamy rozbieżnym.

Ciągi rozbieżne

Def 2:

Ciąg
nazywamy rozbieżnym do
jeżeli

dla dowolnej liczby A istnieje liczba
taka, że wszystkie wyrazy ciągu o wskaźnikach większych od
są większe od liczby A.

Def 3:

Ciąg
nazywamy rozbieżnym do
, jeżeli

Zapisujemy

lub
.

lub
.

Mówimy, że
, (
) jest granicą niewłaściwą ciągu.

Istnieją ciągi rozbieżne (czyli takie, które nie mają skończonej granicy), które nie są rozbieżne ani do
ani do
.

Przykład. Ciąg
jest rozbieżny.

Rachunek granic skończonych

Tw.

Jeżeli
i
, to

1.

2.

3.
przy założeniu, że
.

Tw. 1

Jeśli ciąg jest zbieżny, to ma dokładnie jedną granicę.

Tw. 2

Jeżeli ciąg jest zbieżny, to jest ograniczony.

Wniosek

Ciąg, który nie jest ograniczony jest ciągiem rozbieżnym.

Uwaga! Twierdzenie odwrotne nie zachodzi.

Ciąg ograniczony, może być ciągiem rozbieżnym.

Tw. 3

Jeżeli ciąg jest monotoniczny i ograniczony, to jest zbieżny.

Liczba Eulera e*2,718281...

Niech

Dowodzi się, że ciąg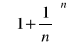
jest rosnący i ograniczony, a więc zbieżny.

Granicę tego ciągu oznaczamy literą e.

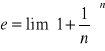
Można wykazać, że e jest liczbą niewymierną.
. Logarytm o podstawie e nazywamy logarytmem naturalnym i oznaczamy symbolem ln.

7

---