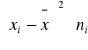Badano w 5 rodzinach :X ilość dzieci w rodzinie, Y wydatki związane z szkołą w setkach zł. Otrzymano następujące dane:

X	y
1 2 3 4 5	3 4 7 10 11

W jakim stopniu wydatki są uzależnione od liczby dzieci w rodzinie? Ile dzieci może mieć rodzina w której łącznie wydatki związane z szkołą mogą wynosić 600 zł?

Odpowiedź:

X	y
1 2 3 4 5	3 4 7 10 11	-2 -1 0 1 2	-4 -3 0 3 4	8 3 0 3 8	4 1 0 1 4	16 9 0 9 16
				22	10	50

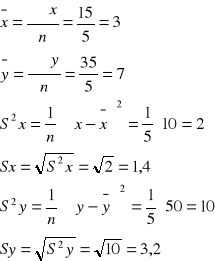
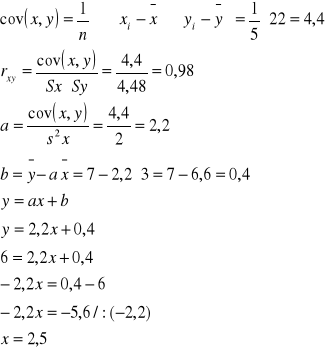
odpowiedź: Średnia ilość dzieci w rodzinie, w której wydatki na szkolnictwo wynoszą 600 zł wynosi 2,5. Czyli rodzina może mieć od 2 do 3 dzieci.

Liczba maszyn w 10 badanych gospodarstwach pewnej gminy wyniosła odpowiednio: 6,4,4,2,0,2,4,6,10,4. Jaka jest liczba maszyn w 25%, 50%, 75% rozpatrywanych gospodarstw? Jakie gospodarstwa przeważają : o liczbie maszyn przypadających na gospodarstwo: niższej czy wyższej od średniej?

Odpowiedź:

6,4,4,2,0,2,4,6,10,4

Q_{1 Me} Q₃

0,2,2,4,4,4,4,6,6,10

Me=4 jest to wartość środkowa przedziału

Q₁=2

Q₂=4

Q₃=6

odp. Liczba maszyn w gospodarstwie 25% wynosi 2, w 50% wynosi 4 a, w 75% wynosi 6. Liczba maszyn przypadająca na jedno gospodarstwo jest niższa od średniej, bo średnia jest większa od mediany i rozkład asymetrii jest prawostronny.

Zad. 3

Wartość produkcji artykułów A,B,C w latach 95 i 96 w mln zł i dynamikę ilości przedstawia poniższa tabela:

	Wartość produkcji w mln zł			Dynamika cen
Artykuł	1995r	1996r
A B C	10 20 50		Spadek o 20% Wzrost o 30% Wzrost o25%	Spadek o 10% Wzrost o 20% Bez zmian

Dokonać agregatowej analizy dynamiki produkcji artykułów A, B, C w celu łącznej oceny dynamiki obrotów w 1996r w porównaniu z 1995r.

Odpowiedź:

	ω0	ω1	Pp	ip
A B C	10 20 50	8 26 62,5	-10% 20% 0%	1,1 0,8 1	11 16 50	7,2 32,5 62,5

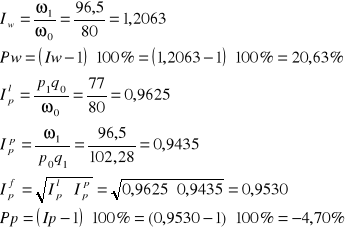
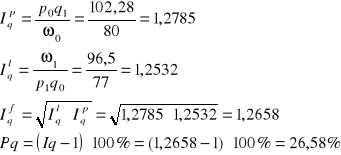
odp. Wzrost wartości o 20,63% spowodował spadek cen o 4,70% i spadek klientów, spadek ilości o 26,58%.

Zad. 4

W firmie Telimena zbadano 500płaszczy spośród nowo wyprodukowanej partii, otrzymano następujący rozkład usterek:

Liczba usterek	0	1	2	3	4	5
Liczba płaszczy	140	150	90	70	40	10

Wyznacz w oparciu o poziom ufności 0,90 przedziały ufności: dla przeciętnej liczby usterek i dla odchylenia standardowego liczy usterek w badanych płaszczach. Zbadaj precyzję oszacowania przedziałowego.

Odpowiedź:

0 1 2 3 4 5	140 150 90 70 40 10	0 150 180 210 160 50	315 37,5 22,5 157,5 170 122,5

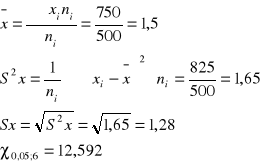
odp. Przeciętna liczba usterek wynosi 1,5; odchylenie standardowe wynosi 1,28; a precyzja oszacowania przedziałowego wynosi 12,592.

Zadania

1

www.wkuwanko.pl

---