POLITECHNIKA LUBELSKA w LUBLINIE
LABORATORIUM FIZYKI		Ćwicz. nr 2.1
TEMAT: Wyznaczanie zależności współczynnika załamania światła Od stężenia roztworu		DATA: 05.12.2000
WYKONAŁ: Tymoszyński Piotr	GRUPA: ED 3.7	OCENA:

KRÓTKA TEORIA:

Światłem w ujęciu optyki falowej nazywamy promieniowanie elektromagnetyczne emitowane z atomów i cząsteczek znajdujących się w stanie wzbudzonym. Zakres długości fal światła, na które reaguje oko ludzkie zawiera się w przedziale od λ_F=0.38 10^-6m. do λ_C=0.78 10^-6m. Dołączając do tego przedziału promieniowanie podczerwone i nadfioletowe, otrzymujemy pełen zakres tzw. promieniowania optycznego W oparciu o teorię światła można teoretycznie wyjaśnić zjawisko refrakcji.

Zjawisko refrakcji światła nazywamy w ogólności zachowanie się światła na granicy dwóch ośrodków o różnych własnościach optycznych. Nie wnikając szczegółowiej w naturę fizyczną tego zjawiska stwierdzamy że, promień świetlny na granicy dwóch ośrodków częściowo odbija się, a częściowo załamuje. Bardzo dokładne wyznaczenie wartości kąta α_g-(kąt graniczny), a co za tym idzie i współczynnika załamania ośrodka n, umożliwia przyrząd optyczny zwany refraktometrem. Spośród wielu typów refraktometrów, różniących się budową i działaniem, najczęściej używane są refraktometry Abbego.

Tabela wyników uzyskanych na laboratorium

C%	nD	n
				1	2	3
0	1,3328	1,3328	1,3328	1,3328
20	1,353567	1,3537	1,3534	1,3536
40	1,373233	1,3732	1,3733	1,3732
60	1,393867	1,3939	1,3939	1,3938
80	1,411867	1,4118	1,4119	1,4119
100	1,4302	1,4302	1,4301	1,4303

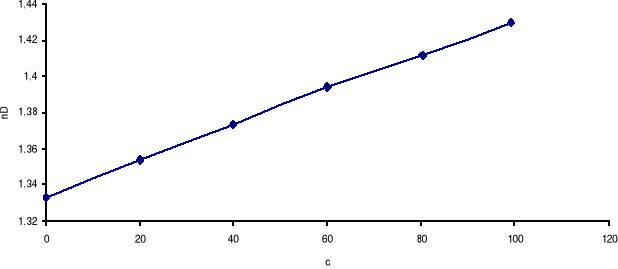
Wykres zależności n_D od stężenia roztworu C%

Tabela wyników uzyskanych na podstawie laboratorium

Lp	nD	z			1	2	3
	1,3625	41,5		nDśr	1,3626	1,3837	1,4027
	1,3629	41,8
1	1,3623	41,9		zśr	41,86	42	42,24
	1,3629	42
	1,3628	42,1		Cx%	30	50	70
	1,3839	42
	1,3839	41,8		A
2	1,3839	42,1
	1,3834	42		B
	1,3834	42,1
	1,4027	42,2		δ
	1,4028	42,6
	1,4028	42,3		T[K]	297,15	297,15	297,15
	1,4027	42,5
3	1,4028	42,4		ds.
	1,4029	42
	1,4028	42		dw
	1,4028	41,9
	1,4027	42
	1,4028	42,5

L.p	Xi	Yi	Xi^2	Xiyi	Wi	A	B
1	0,2	1,3547	0,04	0,27094	1	0,121	1,3328
2	0,4	1,3779	0,16	0,55116	1
3	0,6	1,4009	0,36	0,84054	1
4	0,8	1,4225	0,64	1,138	1
5	1	1,46286	1	1,46286	1
	Σxi=3	Σyi= 7,01886	Σxi^2= 2,2	Σxiyi= 4,2635	Σwi=5

D = = 1,222 y'=a*xi+b

a = = 0,121

L.p	xi	b	a	Yi	y'i	Δy	(Δy)^2	Wi
1	0,2	1,3328	0,121	1,3547	1,357	0,0023	0,000005	1
2	0,4					1,3779	1,3812	0,0033	0,00001	1
3	0,6					1,4009	1,4054	0,0045	0,00002	1
4	0,8					1,4225	1,4296	0,0071	0,00005	1
5	1					1,46286	1,4538	-0,009	0,000082	1
							Σ(Δy)^2= 0,000167	Σwi=5

∆a = = 0,015

∆b = = 0,01

równanie interesującej nas prostej zapiszemy następująco:

y = (a+-∆a)x + (b+-∆b)

współczynnik osłabienia promieniowania γ przez stal wynosi

u = |a| +-∆a

u = (0,121+-0,015)

błąd względny

δ_a = (0,015) / (0,121) = 0,1239 i procentowo δ_u = 12,39 %

δ_b=(0.01)/(1.3328)=0,0075 i procentowo 0,75%

1

2

---