Politechnika Śląska W Gliwicach Rok Akademicki 1998/99

Wydział Elektryczny Semestr IV Mgr

Laboratorium Elektrotechniki Grupa 1

CZWÓRNIK

REAKTANCYJNO-REZYSTANCYJNY

SEKCJA 4 :

1. Gorgolewski Mariusz

2. Kielerz Anna

3. Szopa Michał

4. Wójtowicz Jarosław

CEL ĆWICZENIA

Celem ćwiczenia jest zapoznanie się ze sposobem wyznaczania współczynników równań czwórnika w przypadku, gdy zawiera on elementy reaktancyjne i współczynniki równań są wielkościami zespolonymi, jak również zapoznanie się z wykorzystaniem tych współczynników do konstrukcji miejsc geometrycznych wielkości zaciskowych czwórnika.

UKŁADY POMIAROWE

Układ do wyznaczenia współczynnika a₁₂

Układ do wyznaczenia współczynnika a₂₁

Układ do wyznaczenia współczynników a₁₁ i a₂₂

Układ do wyznaczenia miejsc geometrycznych prądu

WYZNACZANIE WSPÓŁCZYNNIKÓW RÓWNANIA ŁAŃCUCHOWEGO

Tabele z danymi niezbędnymi do wykonania poniższych obliczeń znajdują się na załączonej do sprawozdania karcie pomiarowej. Obliczenia wykonano w układach pomiarowych oraz zgodnie z zależnościami podanymi w skrypcie.

współczynnik a₁₁ :

|a₁₁|=1,06

Arg a₁₁=31°

znak argumentu : „-”

a₁₁=1,06e^-j31°

współczynnik a₁₂ :

|a₁₂|=232,14 []

Arg a₁₂=23°

znak argumentu : „-”

a₁₂=232,14e^-j23°

współczynnik a₂₁ :

|a₂₁|=0,002 [S]

Arg a₂₁=81°

znak argumentu : „-”

a₂₁=0,002e^-j81°

współczynnik a₂₂ :

|a₂₂|=0,7 []

Arg a₂₂=13°

znak argumentu : „-”

a₂₂=0,7e^-j13°

W przypadku wyznaczenia wartości elementów a₁₁ i a₂₂ należało dokonać pewnych obliczeń pośrednich, których sposób przeprowadzenia został przedstawiony we wstępie teoretycznym do ćwiczenia w skrypcie.

Zatem macierz łańcuchowa badanego w przeprowadzonym ćwiczeniu czwórnika ma postać :

Wartości kątów argumentu liczby zespolonej Arg zostały zaokrąglone do pełnych stopni.

Sprawdzając otrzymane wartości elementów wykorzystamy zależność AD-BC=1.

AD-BC=1,05e^-j67°=0,42-j0,97

WYZNACZANIE MIEJSC GEOMETRYCZNYCH

Obliczenia teoretyczne zostały wykonane na podstawie przykładu obliczeniowego zamieszczonego w skrypcie.

Obciążenie Z=710e^j87°

W tym wypadku wartości I(0) oraz I() są takie same (niezależnie od włączonego w obwód pomiarowy kondensatora) i wynoszą odpowiednio :

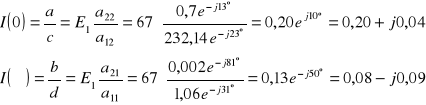
A kąt  ma wartość :

Jest to wartość równa w tym i we wszystkich pozostałych przypadkach zastosowanego obciążenia.

Dla układów z obciążeniem Z=1280e^j87° oraz obciążonym całością oraz połową baterii kondensatorów wartości I(0) oraz I() są praktycznie takie same (po zaokrągleniu do trzech cyfr znaczących po przecinku wartości są identyczne), więc w dalszej części sprawozdania wyniki obliczeń zostały pominięte.

WNIOSKI

W ćwiczeniu zajmowaliśmy się problematyką związaną z pomiarami parametrów czwórnika reaktancyjno-rezystancyjnego. Pierwszym etapem ćwiczenia było wyznaczenie współczynników równań czwórnika, gdy obwód zawiera elementy reaktancyjne, a otrzymane współczynniki są wielkościami zespolonymi. Dla wykonanych pomiarów uzyskaliśmy następujące wartości współczynników : a₁₁=1,06e^-j31°; a₁₂=232,14e^-j23°; a₂₁=0,002e^-j81°; a₂₂=0,7e^-j13°. W celu sprawdzenia poprawności otrzymanych wyników wykorzystaliśmy warunek, że różnica iloczynów odpowiednich par współczynników powinna być równa 1. Otrzymany wynik wprawdzie nieznacznie odbiega od założonej teoretycznie wartości, ale możemy uznać że współczynniki równań czwórnika są poprawne, gdyż na taki wynik mogły mieć wpływ błędy, jakimi są obarczone pomiary wykonywane przy użyciu mierników analogowych oraz błędy wprowadzone przez metodę pomiarową, błędy przypadkowe wynikające z chwilowego stanu energetycznego układu itp.

W ćwiczeniu wyznaczyliśmy także miejsca geometryczne prądu, których wykresy zamieszczamy w sprawozdaniu. Dla ustalonego napięcia na zaciskach wejściowych wielkości prądu wejściowego zależą od czterech współczynników równania łańcuchowego oraz od impedancji obciążenia. Jedynym ograniczeniem dla impedancji obciążenia przy jej pasywności jest fakt, że część rzeczywista impedancji nie może być ujemna, dlatego impedancja może przyjmować dowolne wartości z prawej pół płaszczyzny liczb zespolonych.

Miejscem geometrycznym impedancji wejściowej (przy zmianie obciążenia czwórnika) jest koło - jego wnętrze dla obciążeń rezystancyjno-reaktancyjnych, sam okrąg zaś dla obciążeń czysto reaktancyjnych. Jak wiadomo, nie istnieją idealne cewki (zawsze posiadają określoną rezystancję, co jest zresztą uwidocznione na tabliczce znamionowej cewek wykorzystywanych w ćwiczeniu), ani idealne kondensatory (każdy ma pewną upływność). Jest to jednym z powodów rozrzutu miejsc geometrycznych impedancji wejścia przy konkretnym (reaktancyjnym) obciążeniu wokół okręgu wyznaczonego analitycznie.

Kolejnym powodem wyżej wymienionej rozbieżności jest błąd metody wyznaczenia samego okręgu. Został wyznaczony na podstawie obliczonych drogą pomiarową współczynników macierzy łańcuchowej.

Znajomość miejsca geometrycznego jednej ze zmieniających się wraz z obciążeniem wielkości wejściowej (impedancja i prąd) lub wyjściowej (prąd) umożliwia nam dosyć dokładne oszacowanie zachowania się tej wielkości w pełnym zakresie zmian obciążenia.

Teoria czwórników pozwala na analizę obwodów bez znajomości dokładnej budowy niektórych elementów (właśnie czwórników). Znajomość pomiarowo wyznaczonych parametrów macierzy łańcuchowej umożliwia dokładny opis zachowania się elementu w obwodzie elektrycznym.

---