Teoria błędów
Przedmiot i cel rachunku wyrównawczego
Przedmiotem rachunku wyrównawczego są wartości pomiarów tj. spostrzeżeń wielkości geometrycznych. Z doświadczenia wiadomo, że spostrzeżenia te obarczone są błędami wynikającymi z różnych przyczyn. Dlatego też nie zadowala nas jedno spostrzeżenie, powtarzamy je dwa, kilka lub kilkanaście razy (są to tzw. spostrzeżenia nadliczbowe) w zależności od żądanej dokładności.
Celem rachunku wyrównawczego jest znalezienie spośród wszystkich wykonanych spostrzeżeń wartości najprawdopodobniejszej, czyli wyrównanej. Dalszym celem wyrównania jest określenie dokładności spostrzeżenia tak przed, jak i po wyrównaniu oraz często ustalenie metody pomiaru dla uzyskania z góry zadanej dokładności.
Rodzaje błędów
1. Błędy grube (omyłki, przeoczenia) mają zwykle dużą wartość liczbową i popełniane są wskutek braku należytej uwagi i staranności w czasie pracy. Przyczyną ich może być np. zgubiona szpilka miernicza, przy pomiarze długości taśmą, błędne odczytanie 9 zamiast 6, zapisanie 162 zamiast 126, błędy dwustugradowe przy odczytywaniu limbusa, błędy wielkości całych metrów lub dziesiątek gradów itp. Rachunek wyrównania nie zajmuje się tymi błędami. Po stwierdzeniu takiego błędu należy go usunąć przez powtórny pomiar kontrolny i to przed zastosowaniem metod rachunku wyrównania do wykonywanych spostrzeżeń.
2. Błędy systematyczne są to błędy mające swe źródło w otoczeniu (temperatura, refrakcja, oświetlenie), w fizycznie upośledzonym oku obserwatora lub w niedostatecznie sprawdzonym przyrządzie geodezyjnym (nominalna długość taśmy lub łaty nie jest zgodna z długością rzeczywistą, błędy w podziale limbusów). Mają one zatem w szczególnych przypadkach charakter stały i również powinny być przed wyrównaniem spostrzeżeń wyeliminowane przez wprowadzenie odpowiednio obliczonych poprawek do wyników pomiaru.
Błędy grube i systematyczne są błędami, których można uniknąć wykonując obserwacje z uwagą i sumiennością przy użyciu dobrych przyrządów. Nieuniknione są natomiast błędy następujące:
3. Błędy przypadkowe. Są to błędy małe, popełniane stale przy każdym spostrzeżeniu pomimo należytych starań i sumienności w pracy, z przyczyn nie dających się ustalić i mające z równym prawdopodobieństwem znak plus lub minus. Zadaniem rachunku wyrównania jest obliczenie takich poprawek do wykonanych spostrzeżeń, aby ich wielkości poprawione nie dawały odchyłek, czyli aby nie były sprzeczne z układami matematycznymi, którym spostrzeżenia te mają czynić zadość.
4. Błędy prawdziwe i błędy pozorne. Błąd prawdziwy ![]()
jest to różnica między wartością pomierzoną i wartością prawdziwą spostrzeżenia
![]()
,
gdzie ![]()
— wartość prawdziwa, L — wartość pomierzona.
W równaniu tym znana jest tylko wartość pomierzona L, a ponieważ wartość prawdziwa wielkości mierzonej bezpośrednio jest z reguły nieznana, zatem nie jest także znany błąd prawdziwy pojedynczego spostrzeżenia.
W praktyce geodezyjnej dążymy do uzyskania wartości najlepszych, tj. najbliższych wartości prawdziwej. Będzie to wartość wyrównana, czyli najprawdopodobniejsza.
Błąd pozorny spostrzeżenia — v jest to różnica między pomierzoną i wyrównaną wartością spostrzeżenia:
![]()
natomiast poprawka wyrównawcza v jest to wielkość równa błędowi pozornemu, lecz z przeciwnym znakiem, czyli wartość, którą należy dodać do spostrzeżenia, aby otrzymać jego wartość wyrównaną:
![]()
gdzie ![]()
— wartość wyrównana, L —wartość pomierzona.
Błędy, za pomocą których charakteryzuje się dokładność spostrzeżeń lub funkcji spostrzeżeń:
1. Błąd absolutny jest to błąd przypadający na całą nieznaną wielkość.
2. Błąd względny jest to błąd przypadający na jednostkę mierzonej wielkości, czyli stosunek błędu absolutnego do mierzonej wielkości.
Wyrażamy ten błąd zwykle za pomocą ułamka z jednością w liczniku lub za pomocą procentu i stosujemy tylko przy charakteryzowaniu dokładności pomiaru długości lub powierzchni, nie ma on natomiast zastosowania do charakterystyki pomiaru kąta lub różnic wysokości, ponieważ tu dokładność pomiaru nie zależy od wielkości mierzonych elementów.
3. Błąd średni pojedynczego spostrzeżenia obliczony na podstawie błędów prawdziwych ε. Wynosi on:
![]()
, (1)
gdzie n jest liczbą błędów prawdziwych, a więc i liczbą spostrzeżeń.
Wobec braku możliwości określenia błędów prawdziwych pojedynczych spostrzeżeń wzór ten jest rzadko stosowany. Niekiedy można określić błąd prawdziwy funkcji, np. różnica między sumą teoretyczną kątów w poligonie zamkniętym a sumą pomierzonych kątów jest błędem prawdziwym sumy pomierzonych kątów. Podobnie odchyłka zamknięcia różnic wysokości w zamkniętym ciągu niwelacyjnym jest błędem prawdziwym tego zamknięcia.
Średni błąd wyznaczenia kąta w sieci triangulacyjnej można obliczyć na podstawie błędów prawdziwych sum kątów w trójkątach wg wzoru Ferraro
![]()
, (2)
gdzie f - odchyłka zamknięcia kątów w poszczególnych trójkątach sieci, n - liczba trójkątów.
Należy odróżnić średni błąd pomiaru kąta, wyznaczony na podstawie wyrównań stacyjnych, od średniego błędu wyznaczenia kąta wg wzoru Ferrero. Ten ostatni jest przeważnie większy ze względu na to, że oprócz błędów popełnionych przy pomiarze kąta obejmuje on jeszcze błędy centrowania lub błędy wyznaczenia elementów mimośrodu, błędy środowiska, tj. błędy wynikające z różnych warunków pomiaru na różnych stanowiskach, błędy jednostronnego oświetlenia sygnałów itp.
3 a. Błąd średni pojedynczego spostrzeżenia przy wielokrotnych spostrzeżeniach jednej wielkości w przypadku, gdy błędy prawdziwe nie są znane, obliczamy na podstawie błędów pozornych z wzoru
![]()
. (3)
4. Błąd średni błędu średniego. Wzór (1) na błąd średni jest słuszny dla n zdążającego do nieskończoności, natomiast przy skończonej liczbie n spostrzeżeń otrzymujemy tylko przybliżoną wartość błędu średniego. Obliczony zatem z tego wzoru błąd średni będzie tym bliższy swej wartości prawdziwej, im większej liczby spostrzeżeń użyjemy do jego wyznaczenia, tj. im większe będzie n. Z rozważań tych nie należy w żadnym razie wyciągać wniosku, że w praktyce stale powinniśmy się starać o wykonanie jak największej liczby spostrzeżeń, trzeba tu bowiem zwrócić także uwagę na ekonomiczną stronę zagadnienia. Dokładność wartości wyrównanej uzyskana przez wielokrotne powtarzanie spostrzeżeń nie jest proporcjonalna do straty czasu i kosztów powtarzania prac obserwacyjnych, gdyż wzrost dokładności po osiągnięciu pewnej granicy powtarzania spostrzeżeń jest tak znikomy, że dalsze ich powtarzanie już się nie opłaca.
Można udowodnić, że błąd średni błędu średniego wyraża się wzorem
![]()
, (4)
jeżeli błąd średni m został obliczony na podstawie błędów prawdziwych, oraz wzorem
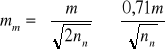
(5)
jeżeli błąd średni m został obliczony na podstawie błędów pozornych.
We wzorach (4) i (5) ![]()
jest błędem średnim błędu średniego, ![]()
jest liczbą spostrzeżeń nadliczbowych, tj. takich, które nie są niezbędne do jednoznacznego określenia wielkości wyznaczonych. Liczbę spostrzeżeń nadliczbowych określamy z wzoru
![]()
, (6)
gdzie n — liczba spostrzeżeń wykonanych, u — liczba spostrzeżeń niezbędnych do jednoznacznego określenia wielkości wyznaczanych.
W praktyce do oceny dokładności pomiarów lub wyznaczanych niewiadomych używamy zwykle błędów średnich.
5. Błąd graniczny ![]()
jest to błąd, którego prawdopodobieństwo przekroczenia jest praktycznie równe zeru. W praktyce przyjmuje się, że g znajduje się w przedziale
![]()
lub innymi słowy
![]()
. (7)
6. Błąd przeciętny jest to średnia arytmetyczna bezwzględnych wartości błędów prawdziwych
![]()
, (8)
gdzie n jest liczbą błędów prawdziwych.
Doświadczalnie ustalono następującą zależność błędu przeciętnego od błędu średniego:
![]()
i wzajemnie
![]()
Błąd przeciętny rzadko jest stosowany w praktyce. Ma on zastosowanie w pracach naukowych przy dużej liczbie materiałów doświadczalnych.
7. Błąd prawdopodobny r jest to błąd leżący w środku szeregu błędów, ułożonego w kolejności ich bezwzględnej wartości, tj. mający w tym szeregu tę samą liczbę błędów mniejszych jak i większych od siebie. Zatem
![]()
,
jeżeli n jest parzyste;
![]()
jeżeli n jest nieparzyste.
Wagi spostrzeżeń
Pomiary określonej wielkości wykonywane w różnych warunkach, różnymi przyrządami, przez różnych obserwatorów nazywamy spostrzeżeniami niejednakowo dokładnymi. Porównanie niejednakowo dokładnych obserwacji można przeprowadzić za pomocą ich średnich błędów lub za pomocą charakterystyk względnych, tj. wag spostrzeżeń. Jeżeli średnie błędy dwóch spostrzeżeń są jednakowe, to obserwacje te są jednakowo dokładne, a wagi ich są sobie równe. Jeżeli przy pomiarach jednego dnia dla określenia dowolnej wielkości ze średnim błędem ± rn należało wykonać obserwacje jeden raz, a innego dnia dla osiągnięcia tej samej dokładności należało powtórzyć obserwacje czterokrotnie, to pojedyncza obserwacja wykonana pierwszego dnia ma wagę czterokrotnie większą od pojedynczej obserwacji wykonanej drugiego dnia.
Przy pomiarach długości przyjmuje się wagi odwrotnie proporcjonalne do długości boku. Przy pomiarach niwelacyjnych przyjmuje się wagi odwrotnie proporcjonalne:
a) do długości ciągu, jeżeli zachowuje się stałą odległość między niwelatorem a łatami,
b) do liczby stanowisk niwelatora, gdy długości celowych są zmienne.
Przy pomiarach kąta w seriach liczba serii jest wagą. Przy pomiarze kątów w poligonach o bardzo różnych długościach boków wagą może być suma długości obu jego ramion itp.
Wagi spostrzeżeń są to liczby odwrotnie proporcjonalne do kwadratów błędów średnich tych spostrzeżeń:
![]()
(9)
Jeżeli znane są średnie błędy spostrzeżeń, to możemy wagę jednego z nich przyjąć za równą jedności, a pozostałe wagi obliczyć z wzoru
![]()
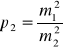
. (10)
Spostrzeżenie, dla którego przyjęto wagę p = 1, nazywane jest spostrzeżeniem jednostkowym albo typowym. Średni błąd spostrzeżenia jednostkowego oznaczamy przez ![]()
. Ogólny wzór na wagę i-tej obserwacji przyjmuje zatem postać
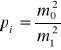
. (11)
Jeżeli średnie błędy obserwacji nie są znane, to za spostrzeżenia jednostkowe (o wadze p = 1) przyjmuje się wielkość umowną, np. pomiar kąta w jednej serii, pomiar na jednym stanowisku niwelacyjnym, pomiar długości 100-metrowego odcinka itp., a następnie według przyjętych zasad oblicza się wagi wielkości obserwowanych. W tym wypadku wartość średniego błędu spostrzeżenia przyjętego za jednostkowy otrzymuje się z wyrównania.
Prawo przenoszenia się błędów
Prawo przenoszenia się błędów w przypadku ogólnym określamy z wzoru
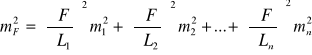
(12)
Wzór ten pozwala na obliczenie błędu średniego ![]()
funkcji
![]()
niezależnych n spostrzeżeń ![]()
o znanych błędach średnich ![]()
. Jeżeli błędy średnie wszystkich spostrzeżeń są sobie równe, tj. jeżeli ![]()
, to wówczas
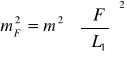
(13)
Na podstawie wzoru (9) prawo przenoszenia się wag określamy z wzoru ogólnego
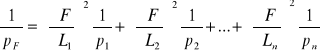
(14)
Wzory ogólne (12) i (14) mogą w przypadkach szczególnych przyjmować postaci następujące:
Jeżeli funkcja ma kształt sumy lub różnicy
![]()
;
a) dla spostrzeżeń niejednakowo dokładnych
![]()
; (15)
![]()
; (16)
b) dla spostrzeżeń jednakowo dokładnych
![]()
, (17)
![]()
; (18)
a gdy ![]()
![]()
; (18a)
gdzie n jest liczbą spostrzeżeń.
2. Jeżeli funkcja ma kształt iloczynu wartości stałej przez spostrzeżenie
![]()
;
wówczas
![]()
(19)
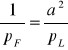
; (20)
3. Dla funkcji liniowej
![]()
otrzymamy:
![]()
(21)
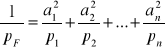
(22)
Zadania
Zadanie 1. Pewną wielkości zmierzono dziesięciokrotnie metodami I i II. Znając prawdziwą wartość tej wielkości otrzymano, zamieszczone w tabeli, błędy prawdziwe![]()
. Obliczyć błędy przeciętne i średnie wartości otrzymanych metodami I i II.
Metoda I |
Metoda II |
||||
n |
ε |
εε |
n |
ε |
εε |
1 |
+ 2 |
4 |
1 |
+ 1 |
1 |
2 |
-5 |
25 |
2 |
0 |
0 |
3 |
-4 |
16 |
3 |
-10 |
100 |
4 |
+ 8 |
64 |
4 |
+ 2 |
4 |
5 |
-6 |
36 |
5 |
0 |
0 |
6 |
-8 |
64 |
6 |
-8 |
64 |
7 |
-3 |
9 |
7 |
+ 15 |
225 |
8 |
+ 4 |
16 |
8 |
-4 |
16 |
9 |
+ 1 |
1 |
9 |
+ 3 |
9 |
10 |
-2 |
4 |
10 |
0 |
0 |
[ε] |
43 |
|
|
43 |
|
[εε] = 239 |
[εε] = 419 |
||||
Rozwiązanie. Błąd przeciętny jest dla obu metod jednakowy i wynosi
![]()
.
Błąd średni metody I:
![]()
Błąd średni metody II:
![]()
Metodą I uzyskano wyniki bardziej zbliżone do wartości prawdziwych iloczynów, a zatem dokładniejsze, podczas gdy wyniki metody II są bardziej rozstrzelone, a wiec mniej dokładne. Widzimy z powyższego przykładu, że błąd średni lepiej charakteryzuje dokładność metody niż błąd przeciętny, który w obu przypadkach jest jednakowy.
Jeżeli zgodnie z wzorem przybliżonym obliczymy błąd przeciętny na podstawie błędu średniego, to otrzymamy:
![]()
;
![]()
;
co zbliżone jest do uprzednio obliczonej wartości t = 4,3.
Zadanie 2. Sumy kątów w trójkątach siatki triangulacyjnej mają odchyłki od teoretycznej wartości 200g podane w tablicy 2. Obliczyć błąd średni i błąd przeciętny sumy kątów w trójkącie oraz określić dokładność wyznaczenia pojedynczego kąta.
Nr trójkąta |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Odchyłka εcc |
+ 20 |
-42 |
+ 90 |
+ 6 |
-88 |
+ 32 |
-12 |
-52 |
+ 8 |
-68 |
Różnicę między wartością teoretyczną sumy kątów a sumą otrzymaną na podstawie pomiarów można traktować jako błędy prawdziwe sumy kątów. Błąd średni sumy kątów w trójkącie wyniesie więc
![]()
Błąd przeciętny sumy kątów w trójkącie:
![]()
;
![]()
.
Dokładność wyznaczenia pojedynczego kąta w sieci według wzoru Ferrero
![]()
.
Obliczanie tych błędów ma zastosowanie przy badaniu, czy dawna sieć triangulacyjna odpowiada wymaganiom instrukcji dzisiejszych.
Zadanie 3. Zbadać, czy istniejąca siatka triangulacji miejskiej odpowiada wymaganiom instrukcji B-II. Jest to sześciobok z punktem centralnym. Na podstawie pomierzonych kątów w trójkątach obliczono odchyłki zamknięcia podane w tablicy 3. Natomiast kąty w siatce uzyskały poprawki wyrównawcze (błędy pozorne) podane w tablicy 4.
Nr trójkąta |
1 |
2 |
3 |
4 |
5 |
6 |
Odchyłka εcc |
+ 15 |
+ 15 |
-30 |
+ 45 |
+ 15 |
-15 |
Nr kąta |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Popr. vcc |
+ 5,2 |
+ 4,9 |
+ 5,2 |
+ 4,9 |
-10,2 |
-10,5 |
+ 15,4 |
+ 15,4 |
+ 5,2 |
Nr kąta |
10 |
1l |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
Popr. vcc |
+ 4,9 |
-4,9 |
-5,2 |
+ 5,2 |
+ 5,2 |
-10,2 |
+ 15,4 |
+ 5,2 |
-5,2 |
Średni błąd kąta wyrównanego obliczymy z wzoru przybliżonego
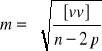
;
gdzie v — poprawka wyrównawcza kąta spostrzeganego,
n = 18 — liczba kątów,
p = 6 — liczba określanych punktów (1 punkt jest znany),
![]()
Wzór Ferrero daje wynik niewiele odbiegający od wyniku obliczonego wg powyższego wzoru przybliżonego:
![]()
Badana siatka odpowiada zatem wymaganiom instrukcji B-II.
Wzór Ferrero zwykle daje ocenę zbliżoną do oceny dokładności wyznaczenia kąta w sieci, otrzymanej na podstawie wyrównania tej sieci.
Zadanie 4. Zbadać dokładność liniową siatki triangulacyjnej na podstawie względnych błędów boków. W łańcuchu złożonym z 6 trójkątów dany jest błąd względny boku wyjściowego W0 = 1 : 58 600 oraz średni błąd kąta ![]()
.
Rozwiązanie. Stosujemy wzór przybliżony
![]()
,
gdzie ![]()
— błąd względny badanego boku,
n — liczba trójkątów od boku wyjściowego do boku badanego. Po wstawieniu wartości szczegółowych otrzymujemy
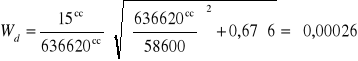
;
![]()
.
Jest to siatka zbyt mało dokładna wobec wymagania instrukcji B-II, aby względny błąd pomiaru bazy w siatce triangulacyjnej IV rzędu wynosił 1 : 50 000, czyli 0,002%.
Zadanie 5. Średni błąd kąta pomierzonego w dwóch seriach (s = 2) wynosi m = ±4". W ilu seriach s należy wykonać pomiar kąta w tych samych warunkach, przez tego samego obserwatora i tym samym instrumentem, aby otrzymać dwa razy większą dokładność, tj. dwa razy mniejszy średni błąd kąta.
Rozwiązanie. Przyjmujemy wagę kąta mierzonego w jednej serii p = 1, a więc waga kąta mierzonego w dwóch seriach wyniesie p = 2,
![]()
;
![]()
;
![]()
;
![]()
.
Ponieważ wielkość wagi odpowiada w tym przypadku liczbie serii koniecznych do osiągnięcia żądanej dokładności, więc liczba serii wyniesie s = 8. Aby otrzymać dwa razy większą dokładność, należy wykonać pomiar w 4 razy większej liczbie spostrzeżeń.
Zadanie 6. Tematem polowych ćwiczeń szkolnych była niwelacja techniczna, wykonana na trasie niwelacji państwowej, gdzie 11 reperów o znanych wysokościach n.p.m. miało równe odległości między sobą, wynoszące po 2 km. Przyjmując spady między reperami państwowymi za bezbłędne, obliczono odchyłki e między nimi a spadami ćwiczebnymi, podane w tablicy 5. Obliczyć błąd przeciętny, prawdopodobny i średni niwelacji ćwiczebnej.
Nr spadu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Odchyłka ε mm |
+ 5 |
-4 |
+ 2 |
-2 |
+4 |
-7 |
+ 3 |
-5 |
+ 3 |
+ 6 |
Rozwiązanie.
![]()
;
![]()
;
![]()
.
Zadanie 7. Kąt a pomierzono niezależnie od siebie dwa razy: 1) w 2 seriach, 2) w 50 seriach, otrzymując w obu wypadkach tę samą wartość na średni błąd pojedynczego spostrzeżenia m = ±1". Obliczyć wartość w m, czyli błąd średni błędu średniego.
Rozwiązanie:
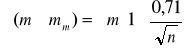
;
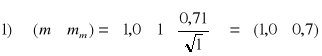
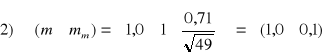
Z powyższego zadania wynika, że do oceny dokładności można mieć w drugim wypadku dużo większe zaufanie niż w wypadku pierwszym. Prawdopodobieństwo, że średni błąd spostrzeżenia w prawidłowy sposób określa rzeczywistą dokładność wyznaczenia, jest tym większe, im większą jest liczba spostrzeżeń nadliczbowych. Stopień zaufania do oceny dokładności określa wielkość mm.
Zadanie 8. W trójkącie pomierzono dwa kąty z błędami średnimi
![]()
;
![]()
.
Obliczyć trzeci kąt y i jego błąd średni. Rozwiązanie:
![]()
;
![]()
stosujemy zatem wzór (17) i otrzymujemy:
![]()
;
![]()
Z wzoru (18), przyjmując wagę kąta zmierzonego ![]()
, obliczymy:
![]()
.
Jeżeli funkcja zależy od dwóch mierzonych zmiennych, co właśnie zachodzi w tym zadaniu, to jej błąd obliczamy z wzoru (12). Podobieństwo tego wzoru do twierdzenia Pitagorasa pozwala na jego przedstawienie graficzne (rys. 1). Stosując ten rysunek do szczególnych wartości niniejszego zadania, otrzymujemy rysunek
(rys. 2) pozwalający graficznie ustalić wielkość średniego błędu trzeciego kąta w trójkącie.
Wniosek. Jeżeli w terenie nie ma przeszkód uniemożliwiających pomiar wszystkich kątów w trójkącie lub — ogólnie mówiąc — w poligonie, to należy mierzyć wszystkie kąty, gdyż — jak widzimy z powyższego zadania — kąt obliczany jest znacznie mniej dokładny niż kąty mierzone.
Zadanie 9. W 10-bocznym zamkniętym poligonie pomierzono 9 kątów z błędem średnim każdego kąta ![]()
. Jaki będzie błąd średni obliczonego kąta dziesiątego?
Rozwiązanie:
![]()
.
Stosujemy wzór (17)
![]()
;
![]()
Jeżeli przyjmiemy wagę kąta zmierzonego ze średnim błędem ![]()
za równą p = 1, to na podstawie wzoru (18) będzie
![]()
; ![]()
.
Widzimy tu bardzo znaczną różnicę w dokładności kątów mierzonych i kąta obliczonego.
Zadanie 10. Otwarty ciąg poligonowy ma 14 kątów; jaki będzie średni błąd azymutu końcowego, jeżeli błąd azymutu początkowego ![]()
, a błąd każdego kąta ![]()
?
Rozwiązanie:
![]()
.
Stosujemy wzór (21):
![]()
;
![]()
.
Jeżeli przyjmiemy wagę p = 1 dla kąta zmierzonego ze średnim błędem ![]()
. to stosując wzór (11) otrzymujemy
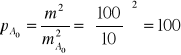
;
a następnie wg wzoru (22):
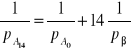
;
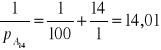
;
![]()
.
Sprawdzenie:
![]()
;
![]()
;
![]()
.
Zadanie 11. Pomiar różnicy wysokości między dwoma reperami ze względu na odległość między nimi wymaga 20 stanowisk niwelatora, ustawianego w środku między łatami. Błąd odczytu każdej łaty m = ±1 mm. Jaki będzie błąd różnicy wysokości między tymi reperami?
Rozwiązanie. Różnica wysokości na jednym stanowisku
![]()
.
Takich różnic będzie 20, a odczytów na łacie 40, stosując więc do obliczenia średniego błędu różnicy wysokości między reperami wzór (17) otrzymamy:
![]()
![]()
Jeżeli waga każdego odczytu na łacie ![]()
, to waga każdego spadu ![]()
, a waga różnicy wysokości między reperami, obliczona wg wzoru (18a), wyniesie:
![]()
;
![]()
.
Zadanie 12. Dalmierzem kreskowym o stałych k = 100 i c = 0 zmierzono odległość d. Długość odczytanego odcinka na łacie l = 100 cm, błąd odczytu każdej kreski dalmierczej m = ±1 mm. Jaki będzie błąd odległości?
![]()
;
![]()
;
![]()
.
Zadanie 13. Na mapie zmierzono odległość między dwoma punktami, przy czym błąd przyłożenia zera podziałki mp = ±0,1 mm, a błąd odczytu m0 = ±0,15 mm. Jakiego błędu należy oczekiwać przy zmierzonej długości? Rozwiązanie. Stosujemy wzory (15) i (16):
![]()
;
jeżeli wagę odczytu przyjmiemy ![]()
, wówczas
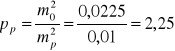
;
![]()
.
![]()
.
Zadanie 14. W prostokącie zmierzono boki
![]()
;
![]()
.
Obliczyć pole prostokąta i jego błąd średni. Rozwiązanie:
![]()
.
Do obliczenia błędu średniego stosujemy wzór (12):
![]()
.
Po wstawieniu wartości szczegółowych otrzymujemy
![]()
czyli
![]()
Zadanie 15. Aby obliczyć powierzchnię budynku, zmierzono jego boki i stwierdzono, że jest to kwadrat o boku a = 29,15±0,02 m. Obliczyć pole tego kwadratu i jego błąd średni.
Rozwiązanie:
![]()
.
Stosujemy wzór (12)
![]()
; ![]()
.
a, więc
![]()
.
Zadanie 16. W trójkącie pomierzono podstawę a = 29,70±0,02 m i wysokość w = 10,16±0,01 m. Obliczyć pole trójkąta i jego błąd średni.
Rozwiązanie:
![]()
.
Stosujemy wzór (12):
![]()
![]()
![]()
.
Zadanie 17. Zmierzono promień koła R = 25,75±0,02 m. Obliczyć obwód i pole koła oraz ich błędy średnie.
Rozwiązanie:
![]()
![]()
;
![]()
![]()
![]()
![]()
Zadanie 18. W trapezie pomierzono dwa boki równoległe i wysokość, otrzymując następujące wyniki:
![]()
;
![]()
;
![]()
.
Obliczyć pole trapezu, jego błąd średni i błąd względny.
Rozwiązanie:
![]()
;
![]()
![]()
![]()
.
Błąd względny wynosi:
![]()
.
Rachunek kontrolny błędu średniego jest tu możliwy według wzoru (23), o ile obliczymy najpierw średni błąd sumy boków równoległych, który wynosi
![]()
;
a następnie tę sumę będziemy uważać jako jedną zmienną.
Zadanie 19. Planimetrem biegunowym o stałej
![]()
pomierzono powierzchnię działki i otrzymano różnicę odczytów kółka całkującego
![]()
.
Obliczyć powierzchnię działki, jej błąd średni i błąd względny.
Rozwiązanie:
![]()
;
![]()
![]()
![]()
;
![]()
.
Zadanie 20. Planimetrem biegunowym o stałych
![]()
![]()
pomierzono powierzchnię działki przy biegunie wewnątrz działki i otrzymano różnicę odczytów kółka całkującego
![]()
.
Obliczyć powierzchnię działki, jej błąd średni i błąd względny.
Rozwiązanie:
![]()
![]()
![]()
![]()
![]()
.
Rachunku kontrolnego za pomocą poprawek logarytmicznych stosować tu nie można.
Zadanie 21. W trójkącie pomierzono bok i dwa kąty do niego przyległe:
![]()
;
![]()
;
![]()
.
Obliczyć trzeci kąt ![]()
, boki b i c, ich błędy średnie oraz błędy względne boków.
Rozwiązanie: Do obliczenia średniego błędu trzeciego kąta a stosujemy wzór (15):
![]()
.
Bok b obliczamy wg wzoru
![]()
;
a do obliczenia jego błędu średniego stosujemy wzór (12) i w tym celu obliczamy pochodne cząstkowe:
![]()
;
![]()
;
![]()
.
Boki b i c obliczamy w tabeli.
Kąty |
Grady |
sin |
Boki |
ctg |
ctg2 |
|
α β γ |
64,56 73 70,14 75 65,28 52 |
0,849 068 0,892 052 0,854 972 |
a b c |
150,15 157,75 151,19 |
0,622 189 0,506 610 0,606 656 |
0,38 712 0,25 665 0,36 803 |
|
200,00 00 |
|
|
|
||
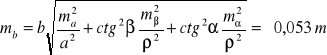
.
Przeprowadzając analogiczny rachunek za pomocą pochodnych cząstkowych oraz rachunek kontrolny za pomocą poprawek logarytmicznych, otrzymamy
![]()
.
Błędy względne:
![]()
![]()
Uwaga. We wzorach na błędy średnie funkcji przy użyciu jej pochodnych cząstkowych należało zamienić miarę kątową, w jakiej podane są błędy średnie kątów, na miarę łukową, dzieląc je przez radian ρcc = 636 620".
Zadanie 22. W trójkącie pomierzono dwa boki i kąt leżący naprzeciwko boku większego
![]()
;
![]()
;
![]()
.
Obliczyć kąt ![]()
i jego błąd średni.
Rozwiązanie:
Wzór sinusowy
![]()
zamieniamy, na
![]()
Stosujemy teraz wzór (12)
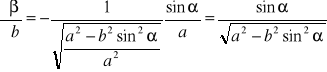
;
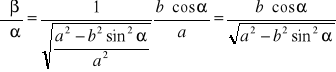
;
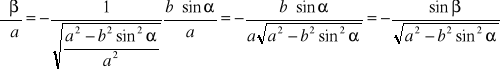

![]()
.
Zadanie 23. W trójkącie pomierzono dwa boki i kąt leżący naprzeciw większego z nich:
![]()
;
![]()
;
![]()
.
Obliczyć kąt ![]()
i jego błąd średni.
Odpowiedź:
![]()
Zadanie 24. W trójkącie pomierzono dwa boki i kąt leżący naprzeciw większego z nich:
![]()
Wilhelm Chojnicki - Geodezyjny rachunek wyrównania w zadaniach
7
A
B
C
![]()
![]()
![]()
∙
![]()
∙
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Obliczenia Błędy średnie, Geodezja i Kartografia, Rachunek Wyrównawczy
Z Obliczenia dla sieci kątowej, Geodezja i Kartografia, Rachunek Wyrównawczy
Sieci płaskie, Geodezja i Kartografia, Rachunek Wyrównawczy
Obliczenia na liczbach przybliżonych, Geodezja i Kartografia, Rachunek Wyrównawczy
Ćw. 1 Zastosowanie form rachunkowych Hausbrandta, Geodezja i Kartografia, Rachunek Wyrównawczy
S 7 Równania obserwacji 3, Geodezja i Kartografia, Rachunek Wyrównawczy
Wyrównanie parametryczne - metoda macierzowa, Geodezja i Kartografia, Rachunek Wyrównawczy
Wagi i błędności, Geodezja i Kartografia, Rachunek Wyrównawczy
Wyrównania korelat, Geodezja i Kartografia, Rachunek Wyrównawczy
Ściaga RW, Geodezja i Kartografia, Rachunek Wyrównawczy
Z Wyrównanie obserwacji bezpośrednich, Geodezja i Kartografia, Rachunek Wyrównawczy
Równania ogólne poprawek, Geodezja i Kartografia, Rachunek Wyrównawczy
S 6 Spostrzeżenia niejednakowo dokładne, Geodezja i Kartografia, Rachunek Wyrównawczy
S 6 Spostrzeżenia bezpośrednie, Geodezja i Kartografia, Rachunek Wyrównawczy
Miary dokładności spostrzeżeń, Geodezja i Kartografia, Rachunek Wyrównawczy
Sieci wysokościowe regionalne, Geodezja i Kartografia, Rachunek Wyrównawczy
Podstawowe zasady wyrównania, Geodezja i Kartografia, Rachunek Wyrównawczy
więcej podobnych podstron