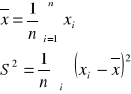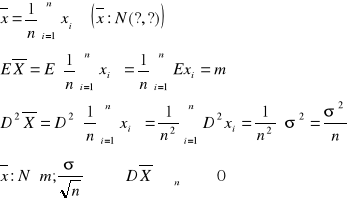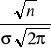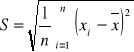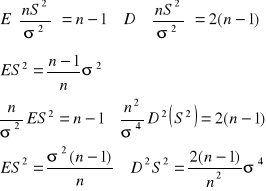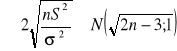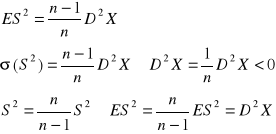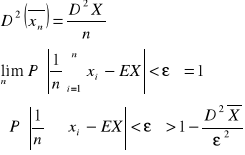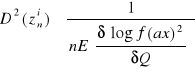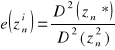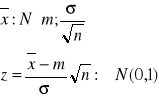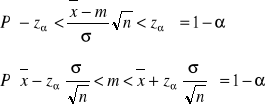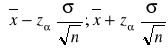WNIOSKOWANIE STATYSTYCZNE: Jest to uogólnienie wyników otrzymanych w próbie na populacje generalną. ESTYMACJA - próba losowa prosta x - zmienna losowa określona w populacji generalnej DEFINICJA 1: (x1, x2, ..., xn) xi - zmienne niezależne, mają ten sam rozkład co zmienna losowa x (x1, x2, ..., xn)→ (x1, x2, ..., xn) - realizuje próby losowej prostej DEFINICJA 2: przestrzeń prób KI={(x1, x2, ..., xn)} i = 1, 2, ..., n DEFINICJA 3: Statystyką nazywamy funkcje określoną na próbie losowej prostej. U = f(x1, x2, ..., xn) U - statystyka z próby np. (x1, x2, ..., xn) U = f(x1, x2, ..., xn) = xi UWAGA: Rozkład statystyk z próby zależy od: rozkładu zmiennej losowej liczebności z próby PRZYKŁADY WYBRANYCH STATYSTYK: Rozkład średniej arytmetycznej z próby: a). x: N(m,σ) (x1, x2, ..., xn) - próba losowa prosta m x statystyka b). σ - nieznane statystyka ma rozkład studenta o (n-1) stopniach swobody S - odchylenie standardowe z próby losowej prostej (n →α) ⇒ Tn-1 ≈ N(0,1) Rozkład wariancji z próby: x: N(m,σ) statystyka ma rozkład UWAGA: WNIOSEK: n > 30 ESTYMACJA - szacowanie parametrów lub rozkłądów populacji generalnej na podstawie wyników zaobserwowanych w próbie estymacja parametryczna (określenie parametrów rozkładu) estymacja nieparametryczna (typ funkcji gestości lub funkcji rozkłądu prawdopod. określ.) ESTYMACJA PARAMETRYCZNA: estymacja punktowa polega na oszacowaniu parametru podając jego wartość estymacja przedziałowa podaje przedział, w którym ten parametr się znajduje Estymatorem parametru Q nazywamy statystykę zn = f(x1, x2, ..., xn), której rozkład zależy od szacowanego parametru. Estymator jest zmienną losową. Rozkład zn zalezy od szacowanego parametru. zn = f(x1, x2, ..., xn) - ocena parametru Q Wartość estymatora dla dowolnego elementu przestrzeni prób jest to ocena param. Q. d = zn - Q - błąd estymatora Δ = E(zn - Q)^2 - miara błędu estymatora UWAGA: Ezn = 0 ⇒ Δ = D^2zn Dzn - średni błąd szacunku param. Q WŁASNOŚCI ESTYMATORÓW: nieobciążność zgodność efektywność dostateczność Estymator param. Q jest nieobciążony jeśli Ezn = Q Ezn - Q = σ (2n) σ (2n) - obciążoność estymatora PRZYKŁAD 1: x - zmienna losowa o nieznanym rozkładzie (x1, x2, ..., xn) - próba losowa prosta Q = EX zn : zn = xi EXi = EX PRZYKŁAD 2: (wariancja estymatora) D^2X = Q S^2 = DEFINICJA 1: - estymator asymptotycznie nieobciążony DEFINICJA 2: Estymator param. Q jest zgodny jeśli: ; ε - dowolne UWAGA: Jeżeli zn jest estymatorem zgodnym to jest estymatorem nieobciążonym. Jeżeli zn jest nieobciążony i to zn jest estymatorem zgodnym EFEKTYWNOŚĆ: Niech {zn^1, zn^2, ..., zn^k}; Ezn^i = Q l = 1, ..., k DEFINICJA 1: Estymator zn* spełniający warunek: min{D^2(zn^l)} = D^2(zn*) ; 1 ≤ i k zn* - najefektywniejszy estymator param. Q NIERÓWNOŚĆ RAO - GAMERA: f - funkcja gęstości zm. los. x efektywność zn^i e (.) ∈ (0,1> zn asymptotycznie najefektywniejszy DEFINICJA 2: Zn - dostateczna, jeżeli zawiera wszystkie informacje dotyczące parametru Q wystepującego w próbie losowej prostej ESTYMACJA PRZEDZIAŁOWA: DEFINICJA 1: Przedziałem ufności param.Q nazywamy przedział spełniający nastepujący warunek: P{g1(zn) < Q < g2(zn)} = 1- α [g1(zn) ; g2(zn)] - przedział ufności 1 - α - współczynnik ufności (1 - α = 0,90 ∨ 0,95 ∨ 0,99) Przedział ufności dla średniej w populacji normalnej. A: x: N(m,σ) m=? σ - znane (x1, x2, ..., xn) - próba losowa prosta 1 - α - zadany Zn: P{-zα < z < zα} = 1 - α f(x) 1 - α - zα zα z ( ) - przedział ufności dla EX UWAGA: (x1, x2, ..., xn) ∈ kl ⇒ - liczbowy przedział ufności f(x) xn xn xn xn xn m x WZGLĄDNA PRECYZJA SZACUNKU: 5%< ≤ 10% - uogólnianie wyników z próby na populacje; dobrac ostroznie > 10% - nie przeprowadzać uogólnień

---