Na dzisiejszych zajęciach omówimy Maszynę Turinga. Maszyna Turinga to stworzony przez Alana Turinga abstrakcyjny model komputera służący do wykonywania algorytmów. Składa się ona z bloku sterowania, głowicy odczytująco - zapisującej i nieskończenie długiej taśmy z jednobitowymi komórkami. Maszyna Turinga, a konkretnie jej działanie możemy zapisać w formie grafu i ogolnie mówimy, że maszyna ta to jest taka uporządkowana szóstka: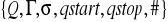
. Q to skończony zbiór stanów maszyny zawierający wyróżniony stan początkowy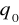
i dwa stany kocowe:
dla odpowiedzi tak, oraz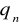
dla odpowiedzi nie.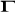
to zbiór skończony symboli taśmy.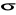
z kolei to funkcja przejścia, qstart to stan początkowy, a qstart - stan końcowy. Symbol # zwany haszem oznaczający puste miejsce na taśmie maszyny. Funkcję przejść oznaczoną jako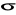
możemy zapisać w nastepujący sposób: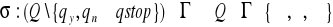
. Te strzałki wskazują kierunek poruszania się głowicy. Strzałka skierowana w dół oznacza, że głowica nie zmienia położenia. Na dzisiejszych ćwiczeniach będziemy mówić o maszynie, która posiada jedną taśmę i jedną głowicę mimo, iż w rzeczywistości mówi się o maszynach wielotaśmowych i wielogłowicowych. Maszynę Turinga możemy podzielić na deterministyczną i niedeterministyczną. Nim jednak powiemy co to znaczy warto powiedzieć kilka słów o automacie skończonym. Jest to taki automat, który służy tylko i wyłącznie do rozpoznania jakiegoś wzorca zapisanego na taśmie. I nie jest on w stanie wykonać powrotu w lewo (zawsze idzie w prawą stronę) i nie może zmieniać zawartości taśmy.Przejdźmy teraz do maszyny deterministycznej. Załóżmy, że mamy taśmę obustronnie nieskończoną z nieskończoną liczbą klatek, na której zapisany jest dowolny ciąg liter (alfabetem taśmowym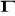
będzie w naszym przypadku zbiór symboli od a do z) tak, jak na poniższym rysunku:

…

c

a

x

y

z

b

d

…

Głowica ustawiona jest przy literze c. I na przykład interesuje nas zbudowanie takiej maszyny Turninga, która będzie sprawdzała, czy analizowany ciąg zawierał będzie zbiór symboli xyz jeden po drugim (rozpoznanie wzorca xyz na taśmie). Taką maszynę można narysować za pomocą następującego grafu:

Wierzchołki tego grafu oznaczają stan, w jakim znajduje się maszyna Turinga, natomiast w gałęziach zawarte są funkcje przejścia. Stan początkowy maszyny został oznaczony strzałką z oznaczeniem na górze: start. I widzimy wyraźnie działanie tej maszyny. Najpierw maszyna przesuwa się po taśmie szukając pierwszej litery - x. Jeśli jej nie znajdzie przesuwa się na następną klatkę (zostaje w stanie 0) i znów jej wyszukuje. Natomiast jeśli ją znajdzie (przechodzi w stan 1), to sprawdza, czy następna klatka zawiera literę y. Jeśli nie, przesuwa się znów na następną klatkę i szuka od nowa litery x (znów przechodzi w stan 0), potem y i z. Jeśli znajdzie na pierwszej klatce literę x (stan 1), na drugiej - y (stan 2), a na trzeciej z (stan 3), to maszyna kończy swoją pracę. Zasada działania jest więc dosyć prosta. Przejdźmy teraz do maszyny niedeterministycznej i zobaczymy, czym te dwie maszyny się różnią. Najpierw deterministyczna - jesteśmy w jakimś stanie Q, czytamy znak q i mamy tylko jedno polecenie które nam mówi co teraz możemy zrobić. Z kolei w niedeterministycznej jesteśmy w jakimś stanie Q, czytamy znak q i teraz się okazuje że mamy kilka poleceń które do obecnego stanu pasują. Zobaczmy, jak wygląda ten sam problem rozpatrywany przez nas na grafie maszyny niedeterministycznej:

Jak widać ta maszyna ma znacznie więcej możliwości. No i teraz poróbmy kilka zadań. Najpierw zadanie pierwsze. Mamy daną nastepującą taśmę:

…

#

0

1

0

1

1

#

…

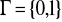
. Należy narysować w postaci grafu maszynę Turinga (dowolną), która zbada parzystą liczbę jedynek w danym ciągu nieskończonym. A. Oczywiście zakładamy, że głowica ustawiona będzie w komórce z zawartością #. Graf będzie miał postać następującą:

Kolejne zadanie polegać będzie na programowej implementacji tej maszyny rozwiązującej powyższy problem. A oto pseudokod:

int stan=0;

int i=0;

while (tab[i]!=”#”)

{

if (tab[i]==1){

stan=1-stan;

}

i++;

}

I nastepne zadanie. Należy narysować graficznie maszynę Turinga, która sprawdza, czy w ciągu zerojedynkowym zapisanym na taśmie tak, jak wyżej występuje ciąg zawierający więcej niż dwie jedynki pod rząd. Jeśli wystepuje, maszyna ma zwrócić odpowiedź: tak. A zatem graf dla tego problemu wygląda następująco:

I następne zadanie. Należy graficznie narysować taka maszyne Turinga, która w ciągu zerojedynkowym zapisanym na taśmie sprawdzi, czy zera i jedynki w tym ciągu występują naprzemiennie. Rozwiązanie ma się odnosić do ciągu zerojedynkowego rozpoczynającego się od 0, jak również ciągu rozpoczynającego się od 1. Wówczas graf rozwiązujący ten problem będzie wyglądał nastepująco:

A teraz załóżmy, że mamy zaimplementowany jakiś program. Należy narysować taką maszynę Turinga, która sprawdzi, czy w kodzie pojawiają się komentarze autora. Znak początku komentarza to /*, a znak końca, to */. A zatem graf będize wyglądał tak:

I nastepny problem. Tym razem nie będizemy rozpatrywali maszyn odczytujących, ale rozpatrzymy maszyne modyfikującą i zadaniem tej maszyny ma być operowanie na ciągu zerojedynkowym w taki sposób, by zamienić w nim ciąg 11 na a, oraz ciąg 000 na literkę b w tym ciągu. Oto graf wykonujący tę operację:

I nastepne zadanie. Należy napisać taką maszynę, która posegreguje cią zerojedynkowy i ustawi jedynki na lewo, a zera na prawo. I tak:

I ostatnie z zadań. Mamy dany ciąg zerojedynkowy: #01011#. Należy stworzyć taką maszynę Turinga, która sprawdzi, jaki jest środkowy element ciągu (jeśli nie ma, to koniec programu) i dopisze go na koniec ciągu (W tym wypadku jest to 0). A zatem graf wygląda tak:

---