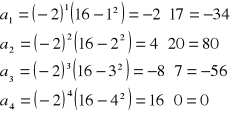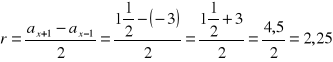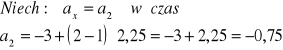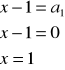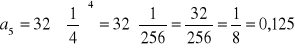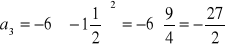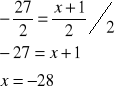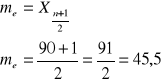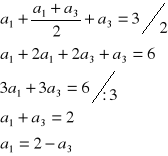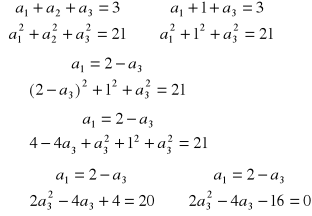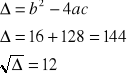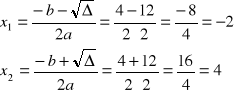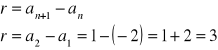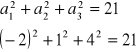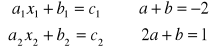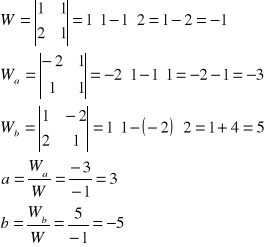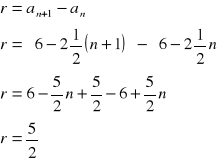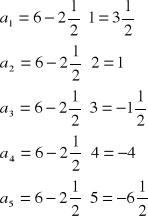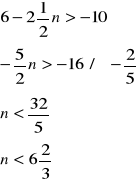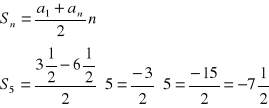ZADANIA ZAMKNIĘTE:
1.	Mamy ciąg:
		Podstawiamy za n po kolei lub od razu a4.
	Odp. C
2.	Mamy trzy kolejne wyrazy ciągu:
		Obliczamy różnicę (r) między wyrazami ciągu
		Wzór na n-ty wyraz ciągu arytmetycznego
		Przyjmujemy ax = a2 i podstawiamy
	Odp. A
3.	Mamy
		Obliczamy różnicę (r)
		podstawiamy
		Obliczamy a1
		Podstawiamy i obliczamy x
	Odp. B
4.	Mamy kolejne wyrazy ciągu geometrycznego: 32, 8, 2, , x
	Przyjmijmy: an = 8 i an+1 = 2
		Obliczamy iloraz ciągu (q)
	Niech: to
		Wtórna na n-ty wyraz ciągu geometrycznego
		Podstawiamy i obliczamy
	Odp. D

5.	Mamy trzy kolejne wyrazy ciągu geometrycznego:
	Niech
		Obliczamy iloraz ciągu (q)
		Wtórna na n-ty wyraz ciągu geometrycznego
		Podstawiamy i obliczamy x
	Odp. D
6.	Dane z próby: 1, 1, 1, 1, 3, 4, 4, 5, 5, 5, 6, 6, 7
	1 - 4 razy - to jest dominanta 3 - 1 raz 4 - 2 razy 5 - 3 razy 6 - 2 razy 7 - 1 raz	Dominantą z próby (modą lub wartością modalną) nazywamy taką wartość w próbie, która jest najliczniej reprezentowana.
	Odp. C
7.	Dane z próby: 2, 2, 4, 4, 5, 3, 3 n = 7
		Wzór na średnią arytmetyczną z próby ( )
	Odp. D

8.	Mamy dane z próby:
	l. książek	0		1		2		3		4		5
	l. osób	5		10		30		30		10		5
													Obliczamy ilość przeczytanych książek (ilość zdarzeń w próbie)
													Obliczamy ilość osób (ilość obserwacji w próbie)
													Wzór na średnią arytmetyczną z próby ( )
	45 uczniów przeczytało 2 książki i 45 uczniów przeczytało 3 książki, wiec me (wartość środkowa) Czyli me = 2,5												Mediana (wartość środkowa) wartość cechy w szeregu uporządkowanym, powyżej i poniżej której znajduje się jednakowa liczba obserwacji. Aby ją ustalić, dodajemy do liczby obserwacji 1 i sumę tę dzielimy przez 2.
	Odp. D
ZADANIA OTWARTE:
9.	Mamy dane z próby:
	l. filmów		1		2		3		4		5
	l. osób		4		8		6		1		5
													Obliczamy ilość obejrzanych filmów (ilość zdarzeń w próbie)
													Obliczamy ilość osób (ilość obserwacji w próbie)
													Wzór na średnią arytmetyczną z próby ( )
	4 + 8 = 12												Liczba osób, która przeczytała mniej książek niż średnią
	Odp. 50% ankietowanych przeczytało mniej niż średnią grupy.

10.	Mamy dany ciąg arytmetyczny taki, że:
	i
	rosnący więc
	Rozwiązanie:
					Wyraz a2 jest „po środku” między wyrazami a1 i a3
	więc
					Podstawiamy do sumy pierwszych trzech wyrazów ciągu (którą znamy) i obliczamy a1
					Obliczyliśmy a2
					Teraz tworzymy układ równań
	Niech: wówczas				Otrzymaliśmy równanie kwadratowe
					Obliczamy wyróżnik Δ , więc mamy dwa pierwiastki
					Obliczamy pierwiastki równania kwadratowego
	Ciąg rosnący więc
					Obliczamy różnicę (r)
	Sprawdzenie warunków:
	1) 2) Warunki spełnione.
	Wyznaczenie wzoru ogólnego:
	x	1	2	3	Ciąg liczbowy jest funkcją, więc wyznaczamy tabelkę.
		y	-2	1		4
					Na podstawie tabelki tworzymy układ równań
					Obliczamy układ równań metodą wyznacznikową.
	Z powyższego otrzymujemy:
	Z czego otrzymujemy ogólny wyraz ciągu:
11.	Dany jest ciąg:
	a) czy ciąg jest arytmetyczny?
					Ciąg jest arytmetyczny wtedy i tylko wtedy, gdy różnica (r) między dowolnym wyrazem ciągu, a wyrazem bezpośrednio go poprzedzającym jest stała dla danego ciągu.
	Odp. Ciąg an jest arytmetyczny.

	b) pięć początkowych wyrazów ciągu:
		Podstawiamy za n kolejno 1, 2, 3 itd. i obliczamy kolejne wyrazy ciągu.
	c) dla jakiego wartości n wyraz an > - 10
		Układamy nierówność z ogólnego wyrazu ciągu i warunku dla an i obliczamy n
	Odp. Dla
	d) suma pięciu początkowych wyrazów ciągu:
		Wzór na sumę n początkowych wyrazów ciągu Podstawiamy i obliczamy.
	Odp.
		UWAGA!
		Kolor zielony - komentarz

2

---