OGÓLNE WŁASNOŚCI FUNKCJI

Należy powtórzyć pojęcia:

• funkcja;

• dziedzina funkcji;

• zbiór wartości funkcji;

• miejsce zerowe funkcji;

• monotoniczność funkcji;

• różnowartościowość funkcji;

• parzystość i nieparzystość funkcji;

• okresowość funkcji;

• funkcja odwrotna.

1. W styczniu właściciel sklepu zanotował obroty wynoszące 10 450 zł, a w kolejnych miesiącach pierwszego półrocza obroty rosły o około 1000 zł miesięcznie. Narysuj wykres ilustrujący zyski w kolejnych miesiącach pierwszego półrocza, jeśli zysk stanowi około 20% obrotu. Podaj wzór i naszkicuj wykres tak określonej funkcji zysku od czasu.

2. Oblicz wartość podanych funkcji dla argumentów równych:
:

a)
b)
c)
d)

3. Wyznacz dziedzinę funkcji:

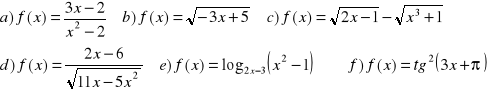
4. Wyznacz zbiór wartości podanych funkcji:

1. f(x) = -3x +2 dla x ∈ {-2/3, -1, 0, √5, 6} b)f(x) = ½ x² dla x ∈ {-√2, -
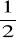
   , 0, √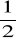
   , √2 /2}

c)f(x) =
dla x ∈ {1/2 ,5/8 , 1, 5, 13} d) f(x) = -3x+1 dla x ∈ R₊

e) f(x) = ˝ x dla x ∈ < -2, 2> f) f(x) = - x²+3 dla x ∈ R

5.Narysuj wykres funkcji
dla:

a)
b)
c)
d)
e)
f)

g)
h)

6. Które z punktów: (0,-2),(0,1), (0,-1/2), (0,2), (0,-1), (0,1/2), (0,0), (0,-2) należą do wykresów funkcji:

1. f(x)= - 3x+7 b)
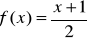
   c)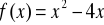
   d)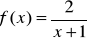
   

7. W oparciu o definicję funkcji różnowartościowej uzasadnij, że podane funkcje są różnowartościowe:

8.Uzasadnij, że podane funkcje nie są różnowartościowe: f(x) = -2x² ; f(x) = Ⴝ1-xႽ;

f(x)= ax² , gdzie a jest dowolną liczbą rzeczywistą

9.W oparciu o definicję uzasadnij, że podane funkcje w podanych zbiorach liczbowych są rosnące:

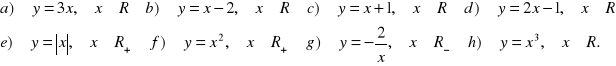
10. W oparciu o definicję uzasadnij, że podane funkcje w podanych zbiorach liczbowych są malejące:

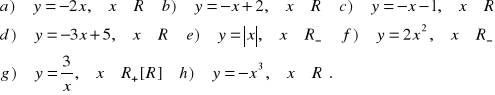
11.W oparciu o definicję zbadaj monotoniczność funkcji:

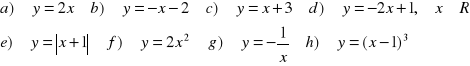
12. W oparciu o definicję funkcji parzystej uzasadnij, że podane funkcje są parzyste:

13.W oparciu o definicję funkcji nieparzystej uzasadnij, że podane funkcje są nieparzyste:

14.Zbadaj parzystość funkcji f(x)= x³sinx.

15. Wyznacz okres podstawowy funkcji f(x)=2cos(4x).

16. Narysuj wykresy podanych funkcji dla x ჎ <0, 9>:

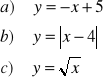
Podaj przedział na który funkcje te odwzorowują <0,9>.Naszkicuj wykresy funkcji odwrotnych do danych.

17. Wyznacz wzór funkcji odwrotnej do
.

2

---