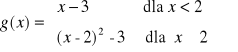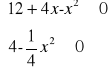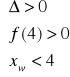FUNKCJA KWADRATOWA

Poziom podstawowy

Zadanie 1. (6 pkt.)

Liczbę 10 przedstaw w postaci sumy trzech liczb takich, że trzecia z nich jest o 4 większa od pierwszej tak, by suma ich kwadratów była najmniejsza.

Zadanie 2. (4 pkt.)

Współczynniki a, b, trójmianu kwadratowego
są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego o różnicy -5. Reszta z dzielenia trójmianu f przez dwumian
jest równa -4.

1. napisz równanie osi symetrii wykresu funkcji f

2. oblicz najmniejszą i największą wartość funkcji w przedziale
   .

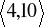
Zadanie 3. (3 pkt.)

Trójkąt prostokątny ma boki o długościach x, 2x-2, 2x-4. Oblicz pole tego trójkąta.

Zadanie 4. (5 pkt.)

Wyznacz wartości x, dla których z odcinków a,b,c można zbudować trójkąt, jeżeli
,
,
.

Zadanie 5. (3 pkt.)

Wykres funkcji g powstał z wykresu funkcji f określonej wzorem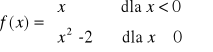

wskutek przesunięcia o 2 wzdłuż osi X oraz o -1 wzdłuż osi Y.

1. naszkicuj wykresy funkcji f i funkcji g.

2. ustal, jakim wzorem jest określona funkcja g.

Zadanie 6. (4 pkt.)

Wyznacz zbiór wszystkich argumentów, dla których funkcja f określona wzorem
przyjmuje wartości z przedziału
.

Czy do tego zbioru należy 0,75?

Zadanie 7. (4 pkt.)

Funkcja f jest określona wzorem

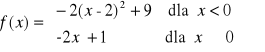
1. Narysuj wykres funkcji

2. Wyznacz miejsca zerowe.

3. W jakim zbiorze funkcja przyjmuje wartości dodatnie.

Zadanie 8. (3 pkt.)

Wyznacz dziedzinę funkcji f jeżeli:
.

Zadanie 9. (4 pkt.)

Wyznaczyć trójmian kwadratowy
wiedząc, że jego wykres przechodzi przez punkty (0;1), (1;-2) oraz, że dla
osiąga swoją najmniejszą wartość.

Zadanie 10. (7 pkt.)

Trzej robotnicy wykonali pewną pracę w x dni. Pierwszy z nich pracując samodzielnie wykonałby tę pracę w czasie o 6 dni dłuższym, drugi w czasie o 18 dni dłuższym, trzeci w czasie cztery razy dłuższym. Obliczyć x.

Zadanie 11. (5 pkt.)

Dla jakich wartości parametru m równanie
ma dwa różne pierwiastki mniejsze niż 4.

Zadanie 12. (7 pkt.)

Dana jest funkcja kwadratowa w postaci kanonicznej

1. Przedstaw tę funkcję w postaci ogólnej i iloczynowej

2. Narysuj wykres tej funkcji

3. Podaj zbiór wartości funkcji, zbiór w którym funkcja jest rosnąca, zbiór tych argumentów, dla których funkcja przyjmuje wartości nieujemne.

Zadanie 13. (4 pkt.)

Rozwiąż graficznie nierówność:
.

Zadanie 14. (5 pkt.)

Funkcja kwadratowa
ma dwa miejsca zerowe:
,
.

1. Wyznacz b oraz c.

2. Podaj postać kanoniczną tej funkcji.

3. Narysuj wykres tej funkcji.

Zadanie 15. (3 pkt.)

Równanie
można rozwiązać w następujący sposób:

Wykorzystując wskazany sposób rozwiąż równanie:

Schemat punktowania - funkcja kwadratowa

Poziom podstawowy

Numer zadania	Etapy rozwiązania zadania	Liczba punktów
1.	Zapisanie warunków zadania kolejne liczby x, y, z Warunki zadania	1
		Wyznaczenie x;	1
		Zapisanie funkcji argumentu, jako suma kwadratów kolejnych liczb. Przekształcenie wzoru do prostszej postaci.	2
		Stwierdzenie, że f jako funkcja kwadratowa o dodatnim współczynniku przyjmuje wartość najmniejszą dla	1
		Obliczenie y, z oraz zapisanie odpowiedzi , ,	1
	2.	Uzależnienie współczynników b i c od a oraz różnicy ciągu i zapisanie trójmianu w postaci	1
		Stwierdzenie faktu, że reszta z dzielenia trójmianu przez dwumian jest równa , z tego wynika	1
		Obliczenie a, b, c zapisanie wzoru trójmianu i napisanie równania osi symetrii paraboli	1
		Obliczenie wartości największej i najmniejszej w przedziale	1
	3.	Wyznaczenie dziedziny i na jej podstawie wyznaczenie przyprostokątnych i przeciwprostokątnej	1
		Skorzystanie z twierdzenia Pitagorasa i obliczenie	1
		Obliczenie pola trójkąta (24j^2)	1
	4.	Wyznaczenie dziedziny	1
		Zapisanie warunków trójkąta	1
		Rozwiązanie warunków trójkąta	2
		Wyznaczenie odpowiedzi	1
	5.	Rysunek funkcji f	1
		Rysunek funkcji g	1
		Ustalenie wzoru funkcji	1
	6.	Zapisanie układu nierówności	1
		Rozwiązanie układu i wyznaczenie zbioru argumentów	2
		Sprawdzenie czy 0,75 należy do tego zbioru i sformułowanie odpowiedzi	1
	7.	Rysunek funkcji f	1
		Wyznaczenie miejsc zerowych	2
		Wyznaczenie zbioru argumentów dla których funkcja przyjmuje wartości dodatnie wartości	1
	8.	Zapisanie warunków zadania	1
		Rozwiązanie układu nierówności	1
		Sformułowanie odpowiedzi	1
	9.	Wyznaczenie warunków zadania	2
		Rozwiązanie układu równań	1
		Zapisanie odpowiedzi	1
	10.	Zapisanie ile pracy wykonuje każdy pracownik jednego dnia np. 1 robotnik całej pracy, drugi ……, trzeci	2
		Ułożenie równania sumy pracy wykonywanej przez robotników w ciągu jednego dnia	2
		Doprowadzenie równania do postaci	1
		Rozwiązanie równania	1
		Sformułowanie prawidłowej odpowiedzi (sprawdzenie czy pierwiastki SA rozwiązaniami)	1
	11.	Zapisanie warunków zadania	2
		Rozwiązanie układu nierówności	2
		Sformułowanie poprawnej odpowiedzi	1
	12.	Sprowadzenie wzoru funkcji do postaci ogólnej	1
		Sprowadzenie funkcji do postaci iloczynowej	2
		Naszkicowanie wykresu funkcji	1
		Odczytanie zbioru wartości funkcji	1
		Odczytanie przedziału, w którym funkcja jest rosnąca	1
		Odczytanie zbioru tych argumentów , dla których funkcja przyjmuje wartości nieujemne	1
	13.	Narysowanie wykresu funkcji	1
		Narysowanie wykresu funkcji	1
		Odczytanie z wykresu odciętych punktów wspólnych obu wykresów -2,1	1
		Odczytanie z wykresu , dla jakich argumentów wartości funkcji f(x) są mniejsze bądź równe od wartości funkcji g(x) Odp.	1
	14.	Wyznaczenie współczynników	2
		Sprowadzenie wzoru funkcji do postaci kanonicznej:	2
		Naszkicowanie wykresu funkcji	1
	15.	Doprowadzenie równania do postaci:	1
		Doprowadzenie równania do postaci:	1
		Rozwiązanie równania	1

Funkcja kwadratowa

21

---