WŁASNOŚCI FUNKCJI

Poziom podstawowy

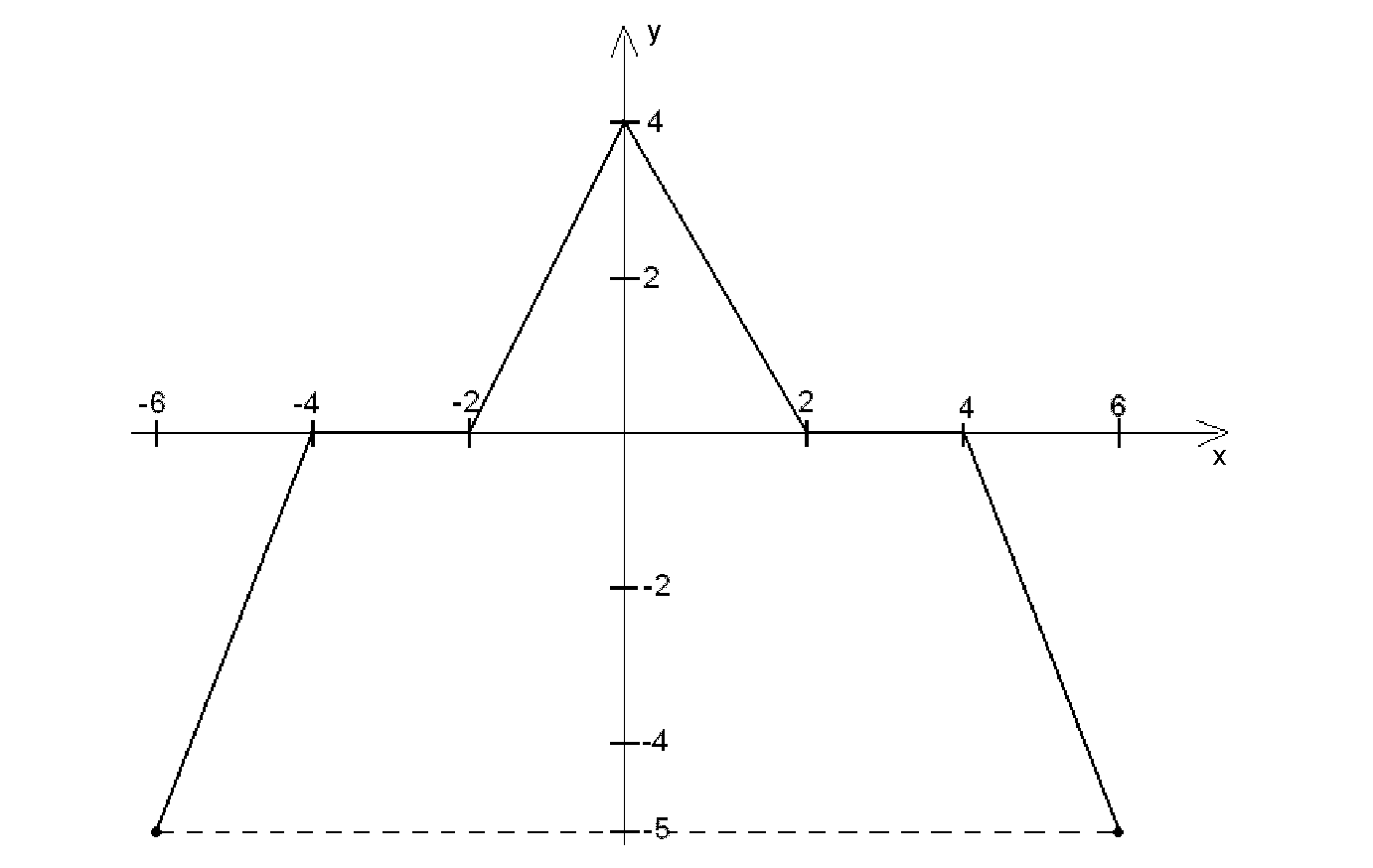
Zadanie 1. (5 pkt.)

Dany jest wykres funkcji f:

1. Wyznacz równanie opisujące funkcję f.

2. Wyznacz przedziały monotoniczności funkcji f.

3. Dla jakich argumentów funkcja f przyjmuje wartości ujemne, dla jakich dodatnie.

4. Podaj wartość najmniejszą oraz największą funkcji f.

Zadanie 2. (6 pkt.)

Dany jest wykres funkcji g:

1. Opisz funkcję g równaniem algebraicznym.

2. Wyznacz dziedzinę oraz zbiór wartości funkcji g.

3. Wyznacz miejsca zerowe funkcji g.

4. Dla jakich argumentów funkcja g przyjmuje wartości dodatnie, dla jakich ujemne?

5. Podaj wartość największą oraz najmniejszą funkcji g.

Zadanie 3. (7 pkt.)

Dany jest wzór funkcji:

1. Sporządź wykres funkcji f.

2. Wyznacz dziedzinę oraz zbiór wartości funkcji f.

3. Podaj wartość najmniejszą oraz największą funkcji f.

4. Dla jakich argumentów funkcja przyjmuje wartości dodatnie, a dla jakich ujemne?

Zadanie 4. (4 pkt.)

Dany jest zwór funkcji f:

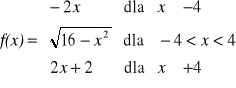
1. Sporządź wykres funkcji f.

2. Podaj miejsca zerowe funkcji.

3. Wyznacz przedziały monotoniczności funkcji.

Zadanie 5. (8 pkt.)

Dana jest funkcja
.

1. Napisz równanie prostej prostopadłej oraz równoległej do f i przechodzącej przez punkt
   .

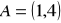
2. Wyznacz współrzędne punktu A' będącego obrazem punktu A w symetrii osiowej względem prostej o równaniu f.

3. Napisz wzór funkcji, której wykres powstaje z przekształcenia f w symetrii osiowej względem osi OX oraz osi OY.

4. Narysuj w jednym układzie współrzędnych wykres funkcji f oraz wykresy otrzymanych funkcji.

5. Oblicz odległość punktu
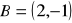
   leżącego na wykresie funkcji f od punktu A.

Zadanie 6. (3 pkt.)

Dana jest funkcja zadana według przepisu:

1. Wyznacz dziedzinę oraz zbiór wartości funkcji.

2. Dla jakich argumentów funkcja przyjmuje wartość 12.

3. Sporządź wykres funkcji w układzie współrzędnych.

Zadanie 7. (5 pkt.)

Funkcja liczbowa określona jest następująco:

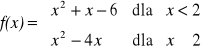
1. Oblicz wartość funkcji f odpowiednio dla argumentów
   .

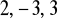
2. Sprawdź, która z liczb
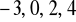
   jest miejscem zerowym funkcji f.

3. Wyznacz te argumenty, dla których funkcja f przyjmuje wartość - 4.

4. Sporządź wykres funkcji f.

Zadanie 8. (3 pkt.)

Dany jest wykres funkcji:

1. Określ dziedzinę oraz zbiór wartości funkcji.

2. Podaj przedziały monotoniczności funkcji.

3. Czy wykres funkcji posiada oś symetrii? Jeżeli tak, to podaj jej równanie.

Zadanie 9. (Punktacja nie dotyczy tego zadania.)

Ćwiczenia wprowadzające:

1. Sporządź wykresy funkcji:

,
,
,
,

2. Rozwiąż równanie:

,
,
,
,
,
,
,
,

3. Rozwiąż nierówność:

,
,
,
,
,
,

4. Na płaszczyźnie OXY narysuj zbiory A i B, gdzie:

Zaznacz na płaszczyźnie OXY następujące zbiory:

,
,
,
,
,

Schemat punktowania - własności funkcji

Poziom podstawowy

Numer zadania	Etapy rozwiązania zadania	Liczba punktów
1.	Wyznaczenie równania opisującego funkcję f- kawałki funkcji liniowych wyznaczonych na odpowiednich przedziałach.	2
		Wyznaczenie przedziałów monotoniczności funkcji f f rośnie dla , f maleje dla , f jest stała dla lub inna klasyfikacja - f jest niemalejąca dla , f jest nierosnąca dla	1
		f<0 dla , f> 0 dla	1
		Podanie wartości najmniejszej (-5) oraz największej (4) funkcji f	1
	2.	Wyznaczenie równania opisującego funkcję g- kawałki funkcji liniowych wyznaczonych na odpowiednich przedziałach	2
		Wyznaczenie dziedziny oraz zbioru wartości funkcji g-	1
		Miejsca zerowe x=-6 lub x=0	1
		g<0 dla , g> 0 dla	1
		Podanie wartości najmniejszej (-3)oraz największej (6) funkcji g	1
	3.	Podpunkt a) Sporządzenie wykresu funkcji f	4
		Podpunkt b) D=R, W=	1
		Podpunkt c) wartość najmniejsza , wartość największa brak ( )	1
		Podpunkt d) f>0 dla	1
	4.	Podpunkt a) Sporządzenie wykresu funkcji f	2
		Podpunkt b) brak miejsc zerowych (potencjalne miejsca zerowe nie należą do D)	1
		Podpunkt c) f maleje dla , f rośnie dla	1
	5.	Podpunkt a) prosta równoległa y=-2x+6, prosta prostopadła y = 0.5x+3.5	2
		Podpunkt b)	3
		Podpunkt c) symetria względem osi OX y=2x-3, względem osi OY y=2x+3	1
		Podpunkt d) Narysowanie wykresu funkcji f oraz wykresów otrzymanych funkcji	1
		Podpunkt e) Odległość	1
6.	Za każdy podpunkt po 1 punkcie. Podpunkt a) D={1,2,3,4,5,6,7,8,9,10,11}, W={-3,0,5,12,21,32,45,60,77,96,117} Podpunkt b) funkcja przyjmuje wartość 12 dla argumentu x=4 Podpunkt c) Sporządzenie wykresu funkcji	3
7.	Podpunkt a) f(2)= -4, f(-3) = 0, f(3)=-3	1
		Podpunkt b) miejsca zerowe to x=4 lub x=-3	1
		Podpunkt c) f=-4 dla x=-2 lub x=1 lub x=2	1
		Podpunkt d) Sporządzenie wykresu funkcji f	2
	8.	Podpunkt a) D=R , W=	1
		Podpunkt b) funkcja rośnie dla , f maleje dla	1
		Podpunkt c) oś symetrii funkcji f - x=0	1
9.	Zadanie traktujemy jako ćwiczenia wprowadzające, przypominamy definicję wartości bezwzględnej oraz działania na zbiorach.	Nie dotyczy

Własności funkcji

7

---