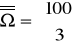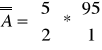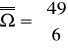RACHUNEK PRAWDOPODOBIEŃSTWA

I STATYSTYKA

Poziom podstawowy

Zadanie 1. (4 pkt.)

Rzucono monetą i kostką sześcienną do gry. Niech A oznacza zdarzenie: wypadł orzeł i parzysta liczba oczek, B - wypadł orzeł i liczba oczek podzielna przez 3. Oblicz prawdopodobieństwo zdarzeń A, B,
.

Zadanie 2. (3 pkt.)

Jakie jest prawdopodobieństwo, że ustawiając dwie dziewczyny i pięciu chłopców w rzędzie, dziewczęta nie będą stały obok siebie?

Zadanie 3. (3 pkt.)

W pewnej loterii na 100 losów 5 jest wygrywających. Oblicz prawdopodobieństwo, że wśród 3 kupionych losów tej loterii 2 są wygrywające i 1 przegrywający.

Zadanie 4. (5 pkt.)

Wypełniamy jeden zakład w Dużym Lotku (6 z 49). Jakie jest prawdopodobieństwo trafienia szóstki, a jakie piątki?

Zadanie 5. (5 pkt.)

Z talii 52 kart losujemy cztery karty. Oblicz prawdopodobieństwo wylosowania:

1. kart tego samego koloru;

2. czterech asów;

3. dwóch dam i dwóch królów;

4. trzech dziesiątek i jednej czwórki;

5. kart różnych kolorów.

Zadanie 6. (4 pkt.)

Rzucamy cztery razy symetryczną monetę. Oblicz prawdopodobieństwo:

1. że orzeł wypadnie parzystą ilość razy;

2. że na pierwszych dwóch monetach wypadnie reszka;

3. że reszka wypadnie, co najmniej dwa razy;

4. że orzeł wypadnie, co najwyżej 3 razy.

Zadanie 7. (8 pkt.)

Wypisz wszystkie znane ci własności prawdopodobieństwa. Przy danych:

1. 
   ,
   ,
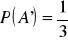
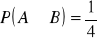
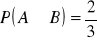
   , oblicz: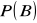
   ,
   ,
   

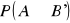
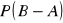
b)
,
,
, oblicz:
,
,
,

c)
,
,
oblicz:
,

d)
,
,
oblicz:
,

Zadanie 8. (4 pkt.)

Z grupy osób, w której jest 5 kobiet i 4 mężczyzn wybieramy trzyosobową delegację. Jakie jest prawdopodobieństwo, że w skład delegacji wejdą:

1. co najwyżej dwie kobiety

2. co najmniej 1 mężczyzna

3. dokładnie 2 kobiety

Zadanie 9. (7 pkt.)

Z pudełka, w którym znajdują się kartki z cyframi:1, 2, 3, 4, 5, 6, 7, 8, 9 losujemy 3 razy po jednej kartce bez zwrotu i tworzymy z otrzymanych cyfr liczbę trzycyfrową, której cyfrą setek jest pierwsza z wylosowanych liczb, dziesiątek - druga, jedności - trzecia.

Oblicz prawdopodobieństwo, że otrzymana liczba jest:

1. parzysta

2. podzielna przez 4

Zadanie 10. (7 pkt.)

Uczeń, w ciągu roku szkolnego otrzymał z pewnego przedmiotu następujące oceny: 2, 2, 3, 4, 5, 5, 3, 3, 1, 4, 3, 3, 2, 4.

Oblicz:

1. Rozstęp dla danych;

2. Średnią arytmetyczną;

3. Wariancję oraz odchylenie standardowe;

4. Modę oraz medianę;

5. Sporządź histogram liczebności dla powyższych danych.

Zadanie 11. (6 pkt.)

W bibliotece szkolnej badano, ile książek wypożyczają uczniowie w ciągu miesiąca. W tym, celu zbadano liczbę wypożyczonych przez losowo wybranych 32 uczniów książek i otrzymano: 1, 5, 0, 4, 8, 2, 0, 2, 1, 1, 3, 0, 2, 2, 3, 3, 4, 6, 2, 3, 5, 2, 0, 0, 1, 4, 2, 1, 0, 0, 0, 2.

1. Uporządkuj dane i oblicz rozstęp.

2. Przedstaw dane na diagramach liczebności i częstości względnych.

3. Oblicz modę i medianę dla danych.

Zadanie 12. (6 pkt.)

Dana jest tabela wyników (szereg rozdzielony):

Wartość	Liczebność
	3
	5
	7
	4

1. Oblicz średnią arytmetyczną
   .

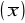
2. Oblicz wariancję i odchylenie standardowe
   .

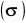
3. Jaki procent wyników należy do przedział
   .

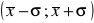
Zadanie 13. (3 pkt.)

Nauczycielka matematyki w klasie Janka ocenia w semestrze prace w następujących kategoriach:

- kartkówka (z wagą 20)

- praca domowa i odpowiedź ustna (z wagą 15)

- praca na lekcji (z wagą 10)

- sprawdzian (z wagą 40)

Na semestr proponuje ocenę x, jeżeli średnia ważona ocen znajduje się w przedziale
,
. Czy Jacek ma szansę mieć na semestr ocenę dobrą, jeśli dotychczas uzyskał w wymienionych kategoriach oceny: 2, 3, 4, 4, a może zdobyć jeszcze tylko jedną ze sprawdzianu? Na jaka ocenę musiałby zaliczyć ten sprawdzian?

Schemat punktowania - rachunek prawdopodobieństwa

i statystyka

Poziom podstawowy

Numer zadania	Etapy rozwiązywania zadania	Liczba punktów
1.	Obliczenie mocy zbioru Ω	1
		Obliczenie	1
		Obliczenie	1
		Obliczenie	1
	2.	Obliczenie mocy zbioru Ω : 7!	1
		Obliczenie liczby ustawień, gdzie dziewczyny nie stoją obok siebie (od wszystkich możliwych ustawień odejmiemy te, gdzie dziewczyny stoją obok siebie)	1
		Obliczenie szukanego prawdopodobieństwa :	1
	3.	Obliczenie	1
		Obliczenie	1
		Obliczenie	1
	4.	Obliczenie	1
		Obliczenie par trafienia szóstki ,	2
		Obliczenie Pr-a trafienia piątki ,	2
5.	Każdy podpunkt zadania	1
6.	Każdy podpunkt zadania	1
7.	Każdy podpunkt zadania (wskazane diagramy Venna w niektórych przypadkach)	1
8.	Zapisanie przestrzeni zdarzeń elementarnych (Zbiór wszystkich trzyelementowych podzbiorów zbioru 9 osób)	1
		Obliczenie prawdopodobieństwa zdarzenia A'- w skład delegacji wejdą trzy kobiety, a następnie prawdopodobieństwa zdarzenia A	1
		Zauważenie, że	1
		Obliczenie	1
	9.	Zapisanie przestrzeni zdarzeń elementarnych (Zbiór wszystkich trójelementowych ciągów o wyrazach ze zbioru 1, 2, 3, 4, 5, 6, 7, 8, 9 przy czym wyrazy ciągu nie mogą się powtarzać	1
		Obliczenie liczby zdarzeń elementarnych (mocy omega)	1
		Obliczenie liczby zdarzeń sprzyjających zdarzeniu z pkt.a 4	2
		Obliczenie liczby zdarzeń sprzyjających zdarzeniu z pkt.b	2
		Obliczenie prawdopodobieństw	1
	10.	Rozstęp dla danych	1
		Średnia arytmetyczna	1
		Wariancja oraz odchylenie standardowe;	2
		Moda oraz mediana;	2
		Histogram liczebności dla danych	1
	11.	Uporządkowanie i rozstęp	2
		Diagramy liczebności i częstości względnych	2
		Moda oraz mediana	2
	12.	Średnia arytmetyczna	2
		Wariancja i odchylenie standardowe	2
		Procent wyników	2
	13.	Obliczenie średniej ważonej przy ocenie ze sprawdzianu 6 oraz 5	1
		Obliczenie średniej ważonej przy ocenie ze sprawdzianu 4 i stwierdzenie ,że niższe oceny ze sprawdzianu jeszcze zmniejszają średnią	1
		Sformułowanie odpowiedzi	1

Rachunek prawdopodobieństwa i statystyka

48