Ćwiczenie 2

1. Miary poziomu

Średnie

Przykład 1

Obliczyć następujące parametry zbiorowości statystycznej, wymienionej w przykładzie 1 Ćwiczenie 1:

1. Średnia arytmetyczna m_a:

1. na podstawie szeregu szczegółowego;

=
=

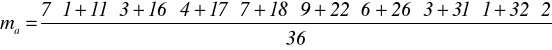
= 19,167.

2. na podstawie rozkładu przedziałowego.

=
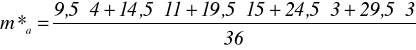
= 18,1.

Przykład 2

2. Średnia geometryczna m_g:

3. na podstawie szeregu szczegółowego;

= 18,357.

4. na podstawie rozkładu przedziałowego.

= 17,349.

Przykład 3

3. Średnia harmoniczna m_h:

1. na podstawie szeregu szczegółowego;

=
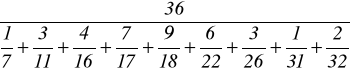
= 17,474.

2. na podstawie rozkładu przedziałowego.

=
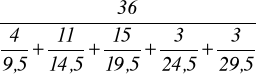
= 16,567.

Miary położenia pozycyjne

Przykład 4

4. Mediana Me:

1. na podstawie szeregu szczegółowego;

szereg statystyczny składa się z parzystej liczby jednostek statystycznych,

n = 36,

= 18,
= 19.

Zatem

Me =
=
= 18.

2. na podstawie rozkładu przedziałowego.

r = 3, x_r = 17, n = 36, d_r = 5,

f₁ = 4, f₂ = 11, f₃ = 15,

Me* = 17 +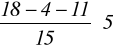
= 18.

Przykład 5

5. Kwartyl pierwszy Q₁:

1. na podstawie szeregu szczegółowego;

pierwsza połowa szeregu statystycznego składa się z parzystej liczby k = 18 jednostek statystycznych, zatem

k = 18,

= 9,
= 10.

Zatem

Q₁ =
=
= 17.

2. na podstawie rozkładu przedziałowego.

r(1,4) = 2, x_d(1,4) = 12, n = 36, h_r(1,4) = 5;

f₁ = 4, f₂ = 11;

Q*₁ = 12 +
= 14,2727.

Przykład 6

6. Kwartyl trzeci Q₃:

1. na podstawie szeregu szczegółowego;

druga połowa szeregu statystycznego składa się z parzystej liczby k = 18 jednostek statystycznych, zatem

k = 18,

= 9,
= 10.

Q₃ =
=
= 22.

2. na podstawie rozkładu przedziałowego.

r(3,4) = 3, x_d(3,4) = 17, n = 36, h_r(1,4) = 5;

f₁ = 4, f₂ = 11, f₃ = 15;

Q*₃ = 17 +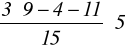
= 21.

Przykład 7

7. Dominanta Mo:

1. na podstawie szeregu szczegółowego;

max{f₁, f₂, … f_k} = 9,

x_i* = x₅ = 18,

Mo = 18.

2. na podstawie rozkładu przedziałowego.

rD = 3, x_rD = 17, h_rD = 5,

f_rD-1 = 11, f_rD = 15, f_rD+1 = 3,

Mo* = 17 +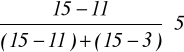
= 18,25.

1

---