Moment bezwładności, miara bezwładności ciała w ruchu obrotowym. Charakteryzuje rozkład masy w ciele. Moment bezwładności ciała względem osi z nazywane jest wyrażenie:
gdzie mi - masy elementów ciała odległe każda o ri od osi z
Dla ciągłego rozkładu masy w ciele sztywnym moment bezwładności definiowany jest wzorem całkowym:
gdzie: ρ - funkcja opisująca gestość ciała, V - objętość ciała, dV - element objętości, r - odległość elementu dV od osi z.
Energia w ruchu obrotowym ciała sztywnego opisana jest wzorem: E=(I2)/2. Moment bezwładności względem osi z' równoległej do z, odległej od niej o D wyraża się wzorem:
Iz=Iz'+MD2
gdzie: M - masa ciała, jest to tzw. twierdzenie Steinera, podane przez matematyka szwajcarskiego J. Steinera.
Zdefiniowane powyżej momenty bezwładności są wielkościami skalarnymi, w ogólnym przypadku moment bezwła dności jest tensorem trzeciego rzędu, wyrazy na przękątnej (w reprezentacji macierzowej tensora) są momentami bezwładności obliczonymi względem trzech wzajemnie prostopadłych osi przedmiotu, np.:
lub - dla ciągłego rozkładu masy - odpowiedni wzór całkowy), wyrazy poza przekątną nazywane momentami odśrodkowymi zdefiniowane są następująco (lub przez odpowiednie wzory całkowe):
Względności teoria szczególna, STW, teoria fizyczna, której zręby przedstawił A. Einstein w pracy O elektrodynamice ciał w ruchu (1905). W kolejnych pracach Einstein opracował zgodne z nową teorią zasady mechaniki tworząc tym samym fizykę relatywistyczną. Elektrodynamika opisana równaniami Maxwella zgodna była z teorią względności.
Podstawowe założenie STW to stałość prędkości światła w każdym układzie odniesienia (Michelsona-Morleya doświadczenie) - wynika z tego prawo transformacji współrzędnych przestrzennych i czasu przy przejściu od jednego układu odniesienia do drugiego opisane przez transformację Lorentza, oraz postulat prawdziwości zasady względności głoszącej, że prawa fizyki mają taką samą postać w każdym inercyjnym układzie odniesienia.
Einstein wykorzystał wprowadzony przez H. Poincarego i udoskonalony przez H. Minkowskiego formalizm czterowymiarowej płaskiej czasoprzestrzeni. Elementem rewolucyjnym było nadanie fizycznej realności prawu przekształcającemu przy zmianie układu odniesienia, oprócz współrzędnych przestrzennych, również czas (wcześniej traktowano je czysto formalnie). Przestrzeń przestała tak pełnić rolę obiektywnej "sceny" zjawisk przyrody, a czas stracił swoją absolutność - stały się one względne, zależne od układu odniesienia, gdyż zgodnie z STW dwa zdarzenia równoczesne w pewnym układzie odniesienia nie muszą być równoczesne w innym.
W STW energia i pęd cząstki tworzą czterowektor, dla cząstki swobodnej spełniony jest związek (E/c)2 = p2 + m2c2, gdzie m - masa cząstki. Dla cząstki spoczywającej, tj. przy p = 0 wzór ten sprowadza się do wyrażenia E=m0c2, które interpretuje się jako równoważność masy i energii.
Prawa STW przechodzą w prawa klasycznej fizyki, gdy prędkość światła w próżni zmierza do nieskończoności.
Ruch, jedno z podstawowych pojęć fizyki. Oznacza przemieszczanie się elementów układu fizycznego względem układu odniesienia (ruch jest zawsze względny). Zjawisko ruchu rozpatruje się najczęściej w odniesieniu do inercjalnego układu odniesienia. Klasyfikuje się je na wiele sposobów.
Podstawowym rodzajem ruchu jest ruch postępowy - zachodzi on, gdy prosta łącząca dwa dowolne punkty układu jest równoległa do prostej łączącej te same punkty ciała w każdej innej chwili trwania ruchu. Innym ważnym rodzajem jest ruch obrotowy.
Ze względu na własności kinematyczne ruch dzieli się na prostoliniowy, krzywoliniowy itp. Ze względu na własności dynamiczne ruch w inercjalnych układach odniesienia dzieli się na jednostajny, niejednostajny, jednostajnie przyspieszony i niejednostajnie przyspieszony.
W ruchu jednostajnym prędkość jest stała, a przebyta droga równa iloczynowi czasu trwania ruchu i prędkości, w ruchu jednostajnie przyspieszonym chwilowa prędkość u jest proporcjonalna do czasu t:
u = at,
gdzie a - przyspieszenie (w ruchu opóźnionym a < 0), natomiast droga s określona jest wzorem
s=uot+at2/2,
gdzie uo - prędkość początkowa. Dla ruchu niejednostajnego:
.
Kondensacja, 1) zagęszczenie, stężenie czegoś.
2) nadanie czemuś zwartego układu, zwięzłe ujęcie, przedstawienie.
3) w chemii reakcja między dwoma lub większą ilością cząstek, w której wyniku powstaje nowa cząstka o większym ciężarze i wydziela się prosty związek chemiczny (np. woda, alkohol, wodór).
4) w fizyce przemiana fazowa gazu w ciecz, możliwa jedynie w temperaturach mniejszych od krytycznej temperatury. Zachodzi dzięki ochłodzeniu lub izotermicznemu sprężeniu gazu.
Carnota cykl, uproszczony, zamknięty cykl przemian termodynamicznych wyidealizowanego, odwracalnego, quasi-statycznego silnika cieplnego. Składa się z dwóch izoterm i dwóch izobarów.
Silnik działający zgodnie z cyklem Carnota składałby się ze ścianek cylindra i tłoka wykonanych z doskonałego izolatora ciepła i zamkniętego dnem cylindra, będącego idealnym przewodnikiem ciepła. Dno kontaktowałoby się kolejno - z izolatorem ciepła (podczas sprężania adiabatycznego), zbiornikiem ciepła o wyższej temperaturze (rozprężanie izotermiczne), izolatorem ciepła (rozprężanie adiabatyczne) i zbiornikiem ciepła o niskiej temperaturze-chłodnicy (sprężanie izotermiczne).
Przemiany w cyklu Carnota zachodzące w odwrotnym kierunku zamieniają silnik w maszynę chłodniczą lub tzw. pompę cieplną.
Prędkość kosmiczna, progowa prędkość umożliwiająca osiągnięcie pewnego rodzaju orbity (prędkość orbitalna). Wyróżnia się:
- pierwszą prędkość kosmiczną, odpowiadającą prędkości niezbędnej do umieszczenia ciała na niskiej, kołowej orbicie wokółziemskiej (wynosi ona 7,91 km/s),
- drugą prędkość kosmiczną, równą prędkości potrzebnej do umieszczenia ciała na geocentrycznej orbicie parabolicznej (tj. prędkości wystarczającej do opuszczenia pola grawitacyjnego Ziemi, wynosi ona 11,19 km/s).
Niekiedy mówi się też o trzeciej prędkości kosmicznej, tj. prędkości, jaką trzeba nadać ciału w pobliżu Ziemi, by opuściło ono Układ Słoneczny (wynosi ona 42 km/s w układzie odniesienia względem Słońca).
Dipol elektryczny, układ dwóch różnoimiennych ładunków elektrycznych znajdujących się względem siebie w pewnej skończonej odległości.
Potencjał, w fizyce funkcja skalarna lub wektorowa, związana z funkcją opisującą pewne pole fizyczne za pomocą operatorów różniczkowych (gradient, rotacja).
W mechanice definiuje się skalarny potencjał siły V (wyrażamy w jednostkach energii), który związany jest z danym polem sił związkiem: F=-gradV, np. potencjał sił sprężystości:
V=-1/2k2x2
gdzie: k - stała sprężystości, x - odkształcenie, lub potencjał grawitacyjny:
gdzie: m i M - masy przyciągających się ciał, G - stała grawitacji, r - wzajemna odległość środków ciała.
W elektrodynamice określa się skalarny potencjał elektrostatyczny i wektorowy potencjał pola elektromagnetycznego A (tworzą czterowektor). Są one związane z wektorami natężenia pola elektrycznego E i magnetycznego H równościami:
gdy A nie jest funkcją czasu druga z równości opisuje pole elektrostatyczne.
Ogólne pojęcie potencjału wykorzystywane jest w termodynamice (potencjał termodynamiczny), duże znaczenie ma również w fizyce kwantowej (równanie Schrödingera). Minima funkcji potencjału sił wyznaczają położenia równowagi trwałej, maksima odpowiadają położeniom równowagi chwiejnej.
Powierzchnie o jednakowych wartościach potencjału skalarnego noszą nazwę powierzchni ekwipotencjalnych. Potencjał może określać dostępną dla cząstki o danej energii przestrzeń (bariera potencjału)
PRAWA DYNAMIKI jeżeli na ciało nie działa jakakolwiek siła lub siły się równoważą to ciało porusza się ruchem jednostajnym po lini prosteej lub pozostaje w spoczynku F=0 , V=const, lub V=0.. 2 zasada dynamiki-jeżeli na ciało działa siła niezrównoważona to ciało porusza się ruchem jednostajnnie zmiennym z a wprostproporcjon do działającej siły i odwrotnie proporcjonal do masy ciała. Kierunek i zwrot „a” jest zgodny z kierunkiem i zwrotem wypadkowej siły F≠0⇒V=CONST a=F/m, to pęd (wektoro) p=m*v, F=dp/dt⇒p-p0=∫Fdt⇒zasada zach pędu
3 zasada dynamiki-jeżeli ciało A działa na ciało B siłą FAB to w tej samej chwili ciało B oddziałuje na ciało A siłą FBA. siły mają tą samą wartość ten sam kierunek działania siły ,lecz zwroty są przeciwne. Siły przyłożone są do różnych ciał FAB= -FBA każdej akcji towarzyszy reakcja
Moment pędu, kręt, wektor osiowy J charakteryzujący ruch ciała (w szczególności ruch obrotowy): J=rp (iloczyn wektorowy wektora wodzącego r i pędu ciała).
Dla układu ciał moment pędu układu jest sumą wektorową momentu pędu pojedynczych ciał, dla ciała o ciągłym rozkładzie masy moment pędu wyraża się wzorem:
gdzie: V - objętość ciała, dv - element objętości, ρ(r) - funkcja rozkładu gęstości, u(r) - prędkość elementu objętości dv.
Równanie ruchu obrotowego ciała ma postać:
dJ/dt=D
gdzie D moment sił zewnętrznych (moment siły).
Monent pędu bryły sztywnej wyraża się (w układzie odniesienia, w którym oś obrotu przechodzi przez początek układu) poprzez tensor momentu bezwładności I i prędkość kątową , J=I. Monent pędu izolowanego układu jest zachowywany (zasada zachowania krętu).
W fizyce kwantowej moment pędu jest wielkością skwantowaną (kwantowanie), ponadto pojawia się wewnętrzny moment pędu (spin).
Lorentza transformacja, Lorentza przekształcenie, przekształcenie matematyczne opisujące transformacje wielkości fizycznych w czasoprzestrzeni czterowymiarowej przy przechodzeniu od jednego inercjalnego układu odniesienia, określonego przez współrzędne przestrzenne x, y, z i współrzędną czasową t, do drugiego, określonego przez współrzędne x', y', z' oraz t'.
W najprostszym przypadku, jeśli układ (x', y', z', t') porusza się jednostajnie w kierunku osi x z prędkością v, to transformacja Lorentza ma postać:
gdzie c - prędkość światła w próżni.
Często dla uproszczenia postaci zapisu transformacji do wzorów powyższych stosuje się podstawienie: =v/c oraz
a także mnoży się obustronnie przez c równanie opisujące transformację czasu dla uzyskania formalnej identyczności równań dla zmiennych: czasowej (równej ct) i przestrzennej x, wówczas: x'=γ(x-ct), y'=y, z'=z, ct'=γ(ct-x).
Z transformacji Lorentza wynikają wszystkie efekty kinematyczne szczególnej teorii względności, takie jak: reguła sumowania się prędkości prowadząca do niemożności uzyskania prędkości większej od prędkości światła, względność pojęcia równoczesności, skrócenie Lorentza-Fitzgeralda, spowolnienie biegu poruszajacych sie zegarów.
Równania transformacji Lorentza zostały opracowane ponad 10 lat przed sformułowaniem przez A. Einsteina szczególnej teorii wzgledności (zostały wywnioskowane z równań Maxwella), były jednak wówczas traktowane jako formalne równania matematyczne, bez konsekwencji fizycznych. Transformacja Lorentza uzupełniona obrotami w przestrzeni trójwymiarowej stanowi tzw. grupę przekształceń Poincarégo.
Dla małych prędkości v, rozwijając w szeregi potęgowe wzory opisujące transformację Lorentza, przy zaniedbaniu wyższych wyrazów, otrzymuje się klasyczne przekształcenie Galileusza. Transformacja Lorentza równoważna jest geometrycznie obrotowi w czterowymiarowej, zespolonej przestrzeni Minkowskiego o rzeczywistych osiach x,y,z, oraz urojonej osi czasowej (zmienna czasowa ma wówczas postać ict, gdzie i - jednostka urojona, c - prędkość światła w próżni).
W transformacji Lorentza niezmienną wielkością jest tzw. interwał czasoprzestrzenny określony jako: ds2=dx2+dy2+dz2-c2dt2. Transformacji Lorentza podlegają inne wielkości czterowektorowe, takie jak np. czterowektor enrgii-pędu. Wówczas do powyższych wzorów podstawia się zamiast czasu energię relatywistyczną cząstki podzieloną przez c, a składowe wektora położenia zastępuje się składowymi pędu. Wielkości tensorowe, spinorowe, itp. podlegają ogólnemu przekształceniu Lorentza, wyrażonemu bardziej złożonym układem równań.
Oddziaływanie grawitacyjne, grawitacja, ciążenie powszechne, jedno z fundamentalnych oddziaływań fizycznych. Zachodzi pomiędzy ciałami posiadającymi masę (masa grawitacyjna).
Klasyczna teoria grawitacji została opracowana przez I. Newtona w 1687. Teoria Newtona poprawnie opisuje słabe pola grawitacyjne. Ściślej zjawiska grawitacyjne opisuje einsteinowska ogólna teoria względności (OTW, 1916).
W ujęciu Newtona, w odległości r od ciała o masie M istnieje grawitacyjne pole potencjalne o potencjale danym skalarną funkcją:
=-grad GM/r
gdzie G grawitacji stała. Każde ciało posiadające masę umieszczone w tym polu nabywa przyspieszenie g dane wzorem
g = -grad
siła jaką działa ciało I (o masie M) na oddalone o r, ciało II (o masie m) wynosi
F=-gMmr/r3.
Zgodnie z III zasadą dynamiki Newtona identyczną co do wartości lecz przeciwnie skierowaną siłą działa ciało II na I.
Prawo powszechnego ciążenia jest uogólnieniem praw rządzących obrotem planet wokół Słońca. Newton odkrył je analizując prawa Keplera. Siły grawitacyjne są na ogół bardzo słabe, wg teorii Newtona oddziaływania grawitacyjne rozchodzą się z nieskończoną prędkością: zmiana położenia jakiegoś ciała wywołuje natychmiastową zmianę położeń wszystkich innych ciał we Wszechświecie, tego typu oddziaływanie jest niezgodne z postulatem teorii względności, który głosi, że maksymalną prędkością rozchodzenia się oddziaływań fizycznych jest prędkość światła c.
W ujęciu Einsteina siły grawitacyjne są analogiczne do sił bezwładności (tzw. zasada równoważności Einsteina). Zgodnie z tym przyspieszenie oraz siły grawitacyjne są efektem czysto geometrycznym, pojawiają się na skutek zakrzywienia przestrzeni. Podstawowymi pojęciami charakteryzującymi pole grawitacyjne w tym ujęciu są: tensor krzywizny Riemanna:
zastępujący siłę grawitacji i wyrażony przez symbole Christoffela oraz tensor metryczny g grający podobną rolę jak potencjał w ujęciu klasycznym.
Pierwszym sukcesem teorii Einsteina było wyjaśnienie tzw. nadwyżki ruchu peryhelium Merkurego oraz przewidywania potwierdzone obserwacyjnie dotyczące krzywoliniowego rozchodzenia się światła w polach grawitacyjnych. Trwają poszukiwania doskonalszej teorii grawitacji, uwzględniającej kwantową naturę pól fizycznych.
Pole magnetyczne-właściwośći przestrzeni polegająca na tym ze na poruszający się w niej ładunek elektryczny działa siła magnetyczna (lorentza F=q(B*V). Wartość natężenia pola magnetycznego wytworzonego przez nieskończenie długi prostoliniowy przewodnik jest wprost proporcjonalna do natężenia prądu I płynącego w tym przewodniku i odwrotnie proporcjonalna do odległości r od przewodnika
Właściwości magnetyczne -diamagnetyki (podatność magnetyczna <0 a względna przenikalność magnetyczna <1. diamagnetyki dają się niezwykle słabo namagnesować w kierunku przeciwnym do kierunku pola. Ciała diamagnetyczne są wypychane z obszary pola magnetycznego(bizmut, cynk , miedz,) -paramagnetyki substancje których podatność magnetyczna >0 a przenik magnetyczna względna >1magnesują się niezmiernie słabo zgodnie z kierunkiem pola. Ciała paramagnetyczne są wciągane w obszar pola magnetycznego(cyna chrom)-ferromagnetyki(podatność przybiera duże wartośći dodatnie a względna przenikalność >>1magnesują się 1000 razy silniej od paramagnetyków(żelazo)
PRAWO OERSTEDA-dotyczy indukowania się pola magnetycz wokół przewodnika z prądem.przy użyciu małej podpartej na ostrzu igiełki magnetycznej stanowiącej dipol magnetyczny o biegunach N i S. Jeśli do igiełki rozciągniemy przewodnik i przepuścimy prąd to igła zmieni swe ustawienie. obok działania składowej poziomej natężenia pola magnetycznego ziemskiego wystąpi moment pary sił pochodzących od pola magnetycznego prądu i skręcających igiełkę . kierunek wychylenia igły można wyznaczyć regułą prawej dłoni.
Pole elektrostatyczne, stacjonarne (nie ulega zmianom wraz z upływam czasu) pole elektryczne.
Pole elektrostatyczne opisuje wektor natężenia pola elektrycznego E lub potencjał tego pola , przy czym E = -grad , oraz wektor indukcji tego pola D = E, gdzie: - bezwględna przenikalność dielektryczna danego ośrodka.
Dla pola elektrostatycznego spełnione są ponadto równania divD = ρ i rotE = 0 (równania Maxwella ).
Maxwella równania, podstawowe równania klasycznej elektrodynamiki (J.C. Maxwell), opisujące związki pomiędzy natężeniami pola elektrycznego, magnetycznego i ładunkiem elektrycznym. Istnieje kilka równoważnych sformułowań równań Maxwella, najczęściej stosowane są formy różniczkowa lub całkowa równań Maxwella.
W postaci różniczkowej równania Maxwella wyrażają wzory:
div B=0
div D=bρ
gdzie: E - natężenie pola elektrycznego, H - natężenie pola magnetycznego, B =H - indukcja pola magnetycznego, - przenikalnośc magnetyczna ośrodka, j - gęstość prądu elektrycznego, D =E - indukcja pola elektrycznego, - przenikalność dielektryczna ośrodka (dielektryczna stała), ρ gęstość objętościowa ładunku elektrycznego, rot - operator rotacji, div - operator dywergencji, a i b - stałe uzgadniające jednostki, zależne od wyboru układu jednostek (np. w MKS i SI a=1= b, w układzie Gaussa a=1/c, b=4, gdzie c - prędkość światła w próżni).
W postaci całkowej równania Maxwella wyrażone są wzorami (w układzie jednostek SI):
gdzie: C - zamknięta krzywa ograniczająca powierzchnię S, prostopadłą do elementu przewodnika, V - dowolna powierzchnia zamknięta, n - wersor normalny do powierzchni, ds - element łuku krzywej C, dσ - element powierzchni, Q - całkowity ładunek elektryczny zawarty w przestrzeni ograniczonej powierzchnią V, I - natężenie prądu płynącego w przewodniku. Pozostałe oznaczenia jak we wzorach różniczkowych równań Maxwella.
Z pierwszego równania wynika prawo indukcji Faradaya (Faradaya zjawisko), drugie mówi o tym, że źródłami pola magnetycznego są zmienne pola elektryczne lub płynące prądy, trzecie równanie mówi o braku ładunków magnetycznych. Z czwartego równania wynika, że strumień pola elektrycznego przenikającego pewną powierzchnię jest proporcjonalny do ładunku elektrycznego zawartego w przestrzeni ograniczonej tą powierzchnią, z czego można wywnioskować prawo Coulomba.
Z równań Maxwella, uzupełnionych warunkami brzegowymi dla pól i prawami opisującymi zmianę pól na granicach nieciągłości ośrodków oraz równaniem na siłę Lorentza, można wyprowadzić wszystkie prawa elektrodynamiki klasycznej, ponadto z równań Maxwella dla pustej przestrzeni (j=0, ρ=0) Maxwell wywnioskował istnienie fal elektromagnetycznych (odkrytych później przez H. Hertza).
Z równań Maxwella wyprowadzono również formułę transformacji Lorentza.
Maxwella równania, podstawowe równania klasycznej elektrodynamiki (J.C. Maxwell), opisujące związki pomiędzy natężeniami pola elektrycznego, magnetycznego i ładunkiem elektrycznym. Istnieje kilka równoważnych sformułowań równań Maxwella, najczęściej stosowane są formy różniczkowa lub całkowa równań Maxwella.
W postaci różniczkowej równania Maxwella wyrażają wzory:
div B=0
div D=bρ
![]()
gdzie: E - natężenie pola elektrycznego, H - natężenie pola magnetycznego, B =H - indukcja pola magnetycznego, - przenikalnośc magnetyczna ośrodka, j - gęstość prądu elektrycznego, D =E - indukcja pola elektrycznego, - przenikalność dielektryczna ośrodka (dielektryczna stała), ρ gęstość objętościowa ładunku elektrycznego, rot - operator rotacji, div - operator dywergencji, a i b - stałe uzgadniające jednostki, zależne od wyboru układu jednostek (np. w MKS i SI a=1= b, w układzie Gaussa a=1/c, b=4, gdzie c - prędkość światła w próżni).
W postaci całkowej równania Maxwella wyrażone są wzorami (w układzie jednostek SI):
gdzie: C - zamknięta krzywa ograniczająca powierzchnię S, prostopadłą do elementu przewodnika, V - dowolna powierzchnia zamknięta, n - wersor
Z pierwszego równania wynika prawo indukcji Faradaya (Faradaya zjawisko), drugie mówi o tym, że źródłami pola magnetycznego są zmienne pola elektryczne lub płynące prądy, trzecie równanie mówi o braku ładunków magnetycznych. Z czwartego równania wynika, że strumień pola elektrycznego przenikającego pewną powierzchnię jest proporcjonalny do ładunku elektrycznego zawartego w przestrzeni ograniczonej tą powierzchnią, z czego można wywnioskować prawo Coulomba.
Z równań Maxwella, uzupełnionych warunkami brzegowymi dla pól i prawami opisującymi zmianę pól na granicach nieciągłości ośrodków oraz równaniem na siłę Lorentza, można wyprowadzić wszystkie prawa elektrodynamiki klasycznej, ponadto z równań Maxwella dla pustej przestrzeni (j=0, ρ=0) Maxwell wywnioskował istnienie fal elektromagnetycznych (odkrytych później przez H. Hertza).
Z równań Maxwella wyprowadzono również formułę transformacji Lorentza.
Obwód drgający, obwód elektryczny zawierający pojemność elektryczną C i indukcyjność własną L.
W obwodzie takim występują drgania o częstości kołowej:
Na skutek rozpraszania energii przez skończoną oporność obwodu drgania w rzeczywistych obwodach są drganiami gasnącymi, stopień wygasania charakteryzuje dobroć obwodu:
lub jej odwrotność, tzw. tłumienie d=1/Q.
Ciało doskonale czarne, ciało o współczynniku absorpcji równym jedności tzn., które niezależnie od temperatury całkowicie pochłania padające nań promieniowanie posiadające dowolny skład widmowy.
Ciało doskonale czarne jest pewną idealizacją, mającą duże znaczenie w teorii promieniowania. Przybliżoną jego realizacją jest otwór dużej wnęki sferycznej.
Prawa opisujące emisję promieniowania przez ciało doskonale czarne to prawa: Plancka, Wiena, Stefana-Boltzmanna.
Comptona efekt (zjawisko), rozpraszanie wysokoenergetycznego promieniowania elektromagnetycznego (gamma lub rentgenowskiego) na słabo związanych elektronach.
W wyniku rozpraszania elektron otrzymuje część pędu i energii padającego kwantu promieniowania, przez co rozproszony kwant promieniowania ma mniejszą energię (większą długość fali).
Zjawiska tego nie można wyjaśnić na gruncie klasycznej fizyki. Z analizy procesu zderzenia kwantu promieniowania z elektronem, gdy oba obiekty traktowane są jako sprężyste kulki, można otrzymać wzór na wzrost długości fali promieniowania:
= 2o(1-cos),
gdzie o tzw. comptonowska długość fali, - kąt rozproszenia. Jak widać zależy jedynie od czynników geometrycznych (nie zależy od energii), jest największa gdy cos = -1, a więc = 180 to znaczy, gdy padający foton rozproszy się do tyłu.
Uwzględnienie poprawki na energię wiązania elektronów w atomach zmienia przytoczony powyżej wzór dodając po prawej stronie równania czynniki D2, wprowadza więc zależność od energii promieniowania (D-stała dla danego materiału). Poprawka ta jest nieistotna, gdy energia promieniowania jest znacznie większa od energii wiązania elektronów.
Równanie stanu gazów rzeczywistych, równanie van der Waalsa, równanie postaci:
(p + an2/V2)( V-nb)=nRT,
gdzie: a, b - stałe charakterystyczne dla gazu, wyznaczane empirycznie na podstawie zależności:
a=27R2Tkr2/64pkr,
b=RTkr/8pkr,
gdzie: Tkr, pkr - temperatura i ciśnienie gazu w stanie krytycznym, V - objętość gazu, n - liczba moli gazu, R - stała gazowa, T - temperatura bezwzględna.
Równanie stanu gazów rzeczywistych daje lepsze przybliżenie rzeczywistej izotermy p(V) aniżeli równanie stanu gazów doskonałych, uwzględnia ponadto zjawisko skroplenia gazów i zjawiska krytyczne.
Półprzewodniki, substancje zachowujące się w pewnych warunkach jak dielektryk, a w innych jak przewodnik. Typowymi półprzewodnikami są: krzem, german, arsenek galu lub antymonek galu. Półprzewodniki mają małą szerokość pasma wzbronionego (teoria pasmowa).
Ze względu na typ przewodnictwa wyróżnia się półprzewodniki typu n - inaczej nadmiarowe (występuje tu przewodnictwo elektronowe, liczba elektronów w paśmie przewodnictwa przekracza liczbę dziur przewodzących w paśmie walencyjnym, uzyskuje się je przez domieszkowanie krzemu lub germanu pierwiastkami V grupy nazywanymi donorami) oraz typu p - inaczej niedomiarowe (występuje w nich przewodnictwo dziurowe w paśmie walencyjnym, liczba dziur przekracza liczbę elektronów w paśmie przewodnictwa, uzyskuje się je przez domieszkowanie krzemu lub germanu pierwiastkami III grupy nazywanymi akceptorami).
Odkrycie półprzewodników i wynalezienie licznych ich zastosowań spowodowało rewolucyjny postęp w elektronice (dioda półprzewodnikowa, tranzystor itd.).
Halla zjawisko (efekt), zjawisko powstania różnicy potencjałów U pomiędzy przeciwległymi ściankami półprzewodnika lub metalu w kierunku prostopadłym zarówno do kierunku przepływu prądu I, jak i do kierunku wektora indukcji zewnętrznego pola magnetycznego B.
Wartość napięcia wyrażona jest wzorem: U=A(BI)/d, gdzie: A jest tzw. stałą Halla, charakterystyczną dla danego rodzaju materiału, B jest wartością indukcji magnetycznej, d jest grubością płytki materiału.
Zjawisko Halla jest wynikiem odchylania w polu magnetycznym (Lorentza siła) elektronów tworzących przepływ prądu elektrycznego w metalu lub półprzewodniku. Jego zrozumienie miało duży wpływ na wyjaśnienie istoty zjawiska przepływu prądu elektrycznego. Nazwa efektu pochodzi od nazwiska jego odkrywcy (w 1879), fizyka amerykańskiego E.H. Halla (1855-1938).
Fajansa i Soddy'ego reguła, reguła określająca położenie pierwiastka powstałego po emisji cząstki lub z jądra macierzystego pierwiastka.
Emisja cząstki powoduje zmniejszenie masy jądra o cztery jednostki masy atomowej, a ładunku - o dwa ładunki elementarne, wskutek czego powstały pierwiastek znajduje się o dwa miejsca na lewo w układzie okresowym w stosunku do pierwiastka macierzystego. Emisja - powoduje przesunięcie położenia pierwiastka o jedno miejsce na prawo.
Obecnie reguła Fajansa i Soddy'ego obejmuje także emisję + (przesunięcie o jedno miejsce na lewo w układzie okresowym) - przemiana ta nie była znana, gdy formułowano pierwotną wersję reguły.
Jądro atomowe, centralna część atomu o rozmiarach rzędu 10-1410-15 m i gęstości ok. 1014g/cm3, zbudowana z Z (Z - atomowa liczba) protonów i A-Z (A to liczba masowa) neutronów (Nukleon). Zawiera w sobie praktycznie całą masę atomu, posiada ładunek elektryczny Ze. Istnienie jąder atomowych odkrył E. Rutherford (1911).
Jądro atomowe jest układem o skwantowanych, dozwolonych poziomach energetycznych. Jest układem związanym dzięki oddziaływaniom silnym jądrowym, które przezwyciężają odpychające oddziaływania elekrostatyczne protonów. W strukturze poziomów znaczący udział ma też niecentralna siła związana z oddziaływaniem spinów nukleonów.
Model kroplowy
W modelu kroplowym (N. Bohr, J.A. Wheeler) jądro atomowe traktowane jest jak kropla cieczy. Model ten pozwala w zarysie wyjaśnić energię wiązania i rozmiary jądra atomowego.
Schrödingera równanie, podstawowe równanie mechaniki kwantowej sformułowane w 1926 przez E. Schrödingera (zgodne z tzw. obrazem Schrödingera). Ogólnie Schrödingera równanie ma postać:
'
gdzie: i - jednostka urojona, h = h/2 (h - stała Plancka), t - czas, H - hamiltonian układu, - funkcja falowa opisująca ten układ.
Schrödingera równanie opisuje układy kwantowe przy pominięciu ich własności wynikających z ułamkowych wartości spinów cząstek oraz efektów relatywistycznych. Stosuje się je do opisu atomu wodoru, a także (w przybliżeniu) bardziej złożonych atomów oraz zjawisk kwantowych w kryształach. Schrödingera równanie opisujące niezależną od czasu radialną strukturę atomu wodoru ma postać:
gdzie: 2 - kwadrat operatora nabla, - masa zredukowana elektronu i jądra atomowego, U - energia potencjalna elektronu w polu elektromagnetycznym jądra, u - część funkcji falowej zależna jedynie od wzajemnego położenia elektronu i jądra, E - energia układu.
Rozwiązania tego równania, będące złożeniem wielomianów Laguerre'a (opisujących zależność radialną) i funkcji kulistych (opisujących zależności kątowe), odtwarzają z dobrym przybliżeniem strukturę atomu wodoru (m.in. poziomy energetyczne).
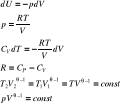
Liczby kwantowe, pojawiające się często przy rozpatrywaniu równań w mechanice i chemii kwantowej (opisujących np. budowę atomów, oscylacje i rotacje cząsteczek) parametry numerujące kolejne dopuszczalne fizycznie rozwiązania. Liczby kwantowe przyjmują zwykle wartości całkowite, z pewnego określonego przedziału.
Przykładowo rozwiązując równanie Schrödingera dla atomu wodoru uzyskuje się trójparametrową rodzinę rozwiązań - tzw. funkcji falowych, opisujących (bez uwzględnienia spinu) możliwe zachowanie się elektronu w tym atomie - gdzie kolejne wartości trójek liczb kwantowych, czyli parametrów rozwiązań, odpowiadają poszczególnym stanom kwantowym, w jakich może znajdować się atom.
POSTULATY BOHRA -1(w atomie istnieją stacjonarne tory (orbity), po których elektron może krążyć bez wypromieniowywania energii. moment pędu na tej orbicie jest całkowitą wielokrotnością stałej plancka ∫pdq=nh. 2(elektron na n-tej orbicie stacjonarnj ma określoną wartość energii EN.wzbudzenia atomu wiąże się z promieniowaniem elektronu na orbitę wyższą ,położoną dalej od jądra, a więc odpowiadającą więkrzej energii.mvr=nh(kreślne) 3(emisja promieniowania wiąze się z przeskokiem elektronu z orbity wyższej na niższą. Towarzysząca temu przeskokowi zmiana energii atomu EK-EP=hυ.na podstawie tych postulatów możemy obliczyć promień orbity a także można wyznaczyc widmo atomu promieniującego somerfeld wprowadził do modelu atomu orbity eliptyczne .jedna z liczb kwantowych będzie się wiązała z energią elektronu na orbicie , druga z kształtem orbity i z momentem pędu na orbićie. Pierwsza główna liczba kwantowa n=1,2,3,...nieskończon. drugaliczba kwantowa poboczna l=0,1,2..(n-1).energia elektronu na torze zalerzy od kształtu elipsy widć to ze wzoru somerfelda na energię elektronu na orbicie n w atomie wodorupoczątkowo moment pędu elektronu na orbicie wyrażano wzorem: w tym ujęciu liczba l przedstawia moment pędu na orbicie wyrażony w jednostkach h/2Πcałkowity moment pędu spełnia równanie obrót elektronu dokoła własnej osi wywołuje własny nie orbitalny moment pędu zwany spinem elektron. Spin jest skwantowany.
Dwójłomność, zjawisko anizotropii optycznej kryształów odkryte w 1669 przez Duńczyka E. Bartholina. W kryształach wykazujących zjawisko dwójłomności (np. szpat islandzki, kwarc, cyrkon, lód, beryl itd.) światło załamując się, rozszczepia się na dwa promienie: zwyczajny i nadzwyczajny.
Promień zwyczajny znajduje się w płaszczyźnie padania światła i spełnia zwykłe prawo załamania (dla współczynnika załamania światła nz), natomiast promień nadzwyczajny odchylony jest na ogół od tej płaszczyzny i opisuje go współczynnik załamania zależny od kąta padania (n').
Istnieje wyróżniony co najmniej jeden kierunek kryształu. Jego oś optyczna. Jeśli światło biegnie równolegle do niej, oba promienie pokrywają się i nz=n'. Jeśli promień nadzwyczajny jest prostopadły do osi optycznej, jego współczynnik załamania różni się maksymalnie od nz, osiągając wartość oznaczoną nn.
Jeśli nn-nz<0, to kryształ nazywa się optycznie ujemnym, a przy nn>nz - optycznie dodatnim. Kryształy o wyróżnionej jednej osi optycznej nazywa się jednoosiowymi. Są też kryształy dwuosiowe. Promienie zwyczajny i nadzwyczajny są spolaryzowane liniowo w kierunkach prostopadłych do siebie.
Faradaya zjawisko, skręcanie płaszczyzny światła spolaryzowanego przez substancje optycznie nieaktywne, po umieszczeniu ich w polu magnetycznym o liniach sił równoległych do kierunku przechodzącej wiązki świetlnej.
Kąt skręcenia wynosi F = VBd, gdzie: V - stała charakterystyczna dla danej substancji, B - wartość indukcji pola magnetycznego, d - grubość warstwy substancji, przez którą przechodzi wiązka światła. Magnetyczna skręcalność molowa (zdefiniowana jako [F]M = (F M)/(ρBd), gdzie: M - masa molowa danej substancji, ρ - gęstość tej substancji) jest wielkością addytywną i służy do badań strukturalnych.
Clapeyrona równanie, równanie gazu doskonałego określające związek między jego temperaturą, ciśnieniem i objętością:
PV = nRT,
gdzie P- ciśnienie, V - objętość, n - liczba moli gazu, T - temperatura, R - stała gazowa (R = Nk, N - liczba Avogadro, k - stała Boltzmanna).
Z równania Clapeyrona wynikają prawa Boyle'a-Mariotte'a, Gay-Lussaca , Charlesa). Równanie to opisuje również z dobrym przybliżeniem rozrzedzone gazy rzeczywiste.
Przyspieszenie kątowe, , wielkość pseudowektorowa charakteryzująca zmiany prędkości kątowej bryły sztywnej lub punktu materialnego.
Przyspieszenie kątowe określone jest równaniem:
przy czym jest równoległe do przy przyspieszaniu ruchu obrotowego lub antyrównoległe do przy zwalnianiu. Jednostką przyspieszenia kątowego w układzie SI jest radian/s2.
Termodynamiki zasady, podstawowe prawa przyrody rządzące procesami zachodzącymi w układach termodynamicznych:
Zerowa zasada termodynamiki.
Jeżeli dwa ciała znajdują się w równowadze cieplnej z trzecim ciałem, to są też w równowadze cieplnej ze sobą - równowaga termodynamiczna AB, BC oznacza to, że AC przy identycznej temperaturze, ciśnieniu i reakcji chemicznej.
Energia wewnętrzna jest to energia, która może być:
-energią cieplną(ruch chaotyczny)
-energią potencjalną (ruch oddziaływania cząstek)
-energią kinetyczną i potencjalną (ruch oddziaływania cząstek)
-energią kinetyczną i potencjalną (ruchu drgającego w ciałach stałych)
Pierwsza zasada termodynamiki - przemiany gazowe
Pierwsza zasada termodynamiki to po prostu inna wersja zasady zachowania energii
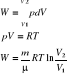
Ciepło pobrane przez układ musi być równe wzrostowi energii wewnętrznej układu plus pracy wykonywanej przez układ nad otoczeniem zewnętrznym
-przemiana izotermiczna
-przemiana adiabatyczna dQ=0 - bez wymiany ciepła
Nie można przekazać ciepła ciału o temp niższej ciału o temp wyższej.
1) pierwsza zasada termodynamiki - zmiana energii wewnętrznej układu równa jest różnicy ciepła dostarczonego do układu i pracy wykonanej przez ten układ. Zasada ta, równoważna zasadzie zachowania energii, w zarysach sformułowana została w 1842 przez J.R. Mayera, uściślona zaś w 1847 przez H.L.F. de Helmholtza.
2) druga zasada termodynamiki - istnieje entropia będąca funkcją stanu układu, stałą w odwracalnych procesach adiabatycznych i rosnącą we wszystkich innuch. Zasadę tę, zgodnie z którą kierunek wzrostu entropii może służyć do formalnego wyróżnienia kierunku upływu czasu (wszystkie inne prawa fizyki klasycznej nie ulegają zmianie przy zamianie przyszłości z przeszłością), podał w 1850 R.J.E. Clausius, a uściślił w 1851 Kelvin lord of Largs.
3) trzecia zasada termodynamiki - entropia układu o ustalonych parametrach (np. o stałym ciśnieniu lub objętości) i temperaturze zmierzającej do zera bezwzględnego zmierza również do zera. Zasadę tę, pozwalającą obliczyć bezwzględną wartość entropii (określanej przedtem tylko z dokładnością do stałej), podał w 1906 W.H. Nernst (tzw. twierdzenie Nernsta).
Niekiedy nazwą czwartej zasady termodynamiki określa się twierdzenie Onsagera, a za zasadę tzw. zerową uznaje się twierdzenie głoszące, że dwa ciała będące w równowadze termodynamicznej z pewnym układem są w równowadze termodynamicznej ze sobą.
Lorentza siła, siła działająca w polu elektromagnetycznym na poruszającą się cząstkę o ładunku e, z prędkością v, opisuje ją wzór: F=eE+(e/c)(vB), gdzie E - wektor natężenia pola elektrycznego, B - wektor indukcji pola magnetycznego (indukcja), c - prędkość światła, symbol "" oznacza iloczyn wektorowy (wszystkie wielkości zmierzone w jednym układzie odniesienia).
Zgodnie z powyższym wzorem przy nieobecności pola elektrycznego (E=0) siła działająca na cząstkę w samym polu magnetycznym jest zawsze prostopadła do kierunku ruchu cząstki, co powoduje, że w jednorodnym polu magnetycznym nierównoległym do kierunku ruchu cząstki porusza się ona po torze spiralnym, a jeśli składowa prędkości początkowej cząstki w kierunku równoległym do kierunku pola magnetycznego jest równa zero, wówczas tor cząstki jest kolisty, co wykorzystuje się w cyklotronach.
Boltzmanna rozkład, najbardziej prawdopodobny rozkład energetyczny cząstek izolowanego układu o stałej energii, zbudowanego z N nie oddziaływających, poza momentami zderzeń, cząstek podległych prawom fizyki klasycznej, dany wzorem:
ni= exp(+i),
gdzie: ni - średnia liczba cząstek w stanie o energii i, =k-1, k - stała Boltzmanna, - czynnik normalizacyjny.
Można wykazać, że
= ln(N/V)+3/2ln(h2/mkT),
gdzie: V - objętość układu, h stała Plancka, m - masa cząstki, T - temperatura układu. Rozkład ten opisuje klasyczny gaz idealny zbudowany z jednoatomowych cząsteczek.
Balmera seria, seria linii widmowych atomu wodoru, dla których długość fali daje się przedstawić w postaci (tzw. wzór Balmera, 1885)
= n2/(n2-4),
gdzie n=3,4,5,6..., = 364,57 nm. Uzasadnienie teoretyczne obserwowanej regularności daje mechanika kwantowa.
Nazwa pochodzi od nazwiska odkrywcy, fizyka szwajcarskiego, J.J. Balmera (1825-1898).
Rentgenowskie promieniowanie, promieniowanie X, rodzaj promieniowania elektromagnetycznego (fale elektromagnetyczne) o długości fali zawartej w przedziale od 0,1 pm do ok. 50 nm, tj. pomiędzy promieniowaniem gamma i ultrafioletowym, przy czym zakres promieniowania rentgenowskiego pokrywa się częściowo z niskoenergetycznym (tzw. miękkim) promieniowaniem gamma - rozróżnienie wynika z mechanizmu wytwarzania promieniowania: promieniowanie rentgenowskie powstaje przy przejściach elektronów na wewnętrzne powłoki elektronowe atomu, natomiast promieniowanie gamma w przemianach energetycznych zachodzących w jądrze atomowym.
Promieniowanie rentgenowskie może mieć zarówno widmo liniowe (promieniowanie charakterystyczne, Moseleya prawo, przy czym energia niesiona przez kwant charakterystycznego promieniowania X wyraża się wzorem hEi-Ef, gdzie: h - stała Plancka, Ei, Ef, - odpowiednio energia stanu początkowego i końcowego elektronu w atomie), jak i widmo ciągłe (powstające jako promieniowanie hamowania w procesie oddziaływania cząstki naładowanej z materią, lampa rentgenowska).
Promieniowanie rentgenowskie wykorzystuje się w badaniach strukturalnych (rentgenowska analiza strukturalna, Braggów-Wulfa warunek, lauegram) oraz do badania pierwiastkowego składu chemicznego (rentgenowska analiza widmowa). Ponadto promieniowanie rentgenowskie szeroko stosuje się w diagnostyce medycznej. Promieniowanie rentgenowskie odkrył w 1895 W.C. Roentgen.
Dulonga-Petita reguła (prawo), fenomenologiczna reguła fizykochemiczna mówiąca, że atomowe ciepło właściwe ciał stałych w stałej objętości jest wielkością stałą i wynosi 6 cal (deg mol)-1.
Prawo Dulonga-Petita spełnione jest z dobrą zgodnością przez większość pierwiastków i prostych związków w umiarkowanym zakresie temperatury, odstępstwa pogłębiają się w miarę obniżania temperatury.
Alfa cząstka, - jądro atomu 4He emitowane przez niektóre substancje promieniotwórcze w trakcie rozpadu alfa. Cząsteczki alfa produkowane są również w wielu reakcjach jądrowych. Cząsteczka alfa zbudowana jest z 2 protonów i 2 neutronów, ma więc ładunek elektryczny równy +2 ładunku elementarnego. Spin cząsteczki alfa wynosi 0, a masa 4,0027 j.m.a..
Beta rozpad, rozpad jądra promieniotwórczego, w wyniku którego z jądra emitowany jest (rozpad beta minus) elektron (negaton) i antyneutrino elektronowe lub (rozpad beta plus) pozyton i neutrino elektronowe.
W pierwszym przypadku liczba atomowa Z nowo powstałego jądra jest większa o jeden od Z jądra macierzystego, w drugim - zmniejsza się o jeden. Liczba masowa jądra A nie ulega zmianie w rozpadzie beta. Odkryto też odwrotny rozpad beta, tzn. reakcję zmiany Z jądra wywołaną oddziaływaniem neutrina (lub antyneutrina) z emisją cząstki beta jako produktu reakcji.
Rozpad obserwuje się również dla cząstek elementarnych, np. rozpad neutronu na proton, elektron i antyneutrino elektronowe. Ze względu na emisję dwóch ciał (cząstka beta i neutrino) z jądra w rozpadzie beta obserwuje się ciągłe widmo energii emitowanych cząstek beta.
Widmo promieniowania gamma pierwiastków promieniotwórczych ma charakter dyskretny, tj. obserwuje się oddzielne linie widmowe, energia odpowiadająca tym liniom pozwala indentyfikować promieniującą substancję.
Rozpad promieniotwórczy, zjawisko spontanicznej przemiany jądra atomowego danego izotopu w inne jądro. Podstawową własnością rozpadu promieniotwórczego jest brak wpływu fizykochemicznych czynników zewnętrznych na proces.
Ze względu na rodzaj przemiany zachodzącej w jądrze i towarzyszące mu zjawiska wyróżnia się: rozpad alfa, rozpady beta (beta plus lub beta minus), wychwyt elektronu, rozszczepienie jądra atomowego i inne, np. rozpad protonowy, hipotetyczny rozpad podwójny beta itp.
Ogólne zasady rozpadu promieniotwórczego odnoszą się również do przejść izomerycznych (izomeria jądrowa) zachodzących bez przekształcenia się jądra w jądro innego izotopu. Niezależnie od rodzaju procesu fizycznego prowadzącego do rozpadu promieniotwórczego zjawisko podlega prawu rozpadu promieniotwórczego.
Rozpadu promieniotwórczego prawo, prawo określające zmianę w czasie ilości jąder substancji promieniotwórczej na skutek rozpadu promieniotwórczego.
Określa je równanie różniczkowe postaci:
-dN(t)/dt = N(t),
gdzie: N(t) - chwilowa liczba jąder danego izotopu promieniotwórczego, - stała rozpadu.
Lewą stronę tego równania nazywa się aktywnością (aktywność źródła promieniotwóczego), znak minus wynika z ujemnej wartości pochodnej dN/dt. Jako prawo rozpadu promieniotwórczego traktuje się często wymiennie rozwiązanie przytoczonego równania postaci:
N(t) = No{exp(-t)} = No{exp[-(ln2)t/T1/2]},
gdzie: No - początkowa liczba jąder danego izotopu, T1/2 - czas połowicznego zaniku danego izotopu.
Bardziej złożone wyrażenia opisują rozpady sekwencyjne (równowaga promieniotwórcza).
Cyklotron, akcelerator cykliczny, w którym stosunkowo ciężkie cząstki (protony, jądra, jony) przyspieszane są polem elektrostatycznym o napięciu rzędu 100 kV i wysokiej częstości, istniejącym pomiędzy dwoma duantami, czyli płaskimi wydrążonymi półwalcami.
Cząstki poruszają się po torach spiralnych dzięki istnieniu stałego silnego pola magnetycznego prostopadłego do płaszczyzny przyspieszania.
Zasada działania oparta jest na obserwacji, że przy pominięciu efektów relatywistycznych (tj. wzrostu masy przyspieszanych cząstek) częstotliwość obiegu cząstek naładowanych po torze kołowym k (częstość cyklotronowa) nie zależy od ich energii, co pozwala łatwo zsynchronizować częstość obiegu cząstek z częstością zmian pola elektrycznego e, tak, że
k = e = (e/m)/( H/c),
gdzie e - ładunek przyspieszanej cząstki, m - jej masa, H - wartość bezwzględna wektora natężenia pola magnetycznego, c-prędkość światła.
Cyklotron był najwcześniejszym akceleratorem cyklicznym, pierwszy został skonstruowany przez E. Lawrence'a i M. Livingstone'a w Kalifornii w 1931.
Ograniczeniem energii osiąganych za pomocą cyklotronu są efekty relatywistyczne wpływające na opóźnianie się cząstek o dużych energiach względem zmian pola, co doprowadza do utraty efektywności przyspieszania. Częściowo można temu zaradzić, zwiększając pole magnetyczne wraz z promieniem, co prowadzi do konstrukcji nazywanej cyklotronem izochronicznym.
W Polsce pierwszy cyklotron uruchomiony został w latach powojennych na Uniwersytecie Jagiellońskim, następnie został przeniesiony do Instytutu Fizyki Jądrowej (IFJ, również w Krakowie), gdzie był modernizowany i pracował do początku lat 90., osiągając energię protonów równą 3 MeV. Od lat 60. w IFJ pracuje większy cyklotron, pozwalający osiągać dwukrotnie wyższe energie protonów i przyspieszać cząstki alfa do energii 29 MeV.
W obecnej chwili w Polsce kończy się budowę dwóch dalszych cyklotronów: ciężkich jonów w Warszawie i izochronicznego w Krakowie.
Reaktor jądrowy, reaktor atomowy, stos atomowy, urządzenie służące do wytwarzania kontrolowanej reakcji łańcuchowej, tj. ciągłego pozyskiwania energii z rozszczepiania jąder atomowych.
Stan kontrolowanej reakcji jądrowej podtrzymującej się samoczynnie na ustalonym poziomie nazywany jest stanem krytycznym. Jeśli intensywność reakcji narasta, to stan jest nadkrytyczny, gdy wygasa, to stan jest podkrytyczny.
Stan krytyczny uzyskuje się, gdy efektywny współczynnik mnożenia neutronów = 1, tzn. gdy strumień neutronów pochodzących z rozszczepienia jąder atomowych kompensuje straty neutronów wynikające z ich rozproszenia i pochłonięcia. Odchylenie stanu reaktora jądrowego od stanu krytycznego opisuje tzw. reaktywność ρ = (-1)/
Reaktor jest sterowalny i bezpieczny, gdy ma małą, dodatnią reaktywność związaną z neutronami opóźnionymi. Typowy reaktor jądrowy zbudowany jest z rdzenia, reflektora neutronów oraz osłon biologicznych. Sam rdzeń zawiera pręty paliwowe, pręty regulacyjne, pręty bezpieczeństwa, moderator, kanały chłodzenia i kanały badawcze.
Podstawowym elementem reaktora jądrowego są pręty paliwowe, które zawierają paliwo jądrowe w formie fizykochemicznej i o stopniu wzbogacenia dostosowanym do konstrukcji reaktora jądrowego. Moderator wykonany jest z materiałów zawierających duże ilości atomów o małej liczbie porządkowej Z, skutecznie zmniejszających energię neutronów produkowanych w trakcie rozszczepiania.
Pręty regulujące i pręty bezpieczeństwa zbudowane są z substancji pochłaniających neutrony (np. bor, kadm), przy czym pręty regulacyjne służą do precyzyjnej zmiany strumienia neutronów, podczas gdy pręty bezpieczeństwa mają za zadanie całkowite przerwanie reakcji łańcuchowej w sytuacji awaryjnej - oba te rodzaje prętów wsuwa się i wysuwa z rdzenia w miarę potrzeby.
Przez kanały chłodzące przepompowywuje się chłodziwo tzw. pierwszego obiegu (typowym chłodziwem jest woda, stosuje się również powietrze, azot, ciekły sód itd.). Kanały badawcze służą do kontrolowania poziomu strumienia neutronów, wykonywania naświetlań itp.
! Schemat reaktora jądrowego
Ze względu na zastosowanie rozróżnia się:
1) reaktory jądrowe badawcze (o małej, tzw. zerowej mocy, wykorzystywane w badaniach naukowych jako silne źródła neutronów),
2) reaktory jądrowe produkcyjne (służące do wytwarzania sztucznych pierwiastków promieniotwórczych na drodze aktywacji, głównie do produkcji plutonu - szczególną klasę tych reaktorów stanowią tzw. reaktory jądrowe powielające, w których paliwo jądrowe w trakcie wypalania przekształca się w inny rodzaj paliwa jądrowego),
3) reaktory jądrowe energetyczne (wytwarzające energię cieplną przekształcaną w energię mechaniczną w napędach nuklearnych okrętów lub w energię elektryczną w energetyce jądrowej),
4) reaktory jądrowe doświadczalne (prototypy nowych rozwiązań technicznych stosowanych w reaktorach jądrowych).
Częstym kryterium klasyfikacji reaktorów jądrowych jest rodzaj zastosowanego moderatora i chłodziwa - istnieją zatem reaktory jądrowe wodno-wodne, ciężkowodno-wodne (ciężka woda), grafitowo-wodne, grafitowo-powietrzne, grafitowo-sodowe itp.
Innym rodzajem klasyfikacji reaktorów jądrowych jest podział ze względu na wykorzystywaną energię neutronów lub wielkość ich strumienia (cechy te określają rodzaj paliwa i wiele innych parametrów reaktora). Zgodnie z tym kryterium rozróżnia się:
1) reaktory jądrowe wysokostrumieniowe (o strumieniu neutronów przekraczającym 1014 cząstek/cm2s),
2) reaktory jądrowe prędkie (gdy reakcja rozszczepienia zachodzi dzięki neutronom prędkim),
3) reaktory jądrowe pośrednie (gdy stosuje się neutrony pośrednie),
4) reaktory jądrowe termiczne (wykorzystywane są neutrony termiczne),
5) reaktory jądrowe epitermiczne (reakcja zachodzi dzięki neutronom epitermicznym).
Pierwszy reaktor jądrowy zbudowano w ramach Manhattan Project (CP-1, E. Fermi), obecnie na świecie eksploatowanych jest ich kilka tysięcy, w większości są one reaktorami badawczymi. W Polsce istnieją trzy badawcze reaktory jądrowe, wszystkie w Świerku (noszą nazwy Ewa, Maria i Agata).
Powłoki elektronowe, powierzchnie dozwolonej energii elektronów w atomie (poziomy energetyczne).
W wyniku wzajemnych oddziaływań momentów magnetycznych orbitalnych, spinowych i jądrowego powłoki elektronowe rozwarstwiają się na podpowłoki elektronowe (subtelna struktura, nadsubtelna struktura). W nawiązaniu do modelu atomu Bohra kolejne powłoki elektronowe określa się literami K, L, M, itd.
Heisenberga zasada nieoznaczoności, fundamentalna zasada fizyki kwantowej mówiąca o tym, że iloczyn niepewności jednoczesnego poznania pewnych wielkości (zwanych kanonicznie sprzężonymi w sensie formalizmu hamiltonowskiego: np. chwilowych wartości pędu p i położenia x, energii E i czasu jej pomiaru t, współrzędnej kątowej leżącej w płaszczyźnie xy i składowej Jz krętu, itd.) nie może być mniejszy od stałej Plancka h podzielonej przez podwojoną liczbę :, (h=h/2).
Mała wartość liczbowa stałej Plancka powoduje, że zasada nieoznaczoności jest istotna
Konsekwencją zachowania parzystości kombinowanej CPT jest symetria cząstek i antycząstek, tj. równość ich mas, czasów życia, spinów i in. parametrów dynamicznych oraz bezwzględnej wartości ładunków elektrycznych i momentów magnetycznych.
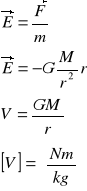
Wyszukiwarka
Podobne podstrony:
strony energetyczne, Wykłady i ćwiczenia
notatki wykłady ćwiczenia
El en i środowisko 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
Ćwiczenia semestr VI, Lekarski GUMed, III rok, INTERNA, PLAN WYKŁADÓW I ĆWICZEŃ 2011
3-7.12.09, Studia, IV rok, IV rok, VII semestr, Waloryzacja przyrodnicza, wyklady cwiczenia w word
Narazenia od pól elektromagnetycznych 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład
Statyka - Przestrzenny Układ Sił, sem II, Mechanika Techniczna I - Wykład.Ćwiczenia, Zestaw V (oce)
Ekonomia- wszystkie wykłady i ćwiczenia- ściaga, OGRODNICTWO UP LUBLIN, EKONOMIA
Narazenia od pól elektromagnetycznych 13 14 2, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład
Pedagogika - Notki z wykładów i ćwiczeń, Pedagogika
Pedagogika lecznicza2 wykład i ćwiczenia
Fizjologia i anatomia człowieka Krew (wykłady i ćwiczenia)
Moc bierna 13 14 1, Prywatne, EN-DI semestr 4, Elektroenergetyka, wykład + ćwiczenia
Wykład z ćwiczeń - 21.01.2011 (piątek) mgr A. Szczepanek, UJK.Fizjoterapia, - Notatki - Rok I -, Bio
więcej podobnych podstron