Laboratorium fizyka- Wyznaczanie ciepła topnienia lodu.

1. Wstęp teoretyczny:

- Topnienie jest przemianą fazową polegającą na przejściu ciała ze stanu stałego w stan ciekły, pod wpływem dostarczonego ciepła. Jeżeli będziemy ogrzewać ciało krystaliczne to najpierw zauważymy liniowy wzrost temperatury tj. rys. odcinek AB

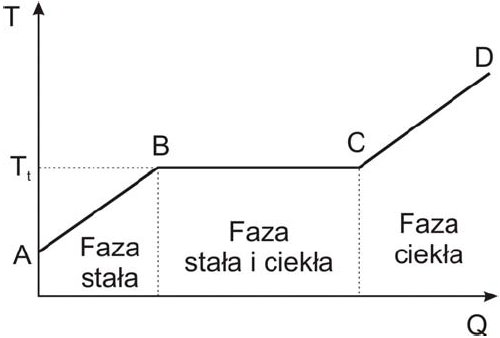
Rys.1 Zmiany temperatury w procesie topnienia ciała krystalicznego.

- po osiągnięciu temperatury przemiany fazowej T_t dalsze dostarczanie ciepła nie powoduje wzrostu temperatury ciała odcinek BC. Na tym odcinku ciepło dostarczone jest w całości zużyte na energię wiązania w cząsteczek w sieci krystalicznej. Są jeszcze obecne dwie fazy, woda i ciało stałe.

- w punkcie C ciało uległo w całości stopieniu

- dalsze dostarczanie ciepła powoduje wzrost temperatuty fazy ciekłej, odcinek CD

Punkt topnienia: jest to temperatura w której faza ciekła znajduje się w równowadze z fazą stałą.

ciepło właściwe - określa ilość ciepła, jaką należy doprowadzić, aby ogrzać substancję o jednostkowej masie o 1 stopień.

ciepło całkowite

Q­­₁- ciepło zużyte na ogrzanie ciała stałego od temperatury początkowej do temperatury topnienia.

Q₂- ciepło topnienia zużyte na zmianę stanu skupienia ciała

Q­₃- ciepło zużyte na ogrzanie powstałej cieczy

wzór na ciepło topnienia lodu

Do pomiaru ilości ciepła pobieranego np. podczas topienia lodu służy urządzenie zwane kalorymetrem. Jest ono zbudowane z zewnętrznego naczynia izolującego oraz wewnętrznego naczynia, w którym wykonujemy doświadczenie. Oba pojemniki są zamocowane w ten sposób, że pomiędzy nimi znajduje się izolująca warstwa powietrza, tak, że nie następuje wymiana ciepła między wewnętrznym a zewnętrznym naczyniem. W obliczeniach wykorzystujemy tylko wewnętrzną część kalorymetru która pochłania lub oddaje ciepło.

ciepło pobrane

ciepło oddane

Plan pracy:

1. Zapoznaję się z zestawem eksperymentalnym.

2. Sprawdzam prawidłowe ustawienia wagi.

3. Wyznaczam masę naczynia środkowego oraz mieszadełka.

4. Po napełnieniu kalorymetru ciepłą wodą (100-200ml) wyznaczam jego masę z wodą.

5. Odczytuję dokładną temperaturę początkową wody i kalorymetru.

6. Wyjmuję lód z naczynia (20-30g) (musi mieć 0ºC), dokładnie osuszam bibułą
   i wrzucam do kalorymetru.

7. Mieszam aż do całkowitego roztopienia się lodu.

8. Odczytuję temperaturę i wyznaczam masę kalorymetru z wodą.

Celem ćwiczenia było wyznaczenie ciepła topnienia lodu.

2. OPRACOWANIE WYNIKÓW:

Pomiary zebrano w tabeli, na ich podstawie obliczono masę lodu i masę wody które są potrzebne do obliczenia ciepła topnienia lodu.

Nr.	Początkowa masa kalorymetru (bez wody) mk [g]	Masa kalorymetru z wodą [g]	Początkowa temperatura wody w kalorymetrze Tp [^oC]	Temperatura końcowa wody po dodaniu lodu i jego roztopieniu Tk	Końcowa masa kalorymetru z wodą i roztopionym lodem [g]	Masa wody mw [g]	Masa lodu ml[g]
1	115,6	523,1	23	14,4	565,1	407,5	42
2	115,6	487,4	22,6	19,4	501,2	371,8	13,8
3	115,6	480,3	22,6	19,8	491,7	364,7	11,4
4	115,6	501,7	21,8	18,8	514,1	386,1	12,4
5	115,6	483,6	20,8	18,4	495,1	368	11,5
6	115,6	517,3	21	15,7	542,2	401,7	24,9

Dla każdego pomiaru obliczono ciepło topnienia lodu z wzoru:

Jako c_k­­- ciepło właściwe kalorymetru przyjęto ciepło właściwe aluminium

= 0,92[J/g*K] a za ciepło właściwe wody przyjęto c_w=4,187 [J/g*K]

Ad1.
310,8493 [J/g]

Analogicznie obliczono dalsze pomiary:

Ad2. q= 367,7934 [J/g]

Ad3. q= 401,1739 [J/g]

Ad4. q= 416,8434 [J/g]

Ad5. q= 343,7568 [J/g]

Ad6. q= 380,6358 [J/g]

Korzystając z wzoru na obliczenie niepewności za pomocą różniczki zupełnej obliczono niepewności pomiarów.

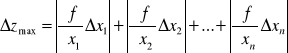
Najpierw obliczono ile wynoszą niepewności pomiarowe dla:

Δm_w, Δm_k, Δm_l, ΔT_p, ΔT_k i tak po kolei:

- Δm_w- masę wody wyznaczyliśmy ważąc najpierw pusty kalorymetr a później kalorymetr z wodą każde ważenie objęte było niedokładnością 0,1 więc ostateczna niedokładność masy wody wynosi= 0,2 [g].

- Δm_k- masę kalorymetru wyznaczono poprzez jego zważenie więc niedokładność masy kalorymetru równa się niedokładności wagi = 0,1[g]

- Δm_l- masę lodu wyznaczamy jako różnicę mas kalorymetru z wodą i roztopionym lodem a masą kalorymetru z wodą więc niepewności obu ważeń sumują się i ostatecznie niepewność masy lodu wynosi 0,2[g]

- ΔT_p, ΔT_k- obarczone są niepewnością termometru wynoszącą 0,2[^oC]

Przekształcamy wzór na pośrednią niepewność pomiarową i otrzymujemy 5 pochodnych cząstkowych:

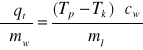
(1)

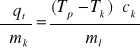
(2)

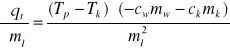
(3)

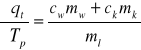
(4)

(5)

OSTATECZNA NIEPEWNOŚĆ POMIAROWA:

Obliczenia niepewności zebrano w tabeli:

Numer pomiaru	|(1)*∆mw|	|(2)*∆mk|	|(3)*∆ml|	|(4)* ∆Tp	|(5)*∆Tk|	q max
1	0,171468	0,018838	1,767343	8,631212	8,631212	19,22007
2	0,194180	0,021333	5,589006	24,10259	24,10259	54,00970
3	0,205677	0,022596	7,038139	28,65528	28,65528	64,57697
4	0,202597	0,022258	6,723281	27,78956	27,78956	62,52725
5	0,174762	0,019200	5,978379	28,64640	28,64640	63,46514
6	0,178242	0,019582	3,057315	14,36361	14,36361	31,98237

PODSUMOWANIE:

Porównując otrzymane wyniki z wartością tablicową ciepła topnienia lodu wynoszącą= 332 [J/g] oraz biorąc pod uwagę błędy poszczególnych pomiarów zauważamy że tylko 3 wartości nie mieszczą się w granicach błędu jest to pomiar 3, 4 i 5 jednak nieznacznie odbiegają od wartości teoretycznych. Patrząc w tabelę widać że im mniej lodu wrzuciliśmy tym większy był błąd pomiaru co dawało zafałszowane wyniki ostateczne. Mogło to być spowodowane niedokładnym osuszeniem lodu przez co zmniejszaliśmy ilość ciepła potrzebną do stopienia tego lodu. Najbliższą wartość tablicowej uzyskaliśmy w pomiarze pierwszym tam też masa lodu była największa co znacznie wpłynęło na niepewność obniżyło ją (warto zauważyć ze przy pochodnych masa lodu występuje w mianowniku wiec z jej wzrostem malała niepewność.

---