Laboratorium Podstaw Fizyki

Ćwiczenie 57C

Badanie efektu Halla

1. Cele ćwiczenia:

- Wyznaczenie charakterystyk hallotronu

- Wyznaczenie czułości hallotronu

- Wyznaczenie koncentracji elektronów swobodnych

- Wyznaczenie czułości kątowej układu

2. Wstęp

Jeżeli płytkę z metalu włączymy w obwód prądu stałego i umieścimy w polu magnetycznym , którego wektor indukcji B jest prostopadły do powierzchni płytki i do kierunku płynącego prądu elektrycznego , to między punktami A i B wytworzy się różnica potencjałów UH , zwana napięciem Halla , lub zjawiskiem galwanometrycznym ( RYS ).

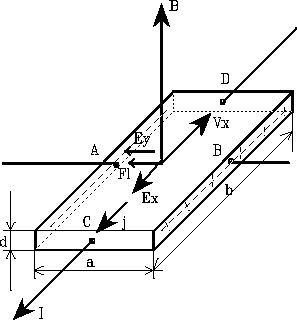
Załóżmy , że nośnikami prądu są elektrony. Jeżeli do punktów C i D przyłożymy napięcie , to w razie braku pola magnetycznego przez próbkę będzie płynąc prąd o natężeniu I. Wytworzone w próbce pole elektryczne o natężeniu Ex będzie skierowane zgodnie z kierunkiem płynącego prądu , natomiast elektrony poruszać się będą w kierunku przeciwnym polu z prędkością Vx. Gęstość prądu płynącego przez płytkę jest określona wzorem :

j = e n Vx.

Natężenie prądu I można określić jako iloczyn gęstości prądu j i powierzchni S prostopadłej do wektora gęstości prądu
, czyli : I = e n Vx a d.

W obecności pola magnetycznego o indukcji B , na elektrony poruszające się w tym polu z prędkością Vx , działa siła Lorentza :

.

Tak więc każdy elektron w płytce , poruszający się z prędkością Vx , zostaje odchylony od swego początkowego kierunku ruchu zgodnie z powyższym wzorem. Wskutek zmiany torów elektrony gromadzą się na jednej krawędzi płytki , natomiast na drugiej wytwarza się niedobór elektronów. Dzięki temu powstaje pole elektryczne o natężeniu :

Proces gromadzenia się ładunków trwa tak długo , aż powstałe pole poprzeczne Ey , działające na elektrony z siłą : Fy = - e Ey , zrównoważy siłę Lorentza , czyli Fy = FL.

Pamiętając , że wektory Vx oraz B są do siebie prostopadłe oraz korzystając z powyższych zależności , otrzymujemy wyrażenie określające napięcie Halla :

, w którym
.

Mierząc natężenie prądu I płynącego przez płytkę , napięcie Halla UH oraz znając współczynnik , można wyznaczyć indukcję magnetyczną B.

Urządzenie służące do wyznaczania indukcji magnetycznej nazywa się HALLOTRONEM , współczynnik zaś nazywamy czułością hallotronu. Zjawisku Halla towarzyszy wiele innych zjawisk fizycznych , które mogą wpływać na wartość mierzonego napięcia Halla. Jednym z nich jest zjawisko tzw. asymetrii pierwotnej , wiążące się z poprawnym wykonaniem elektrod hallowskich. Polega ono na tym , że gdy elektrody nie leżą dokładnie naprzeciwko siebie , tzn. nie leżą na tej samej powierzchni ekwipotencjalnej , wówczas gdy brak pola magnetycznego , lecz prąd I płynie przez hallotron , między elektrodami hallowskimi wytwarza się różnica potencjałów UA , zwana napięciem asymetrii pierwotnej , które sumuje się z napięciem Halla i utrudnia pomiar.

3. Przyrządy i układ pomiarowy:

Do dyspozycji mieliśmy następujące przyrządy:

• Hallotron

• Zasilacz hallotronu

• Miliamperomierz

• Woltomierz

Schemat układu pomiarowego:

4. Obliczenia

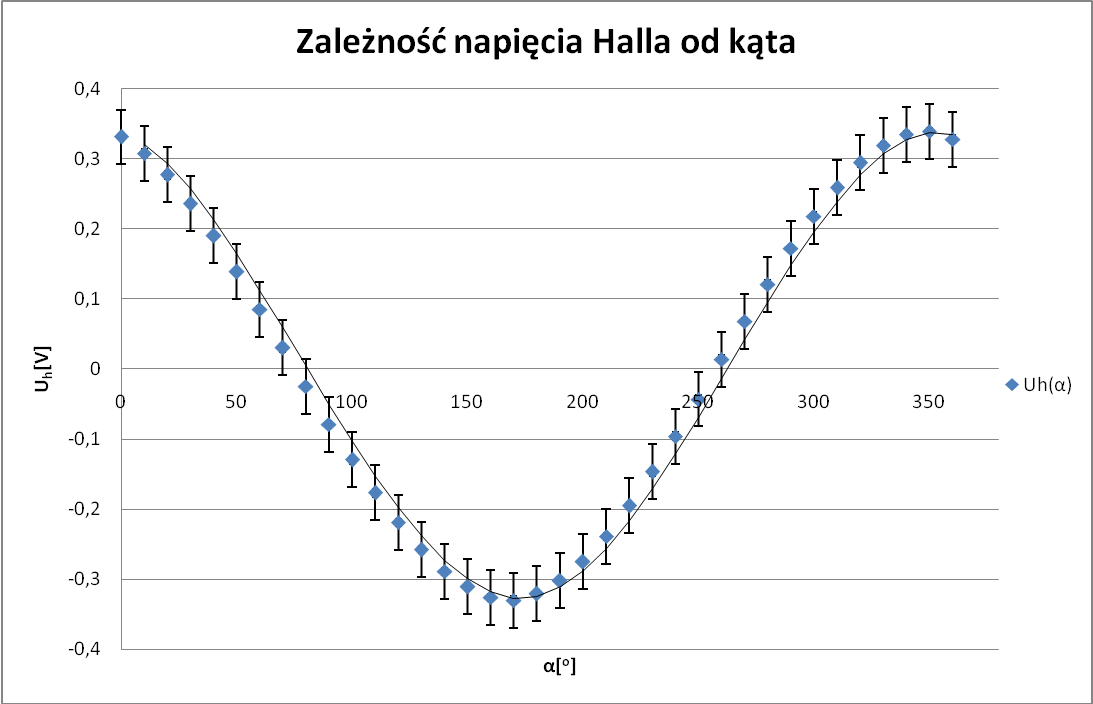
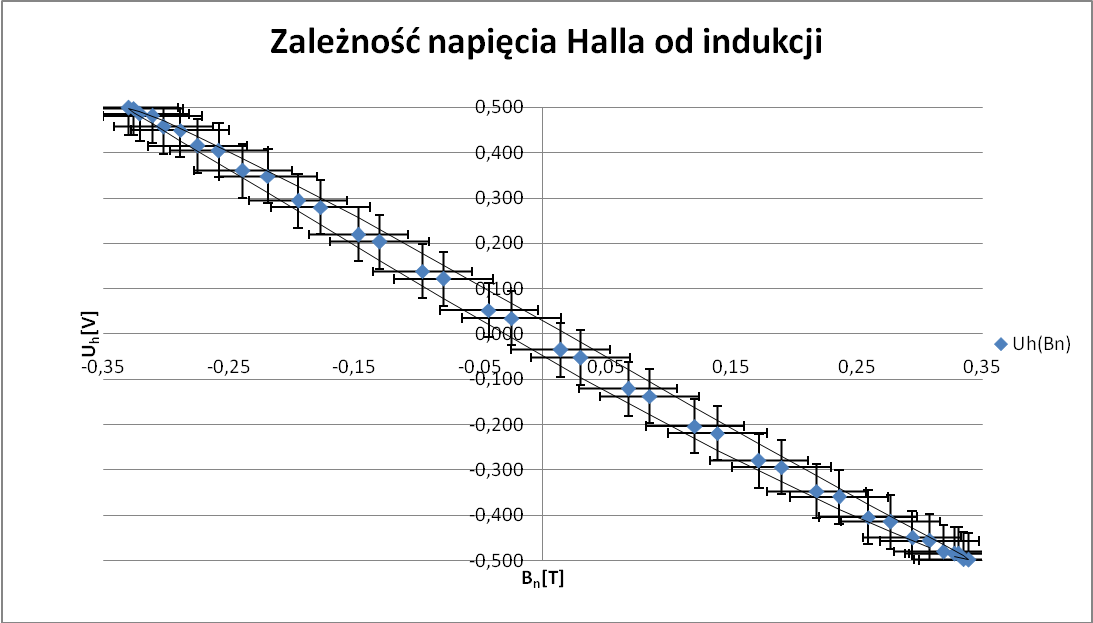
Is[mA]	ΔIs[mA]	α[^o]	Uh[V]	ΔUh[V]	Bn[T]
11	0,075	0	0,331	0,010	-0,485
11	0,075	10	0,308	0,010	-0,457
11	0,075	20	0,277	0,010	-0,415
11	0,075	30	0,236	0,010	-0,360
11	0,075	40	0,19	0,010	-0,294
11	0,075	50	0,139	0,010	-0,219
11	0,075	60	0,085	0,010	-0,138
11	0,075	70	0,03	0,010	-0,052
11	0,075	80	-0,025	0,010	0,035
11	0,075	90	-0,079	0,010	0,121
11	0,075	100	-0,13	0,010	0,203
11	0,075	110	-0,177	0,010	0,280
11	0,075	120	-0,219	0,010	0,347
11	0,075	130	-0,258	0,010	0,405
11	0,075	140	-0,289	0,010	0,449
11	0,075	150	-0,311	0,010	0,481
11	0,075	160	-0,326	0,010	0,497
11	0,075	170	-0,33	0,010	0,499
11	0,075	180	-0,321	0,010	0,485
11	0,075	190	-0,302	0,010	0,457
11	0,075	200	-0,275	0,010	0,415
11	0,075	210	-0,239	0,010	0,360
11	0,075	220	-0,195	0,010	0,294
11	0,075	230	-0,147	0,010	0,219
11	0,075	240	-0,096	0,010	0,138
11	0,075	250	-0,043	0,010	0,052
11	0,075	260	0,014	0,010	-0,035
11	0,075	270	0,068	0,010	-0,121
11	0,075	280	0,121	0,010	-0,203
11	0,075	290	0,172	0,010	-0,280
11	0,075	300	0,218	0,010	-0,347
11	0,075	310	0,259	0,010	-0,405
11	0,075	320	0,294	0,010	-0,449
11	0,075	330	0,319	0,010	-0,481
11	0,075	340	0,335	0,010	-0,497
11	0,075	350	0,339	0,010	-0,499
11	0,075	360	0,328	0,010	-0,485

1) Pomiary dla I_S=11mA

Wzory i dane wykorzystane w obliczeniach:

Przykładowe obliczenia:

Aby obliczyć
stosujemy wzór

, przykładowo dla 120
:

Identyczne obliczenia wykonałem dla pozostałych kątów.

Błąd pomiaru woltomierza:

Błąd pomiaru amperomierza:

2) Pomiary dla I_S=14mA

Is[mA]	ΔIs[mA]	α[^o]	Uh[V]	ΔUh[V]	Bn [T]
14	0,075	0	0,414	0,010	-0,485
14	0,075	10	0,386	0,010	-0,457
14	0,075	20	0,346	0,010	-0,415
14	0,075	30	0,297	0,010	-0,360
14	0,075	40	0,239	0,010	-0,294
14	0,075	50	0,173	0,010	-0,219
14	0,075	60	0,107	0,010	-0,138
14	0,075	70	0,039	0,010	-0,052
14	0,075	80	-0,032	0,010	0,035
14	0,075	90	-0,099	0,010	0,121
14	0,075	100	-0,163	0,010	0,203
14	0,075	110	-0,221	0,010	0,280
14	0,075	120	-0,275	0,010	0,347
14	0,075	130	-0,323	0,010	0,405
14	0,075	140	-0,361	0,010	0,449
14	0,075	150	-0,39	0,010	0,481
14	0,075	160	-0,408	0,010	0,497
14	0,075	170	-0,412	0,010	0,499
14	0,075	180	-0,401	0,010	0,485
14	0,075	190	-0,377	0,010	0,457
14	0,075	200	-0,341	0,010	0,415
14	0,075	210	-0,295	0,010	0,360
14	0,075	220	-0,242	0,010	0,294
14	0,075	230	-0,183	0,010	0,219
14	0,075	240	-0,117	0,010	0,138
14	0,075	250	-0,051	0,010	0,052
14	0,075	260	0,017	0,010	-0,035
14	0,075	270	0,088	0,010	-0,121
14	0,075	280	0,155	0,010	-0,203
14	0,075	290	0,218	0,010	-0,280
14	0,075	300	0,277	0,010	-0,347
14	0,075	310	0,327	0,010	-0,405
14	0,075	320	0,369	0,010	-0,449
14	0,075	330	0,402	0,010	-0,481
14	0,075	340	0,422	0,010	-0,497
14	0,075	350	0,425	0,010	-0,499
14	0,075	360	0,412	0,010	-0,485

Identyczne obliczenia jak dla I_S=11mA

Czułość hallotronu:

Czułość hallotronu wyznaczyłem przy pomocy programu umieszczonego na stronie http://www.if.pwr.wroc.pl/lpf/index.php?menu=pomoce . Dzięki niemu skorzystałem z regresji liniowej wykresu U_H i wyznaczyłem współczynnik a. Podstawiając do:

otrzymuję:

Błąd czułości hallotronu wyznaczam za pomocą metody różniczki zupełnej:

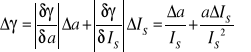
więc

Koncentracje elektronów obliczam według wzoru:

czyli

Błąd koncentracji elektronów wyznaczam stosując metodę różniczki zupełnej:

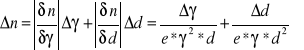
więc

3) Pomiary dla stałego kąta α=60 ^o

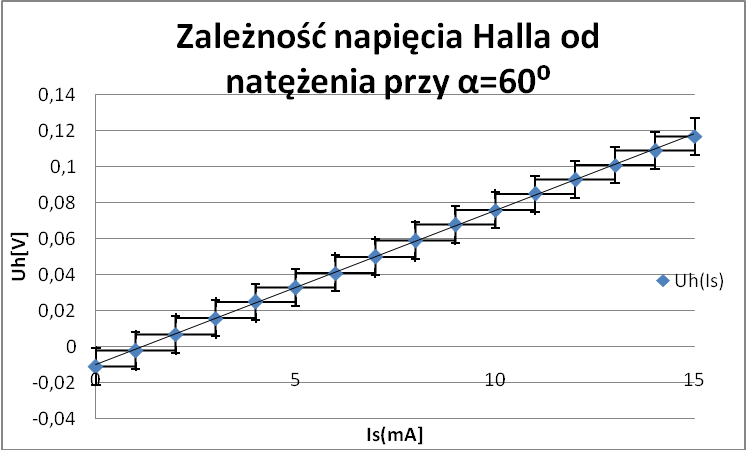
α[^o]	Is[mA]	Uh[V]
60	0	-0,011
60	1	-0,002
60	2	0,007
60	3	0,016
60	4	0,025
60	5	0,033
60	6	0,041
60	7	0,05
60	8	0,059
60	9	0,068
60	10	0,076
60	11	0,085
60	12	0,093
60	13	0,101
60	14	0,109
60	15	0,117

Czułość hallotronu:

Korzystałem z tego samego programu.

czyli

Błąd czułości Hallotronu obliczam metodą różniczki zupełnej:

więc

Koncentracje elektronów obliczam ze wzoru:

czyli

Błąd bezwzględny wyznaczam za pomocą metody różniczki zupełnej:

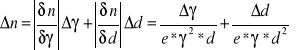
czyli

5. Wnioski

Czułości hallotronu, przy stałym i zmiennym natężeniu, są porównywalne. Błędy względne czułości hallotronu i koncentracji elektronu mieszczą się w granicach normy. Na precyzyjność pomiarów mogły wpłynąć błędy urządzeń pomiarowych oraz błędy ludzkie.

---