METODY PRZESTRZENI STANÓW

Sposoby przejścia między różnymi opisami

Opis obiektu w przestrzeni stanów nie jest jednoznaczny, tj. różne zestawy macierzy A, b, c mogą opisywać obiekt o tych samych własnościach. Powstaje pytanie jak wybrać wektor stanu mając opis obiektu w postaci transmitancji. Istnieje kilka standardowych sposobów przejścia, które pozwalają na uzyskanie tzw. kanonicznych postaci macierzy A, b, c (metoda bezpośrednia, równoległa, iteracyjna). Weźmy obiekt opisany transmitancją :

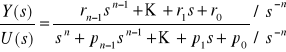
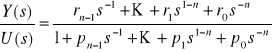
, gdzie

, czyli

.

Rysujemy schemat blokowy wewnętrznej struktury obiektu pamiętając, że mnożenie przez s^-1 oznacza całkowanie.

r_n-1

r_n-2

...... ....

U(s) E(s) Y(s)

∫ ∫ ... ∫ r₀

x_n x_n-1 x₂ x₁

-p_n-1

-p_n-2

.... . . . . .

-p₀

Na poszczególne zmienne stanu x_i (t) wybieramy wielkości :

Po przejściu do dziedziny czasu otrzymuje się układ równań różniczkowych :

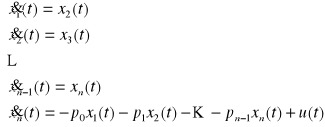
równanie wyjścia :

Wykorzystując zapis macierzowy :

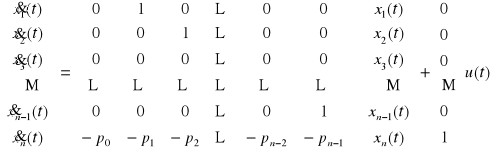
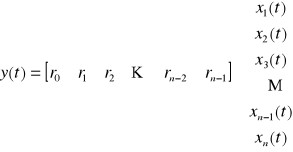
W ten sposób otrzymaliśmy jedną z postaci kanonicznych Brunowsky'ego - Luenbergera macierzy A, b, c. Jest to tzw. postać kanoniczna dla sterowania. Stosując inny tok postępowania można otrzymać tzw. postać kanoniczną dla obserwowania.

;

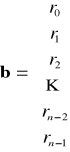
Przejście odwrotne, tzn. z opisu przestrzeni stanów do transmitancji wykonuje się następująco :

Przejście pomiędzy równaniem różniczkowym a transmitancją wykonuje się za pomocą przekształcenia Laplace'a.

Sterowalność i obserwowalność

W przypadku opisu wektorem stanu, może zdarzyć się tak, że przy dostępnym sterowaniu nie jesteśmy w stanie wpływać na niektóre zmienne. Mówimy wtedy, że te zmienne nie są sterowalne. Analogicznie niektóre zmienne stanu mogą w ogóle nie wpływać na wyjście. Mówimy wtedy, że te zmienne nie są obserwowalne. Ogólnie zmienne stanu można podzielić na cztery kategorie.

x - zmienne stanu

sterowalne

i obserwowalne

niesterowalne y(t)

i obserwowalne

u(t) sterowalne

i nieobserwowalne

niesterowalne

i nieobserwowalne

Pojęcie sterowalności i obserwowalności prześledźmy na przykładzie obiektu jakim jest myślowy model zegara wskazówkowego. Wielkości wejściowe są wprowadzane do obiektu za pomocą pokręteł umieszczonych z tyłu. Wielkościami wyjściowymi jest położenie wskazówek na cyferblacie. Cały mechanizm zegara przetwarza położenie pokręteł na położenie wskazówek. Zmiennymi stanu są sprężyny znajdujące się wewnątrz zegara. Zmienne stanu reprezentują zmagazynowaną w obiekcie energię. Kółka zębate są członami proporcjonalnymi i stanowią fizyczne połączenie pomiędzy wejściem, zmiennymi stanu i wyjściem. Można je interpretować jako współczynniki macierzy. Zmienne stanu są sterowalne, jeżeli kręcąc pokrętłami mamy wpływ na daną sprężynę. Zmienne stanu są obserwowalne, gdy stan danej sprężyny ma wpływ na położenie wskazówek. Sterowalność i obserwowalność zależy od wewnętrznych połączeń w strukturze obiektu. Dla obiektów liniowych wykryto [Kalman] odpowiedni warunek matematyczny, pozwalający testować wewnętrzną strukturę obiektu.

Twierdzenia o sterowalności i obserwowalności

Układ liniowy stacjonarny o jednym wejściu jest sterowalny wtedy i tylko wtedy, gdy rząd macierzy sterowalności Q jest pełny, gdzie

,

czyli rz Q = n.

W praktyce sprawdza się warunek : czy det Q ≠ 0.

Układ liniowy stacjonarny o jednym wyjściu jest obserwowalny wtedy i tylko wtedy, gdy rząd macierzy obserwowalności N jest pełny.

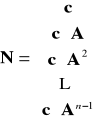
, czyli rz N = n.

W praktyce sprawdza się warunek det N ≠ 0.

Obiekt zapisany w postaci kanonicznej do sterowania jest w pełni sterowalny. Obiekt zapisany w postaci kanonicznej do obserwowania jest w pełni obserwowalny.

Liniowa transformacja wektora stanu.

Obiekt jest opisany przy pomocy następujących równań stanu :

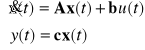
Chcemy by obiekt był opisany przy pomocy innego wektora stanu, zdefiniowanego w sposób następujący :

gdzie T - macierz transformacji, spełniająca następujące warunki :

dim T = n, co oznacza, że wektory x i v mają ten sam wymiar,

rz T = n ⇔ det T ≠ 0 - macierz jest nieosobliwa

W nowych współrzędnych obiekt jest opisany równaniami :

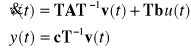
Transformacja T wektora stanu działa w sposób następujący na trójkę macierzy A, b, c.

Opis za pomocą wektora stanu nie jest jednoznaczny. Dwa obiekty mają taką samą dynamikę wtedy i tylko wtedy, gdy ich równania charakterystyczne maję te same pierwiastki. Liniowa transformacja wektora stanu nie zmienia położenia pierwiastków równania charakterystycznego.

---