Politechnika Śląska w Gliwicach

Katedra Mechaniki Robotów i Maszyn

SPRAWOZDANIE Z TMM

TEMAT: doświadczalne WYZNACZANIE JEDNEJ ZE SKŁADOWYCH TENSORA BEZWŁADNOŚCI.

Prowadzący ćwiczenie: dr inż. Tadeusz Koprowski

Sprawozdanie zawiera:

1. Sformułowany ceł ćwiczenia.

2. Krótki opis metody pomiarowej z postacią, konstrukcyjną urządzenia.

3. Tablice z wynikami pomiarów.

4. Wnioski.

Tadeusz Szymik

Wydział: MT

Semestr: IV Grupa: I

Sekcja: II

1. Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie się z pojęciem tensora bezwładności oraz określenie jednej z jego składowych dla korbowodu. Drugą częścią ćwiczenia jest wyznaczenie jednej ze składowych tensora bezwładności metoda drgań skrętnych dla innego elementu.

2. Opis metody pomiarowej.

Rys.1
Rys.2

1. Określamy ciężar korbowodu:

2. Dokonujemy pomiaru odległości l między punktami podwieszenia A i B

(rys.l):

c) Ustawiamy na pryzmie badany element i nadajemy mu ruch drgający o

małym kącie wy chylenia ϕ≤5° (rys.2):

d) Dokonujemy pomiaru czasu 50 pełnych wahnień (powtarzamy to

trzykrotnie):

e) Podwieszamy korbowód w drugim punkcie (B) i powtórnie nadajemy mu

ruch drgający mierżąc równocześnie czas 50 pełnych wahnień (powtarzamy

to trzykrotnie):

f) Obliczamy okres drgań wg wzoru:

7. Wyliczamy długość ramienia b wg wzoru:

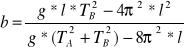
momenty bezwładności odpowiednio względem osi A i B wg wzorów:

oraz moment Is względem środka ciężkości wg wzorów:

I_s=I_A-mb²

I_S=I_A-m*(l-b)²

Drugą część ćwiczenia przeprowadzamy następująco:

a) Dokonujemy pomiaru długości drutu I₀ między punktami zawieszenia (rys.3) oraz jego grubości d₀;

b) Zawieszamy na drucie badany element i nadajemy mu ruch drgający o małym kącie wychylenia ϕ≤5° ;

3. Dokonujemy pomiaru czasu 50 pełnych wahnień (powtarzamy to trzykrotnie):

4. Podwieszamy drugi element o innej masie i powtórnie nadajemy mu ruch drgający mierżąc równocześnie czas 50 pełnych wahnień (powtarzamy to trzykrotnie):

5. Obliczamy okres drgań wg wzoru:

f) Obliczamy wartość momentu bezwładności drutu I₀ wg wzoru:

oraz momenty bezwładności dla poszczególnych elementów wg wzorów:

gdzie G jest stałą równą 8767460
.

Rys.3

3. Wyniki pomiarów i obliczenia.

cześć PIERWSZA.

Dane:

l- 184 mm =0,184 m ;

m = 0,26 kg ;

ϕ= 5" ;

ilość wahnień n = 50 .

Obliczamy ciężar korbowodu:

G=m*g

G=2,55

Lp.	Czas 50 wahnień dla pkt. A [s]	Czas 50 wahnień dla pkt. B [s]
l	35.50	35.16
2	35.22	35.03
3	35.17	35.00
śr	35.30	35.06

Obliczamy okresy drgań:

T_A=0,71[s]

T_B=0,70[s]

obliczamy odległość środka masy osi A:

b=94[mm]

obliczamy moment bezwładności względem pkt. A:

I_A=0,00306[kg*m²]

obliczamy moment bezwładności względem pkt. B:

I_B=0,00284[kg*m²]

obliczamy momenty względem środka ciężkości:

I_S = 0,000763[kg*m² ]

I_S = 0,000734[kg*m²]

czĘŚĆ DRUGA.

Dane:

d₀ = 3.2 mm = 0.32 cm :

l₀ = 480 mm = 0.48 cm;

G = 8767460
;

Lp.	Czas 50 wahnień dla masy I [s]	Czas 50 wahnień dla masy II [s]
l	30.40	42.10
2	30.60	41.70
3	30.50	41.90
śr	30.50	41.90

Obliczamy okres drgań poszczególnych mas:

T_A=0,61[s]

T_A=0,84[s]

Obliczamy wartość momentu bezwładności drutu I₀:

I₀=Π*0,32⁴/32[cm⁴]

oraz momenty bezwładności dla poszczególnych mas:

I₁=1,771[N*cm*s²]

I₂=3,359[N*cm*s²]

4. Wnioski:

DWA MOMENTY BEZWŁADNOŚCI WZGLĘDEM ŚRODKA CIĘŻKOŚCI DLA KORBOWODU POWINNY BYĆ RÓWNE. RÓŻNICA POMIĘDZY NIMI WYNOSI OKOŁO 3%. JEST T0 SPOWODOWANE BŁĘDAMI PODCZAS POMŁAKOW, TAKCIEM POMIĘDZY PRYZMATEM A KORBOWODEM.

---