Badając kryształ antracenu za pomocą synchrotronowego promieniowania rentgenowskiego o długości fali 0.862 nm, maksimum 1-ego rzędu zaobserwowano dla kąta padania 76.1 º. Wyznacz odległość pomiędzy płaszczyznami ułożenia atomów w krysztale. (Wynik podać w Å.) A=1010
![]()
![]()
Kąt graniczny przy przejściu światła monochromatycznego ze szkła do pewnej cieczy wynosi α = 50o. Oblicz długość fali (w nm) w tej cieczy, jeżeli długość fali w szkle wynosi λ = 481 nm.
![]()
Temperatura początkowa ( T1 ) ciała doskonale czarnego uległa zwiększeniu o 78%, przy czym długość fali, na którą przypada maksimum spektralnej zdolności emisyjnej uległa przesunięciu o Δλ = 0.8 µm. Obliczyć temperaturę końcową T2 (K). Stała Wiena b = 2.9·10-3 m·K.
![]()
![]()
![]()
( po podgrzanie) ![]()
Obliczyć pracę wyjścia W elektronu z powierzchni metalu (wynik podaj w eV), jeśli padające nań promieniowanie o długości fali λ = 209 nm wyzwala elektrony o prędkości maksymalnej 6·105 m/s. Masa elektronu m = 9.11·10-31 kg, stała Plancka h = 6.63·10-34 J·s, prędkość światła w próżni c = 3·108 m/s.
![]()
Siatka dyfrakcyjna o N=200 rysach na milimetrze została oświetlona światłem o długości λ=640 nanometrów. Obliczyć kąt ugięcia (w radianach) dla n=2 prążka interferencyjnego.
![]()
![]()
Na siatke dyfrakcyjną, która ma N=414 rys na milimetr, pada prostopadle wiązka światła jednobarwnego o długości fali λ=483.5 nm. Jaki największy rząd nm widma może być obserwowany.
![]()
![]()
![]()
Znaleźć częstotliwość światła (w Hz) wybijającego z powierzchni metalu elektrony całkowicie hamowane przez potencjał 2.1 V. Zjawisko fotoelektryczne rozpoczyna się w tym metalu przy częstotliwości światła padającego 6·1014 Hz. Ładunek elektronu e = 1.6·10-19 C, stała Plancka h = 6.63·10-34 J·s.
![]()
![]()
![]()
Ciało doskonale czarne ma temperaturę T1 = 3130 K. Podczas ostygania tego ciała zmieniła się o Δλ = 5.4 µm długość fali, na którą przypada maksimum spektralnej zdolności emisyjnej. Do jakiej temperatury T2 (K) ostygło ciało. Stała Wiena b = 2.9·10-3 m·K.
![]()
![]()
( po ostyganie) ![]()
Światło o długości fali λ = 603 nm pada na układ dwóch szczelin i tworzy obraz interferencyjny na ekranie odległym o L=1.9 m. Jasny prążek interferencyjny czwartego rzędu znajduje się w odległości y =26.9 mm od prążka centralnego. Policzyć, ile wynosi odległość między szczelinami. Wynik podać w mikrometrach. Założyć, tg=sin= θ.
![]()
![]()
![]()
Antoś stoi nad brzegiem basenu o głębokości h = 2 m i patrzy pionowo w dół. Jaki głęboki wydaje mu się basen (w metrach)? (współczynnik załamania wody n=1.33)
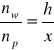
Doświadczenie Younga jest wykonywane z użyciem światła o długości fali λ= 561nm. Odległość miedzy szczelinami jest równa d=0.2 mm, a ekran na którym powstaje obraz interferencyjny jest odległy od szczelin o D=28.9m. Oblicz, jaka jest odległość między ciemnymi prążkami. Wynik podać w centymetrach
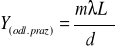
Na kryształ 9-metyloantracenu, w którym odległość między płaszczyznami atomowymi jest równa 8.13 Å, padają promienie rentgenowskie o długości fali 5.48 Å. Przy jakim kącie padania będzie można zaobserwować maxima 1-ego rzędu?
![]()
![]()
Na płytkę szklaną o współczynniku załamania n = 1.72 pada promień świetlny. Jaki jest kąt padania promienia (w stopniach), jeżeli kąt między promieniem odbitym a załamanym wynosi 90o?
![]()
Na płytkę szklaną równoległościenną o współczynniku załamania światła n = 1.7 i grubości d = 1.4 cm pada pod kątem a = 24o promień świetlny. W jakim czasie t (w sekundach) promień ten przejdzie przez płytkę? (prędkość światła w próżni c = 3*108 m/s)
![]()
![]()
![]()
![]()
Znaleźć temperaturę (w K) pieca jeżeli wiadomo, że z otworu o powierzchni 2.1 cm2 promieniuje on w ciągu 1 s energię 10.4 J. Promieniowanie otworu przyjąć za bliskie promieniowaniu ciała doskonale czarnego. Stała Stefana-Boltzmana σ = 5.67·10-8 W/(m2 K4).
![]()
Temperatura ciała doskonale czarnego wynosi 642 K. Po podniesieniu temperatury ciała całkowita moc wypromieniowywana przez ciało zwiększyła się 12 razy. O ile stopni (K) podwyższono temperaturę ciała?
![]()
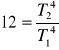
![]()
Powierzchnia płytki wolframowej jest naświetlana promieniowaniem o długości fali λ = 195 nm. Praca wyjścia elektronu z wolframu W = 4.55 eV. Jakie napięcie hamujące U (w V) należy przyłożyć do płytki, aby prąd fotoelektryczny przestał płynąć? Ładunek elektronu e = 1.6·10-19 C, stała Plancka h = 6.63·10-34 J·s, prędkość światła w próżni c = 3·108 m/s.
![]()
![]()
![]()
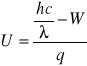
Średnica spirali wolframowej w elektrycznej lampie oświetleniowej wynosi d = 0.2 mm, zaś długość l = 14 cm. Lampa jest włączona do sieci obwodu elektrycznego o napięciu U = 220 V i przez lampę płynie prąd o natężeniu i = 0.3 A. Obliczyć temperaturę spirali, zakładając że ciepło jest tracone jedynie przez wypromieniowanie, przy czym całkowita zdolność emisyjna spirali wolframowej wynosi k = 0.41 całkowitej zdolności emisyjnej ciała doskonale czarnego w tej temperaturze. Stała Stefana-Boltzmanna σ = 5.67·10-8 W/(m2 K4).
![]()
![]()
![]()
Foton promieniowania rentgenowskiego o długości fali λ = 0.448 Å zderza się ze swobodnym elektronem pozostającym początkowo w spoczynku. W wyniku tego zderzenia foton rozpraszany jest do tyłu, a elektron odrzucany jest do przodu. Obliczyć energię kinetyczną jaką nabył elektron w wyniku tego zderzenia. Wynik podaj w keV. Masa elektronu m = 9.11·10-31 kg, stała Plancka h = 6.63·10-34 J·s, prędkość światła w próżni c = 3·108 m/s, comptonowska długość fali dla rozproszenia comptonowskiego na elektronie λc = 0.0243 Å. Kat =180
![]()
![]()
Znaleźć długość fali promieniowania (wynik podaj w mikrometrach) wybijającego z powierzchni metalu elektrony całkowicie hamowane przez potencjał 0.8 V. Zjawisko fotoelektryczne rozpoczyna się w tym metalu przy częstotliwości światła padającego 5.6·1014 Hz. Ładunek elektronu e = 1.6·10-19 C, stała Plancka h = 6.63·10-34 J·s.
![]()
![]()
Energia promieni rentgenowskich wynosi 111 keV. Znaleźć kąt rozproszenia, jeśli długość fali promieni rentgenowskich po rozproszeniu comptonowskim zmieniła się o 26 %. Masa elektronu m = 9.11·10-31 kg, stała Plancka h = 6.63·10-34 J·s, prędkość światła w próżni c = 3·108 m/s, comptonowska długość fali dla rozproszenia comptonowskiego na elektronie λc = 2.43 pm.
![]()
![]()
![]()
Obliczyć maksymalną energię kinetyczną, którą może uzyskać swobodny i spoczywający elektron po zderzeniu z fotonem o długości fali λ = 39 pm. Wynik podaj w keV. Masa elektronu m = 9.11·10-31 kg, stała Plancka h = 6.63·10-34 J·s, prędkość światła w próżni c = 3·108 m/s, comptonowska długość fali dla rozproszenia comptonowskiego na elektronie λc = 2.43 pm. Kat=180=-1
![]()
![]()
W zjawisku Comptona energia padającego fotonu rozdziela się w równych częściach między foton rozproszony i elektron odrzutu. Kąt rozproszenia jest równy 125o. Wyznaczyć kąt pomiędzy padającym fotonem a elektronem odrzutu. Masa elektronu m = 9.11·10-31 kg, stała Plancka h = 6.63·10-34 J·s, prędkość światła w próżni c = 3·108 m/s, comptonowska długość fali dla rozproszenia comptonowskiego na elektronie λc = 0.0243 Ǻ.
![]()
![]()
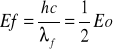
![]()
![]()
![]()
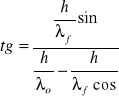
Na układ polaryzatorów pada wiązka światła niespolaryzowanego. Jaki jest kąt między polaryzatorem P2 oraz P3 jeżeli stosunek natężenia światła wychodzącego z polaryzatora P2 do natężenia światła wchodzącego do tego polaryzatora wynosi 0.98. Wychodząca wiązka światła po przejściu przez cały układ stanowi 31% natężenia światła wpadającego do układu.
![]()
![]()
|
α |
β |
|
|
|
|
|
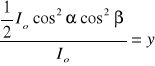
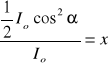
Wyszukiwarka
Podobne podstrony:
Kontrola badań laboratoryjnych
badania laboratoryjne 6
ROZRÓD Badanie terenowe i laboratoryjne mleka
Diagnostyka laboratoryjna chorób serca i mięśni poprzecz (2)
Diagnostyka laboratoryjna zaburzen gospodarki lek 2010
medycyna laboratoryjna
Medycyna laboratoryjna 12 13
7) Laboratoria EMG i MMG na pziomach sily i ko
3 1 5 CCNA1 Laboratorium pl
laboratorium2
2012 KU W5 tryb dzienny moodle tryb zgodnosci
Laboratorium 7
Laboratorium jezyk c4 2013
więcej podobnych podstron