Nazwy proste - składające się tylko z jednego wyrazu

Nazwy złożone - składające się z więcej niż jednego wyrazu

Nazwa konkretna - desygnatem jest osoba, rzecz lub coś co sobie wyobrażamy jako rzecz lub osobę (krasnoludek, UFO)

Nazwa abstrakcyjna - to nazwa dla zdarzenia (wypadek) lub stanu rzeczy (cisza); albo cechy (białość, szarość); albo stosunku (braterstwo).

Nazwy generalne - zostały nadane swoim desygnatom ze względu na ich cechy (dom)

Nazwy indywidualne - desygnat z pominięciem cech które on posiada. (Zofia

Konstytutywny zespół cech (cechy konstytutywne) - to taki zespół cech, który wystarczy by odróżnić desygnaty danej nazwy od innych przedmiotów.

Cechy konsekutywne - są to wszystkie pozostałe, mniej ważne cechy po wyłączeniu cech konstytutywnych.

Nazwy Ogólne - mają więcej niż jeden desygnat - szafa, koń, żołnierz.

Nazwy jednostkowe - mają tylko jeden desygnat - naturalny księżyc naszej planety, najdłuższa rzeka w Polsce.

Nazwy puste (bezprzedmiotowe) - to takie, które wcale nie mają desygnatów - stupiętrowy dom w Poznaniu, syn bezdzietnej matki. Nazwy puste niczego nie oznaczają, niemniej coś znaczą; jeśli są nazwami generalnymi, mają pewną treść, każą mianowicie szukać (jeśli są konkretne) osób czy rzeczy o określonych cechach, tyle tylko, że przedmiotów o takich cechach nie ma lub być nie może.

Nazwy zbiorowe - nazwy, których desygnatami są nie poszczególne rzeczy, lecz takie przedmioty które traktujemy jako agregaty złożone z poszczególnych rzeczy.

Nazwa ostra - bez wątpliwości rozstrzygnąć o każdym napotkanym przedmiocie, z którym odpowiednio zapoznaliśmy się, czy jest on desygnatem pewnej określonej nazwy.

Nazwa nieostra - o pewnych napotkanych przedmiotach, mimo dobrego zapoznania się z ich cechami, nie umiemy orzec czy są desygnatami danej nazwy.

Nazwa niewyraźna - nie można podać zespół cech wystarczających dla odróżnienia desygnatów danej nazwy od innych przedmiotów.

Nazwa wyraźna - można podać zespół cech wystarczających dla odróżnienia desygnatów danej nazwy od innych przedmiotów.

Rodzaje stosunków między zakresami nazw:

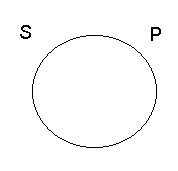
1. Stosunek zamienności - istnieją przedmioty, które są jednocześnie desygnatami nazwy S i nazwy P. (nie ma takich desygnatów nazwy S które nie byłyby desygnatami nazwy P).

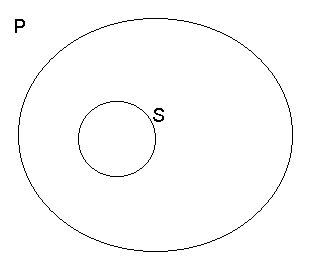
2. Stosunek Podrzędności zakresu nazwy S względem zakresu nazwy P.

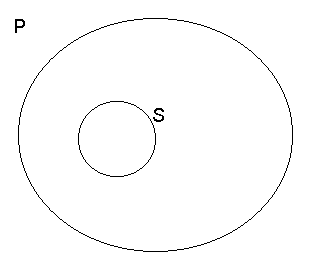
3. stosunek nadrzędności zakresu nazwy S względem zakresu nazwy P.

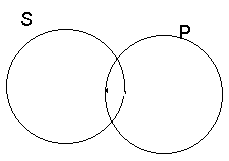
4. Stosunek krzyżowania się zakresów nazw.

5. Stosunek wykluczania się zakresów nazw.

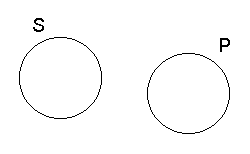
Wykluczanie się zakresów nazw:

• w stosunku sprzeczności:

sędzia / nie-sędzia

pies / nie-pies

• w stosunku przeciwieństwa

pies / kot

Definicja

Definicja realna - termin definicja używamy dla oznaczenia zespołu zdań podających charakterystykę (przysługujących temu i tylko temu)

Definicja nominalna - jest wyrażeniem, które podaje informacje o znaczeniu jakiegoś terminu.

Różnice pomiędzy definicją realną a nominalną:

• def. nominalne wypowiadane są co najmniej w II stopniu języka;

• def. realne wypowiadane są w języku przedmiotowym

• def. realne wszystkie są zdaniami w sensie logicznym, bo są albo prawdziwe, albo fałszywe - opisują rzeczywistość

def. nominalne tylko niektóre są zdaniami w sensie logicznym - mianowicie te, które stwierdzają jakie znaczenie ma/miał termin definiowany.

Natomiast definicje nominalne ustalające jak będziemy używać danego terminu w przyszłości w projektowanym sposobie mówienia nie są zdaniami w sensie logicznym bo nie są ani prawdziwe ani fałszywe - nie opisują rzeczywistości.

Definicja sprawozdawcza - zdaje sprawozdanie (relację) z tego jaki jest/był sposób posługiwania się wyrażeniem

Definicja projektująca - ustala znaczenie terminu na przyszłość. Nie jest ani prawdziwa ani fałszywa.

• definicja konstrukcyjna

• definicja regulująca

definicja tego terminu albo oddaje dotychczasowe wyraźne znaczenie (i wówczas jest to definicja sprawozdawcza) albo definiuje dany termin odmiennie - i wówczas jest definicją konstrukcyjną, bo nie liczy się z dotychczasowym znaczeniem definiowanego terminu.

Jeżeli nazwa jest niewyraźna to definicja danej nazwy, która odzwierciedla daną niewyraźność jest definicją sprawozdawczą.

Definicja równościowa:

definiendum zwrot zdefiniowany

łącznika

definiensa (części definiującej).

(Np. Wyraz „jabłko” oznacza owoc jabłoni.

Definiendum - wyraz „jabłko”

Łącznik - oznacza

Definiens - Owoc jabłoni)

• Definicja klasyczna - (jest definicją równościową) - zawiera wyraz definiowany, genus - rodzaj, do którego należy gatunek przedmiotów definiowanych; oraz differentia specifica - różnica gatunkowa.

- wskazuje treść i zakres

• Definicja nieklasyczna - wskazuje zakresy nazw, które w sumie dają zakres nazwy definiowanej.

(np. A znaczy/oznacza/jest to P lub R lub S)

Definicja nierównościowa:

• Definicją przez postulaty - definicją aksjologiczną - wyrażenia „W” nazywamy zespół zdań o następujących właściwościach:

1. W zdaniach tych występuje wyrażenie „W”

2. pozostałe wyrażenia występujące w tych zdaniach mają ustalone znaczenie.

3. Wyrażenie „W” należy tak rozumieć, by zdania w których ono występuje zmieniały się wszystkie jednocześnie w zdania prawdziwe.

(Np. „W” jest zielone”/ „W” rośnie na łące/ „W” jedzą krowy/ Czterolistne „W” przynosi szczęście.)

• Definicje cząstkowe to zdanie lub zespół zdań, które co prawda nie dają rozstrzygnięcia iż daną nazwą definiowaną oznacza się wszystkie przedmioty danego typu, i tylko przedmioty danego typu; ale podają one niektóre tzw. pozytywne albo negatywne kryteria stosowalności nazwy definiowanej; albo wskazują one na to, że desygnatami nazwy są z pewnością takie a takie przedmioty, a może również inne (pozytywne kryteria stosowalności - wrona jest czarna) albo na to że desygnatami nazwy z pewnością nie są przedmioty określonego rodzaju, a być może również inne (negatywne kryteria stosowalności - wrona nie jest rybą).

Zespół definicji cząstkowych trafnie dobranych tworzy definicję przez postulaty.

Błędy w definicjach

Ignotum per Ignotum - nieznane przez nieznane - wyraz definiowany jest nieznany odbiorcy, definiens również jest nieznany odbiorcy.

-jest to błąd względny i subiektywny

Idem per Idem - to samo przez to samo - w definiendum i w definiensie powtarza się ten sam zwrot (powtórzono wprost zwrot zawarty w definiendum).

-jest to błąd bezwzględny i obiektywny

-jest to błędne koło bezpośrednie.

-jeśli popełnia się ten błąd, jednocześnie popełnia się błąd ignotum per ignotum

Błędne koło pośrednie - zespół definicji, w których pierwsza definicja odsyła do drugiej, a druga z powrotem do pierwszej (np. logika to nauka o poprawnym myśleniu / poprawne myślenie to myślenie logiczne / myślenie logiczne to myślenie zgodnie z prawami logiki)

Błąd przesunięcia kategorialnego - w definiendum jest inna kategoria ontologiczna niż w definiensie.

• definiendum i definiens wykluczają się.

Defininicja za szeroka - zakres definiensa obejmuje również przedmioty nie należące do definiendum

- prokurator (S) to pracownik prokuratury (P)

Definicja za wąska - zakres definiensa nie obejmuje wszystkich przedmiotów należących do zakresu definiendum.

- ołówek (S) to przyżąd do pisania złożony z pręcika grafitowego umieszczonego w niebieskiej oprawce (P)

W definicjach konstrukcyjnych nie występuje błąd definicji za wąskiej lub definicji za szerokiej. Błędy te można popełnić tylko w definicjach równościowych sprawozdawczych.

Błąd krzyżowania się zakresów.

Podział zbiorów:

Wymóg rozłączności

Jest spełniony kiedy dwa dowolne podzbiory wzajemnie się wykluczają.

Wymóg adekwatności

Wymóg zupełności jest spełniony kiedy suma wszystkich wyróżnionych podzbiorów jest identyczna ze zbiorem z którego wyróżniono te podzbiory.

1. Podział nieskończony i skończony (określona liczba elementów tego zbioru)

2. Podział wedle pewnej zasady (podział na płcie i ze względu na kolor włosów).

1. muszą zostać uwzględnione wszystkie odmiany danej cechy (spełniony gdy wymienione są wszystkie elementy)

2. cecha, która stanowi podstawę podziału musi przysługiwać wszystkim elementów dzielonego wzoru

3. żaden element dzielonego wzoru nie posiada dwóch odmian cechy

gdzie: a i b - wymóg adekwatności c - wymóg rozłączności

3. Podział dychotomiczny (wyróżniamy w zbiorze dzielonym człon składającym się z elementów zawierających pewną cechę i człon składający się z pozostałych elementów (np. studiujący i niestudi) Wymóg rozłączności i adekwatności jest gwarantowany przez

prawa logiczne

Zasada wyłączonego środka:

p \/~ p (p lub nie p)

Zasada sprzeczności:

~ (p /\ ~p) (nie jest tak, że jednocześnie p i nie p)

Pojęcie zdania i rachunek zdań

Zdaniem w sensie logicznym nazywamy wyrażenie, które jest prawdziwe lub fałszywe. Prawda i fałsz to tzw. wartości logiczne (inaczej, zdaniem w sensie logicznym określamy wyrażenie, które ma wartość logiczną).

Np. 24 grudnia 2010 roku temp w Warszawie będzie wynosiła -10

Pytania i rozkazy nie mają wartości logicznej, ponieważ nie można przypisać im prawdy i fałszu.

Jest takie wyrażenie za które wolno wstawić dowolne zdanie [cośtam].

Czyli, jeśli w pewnym wyrażeniu mamy kilka różnych zmiennych zdaniowych to za każdą z nich wolno wstawić dowolne zdanie. Natomiast jeśli jedna zmienna występuje w danym wyrażeniu kilka razy to nie wolno w jej miejsce wstawiać różnych zdań.

Krzysztof studiuje kulturoznawstwo lub Anna studiuje historię ( p v r)

\/ /\ - prawdziwościowe spójniki zdania. Są to takie wyrażenia, które łączą dwa zdania albo łączą się tylko z jednym zdaniem tworząc zdania złożone, których wartość logiczna zależy jedynie od wartości logicznej zdań łączonych.

~ - spójnik negacji tworzy zdania prawdziwe gdy następują po nich zdania fałszywe, a zdania fałszywe gdy następują po zdaniach prawdziwa.

/\ - spójnik koniunkcji tworzy zdanie prawdziwe tylko wtedy kiedy oba połączone zdania są zdaniami prawdziwymi

p \/ r - spójnik alternatywy jest spójnikiem prawdziwościowym w trzech układach:

1. Kiedy pojawia się jako wyrażenie co najmniej jedno z dwojga. Zawsze wtedy tworzy zdania prawdziwe z wyjątkiem gdy łączy oba zdania fałszywe

2. Gdy pojawia się jako wyrażenie co najwyżej jedno z dwojga. Wówczas tworzy zdania prawdziwe zawsze z wyjątkiem sytuacji gdy są dwa zdania prawdziwe.

3. Gdy pojawia się jako wyrażenie dokładnie jedno z dwojga. Wówczas tworzy zdania prawdziwe tylko wtedy gdy jedno zdanie jest prawdziwe a drugie fałszywe.

Spójniki prawdziwościowe noszą nazwę funktorów ekstensjonalne co znaczy, że posiadają taką właściwość, która pozwala stwierdzić, że wartość logiczna stworzona przy ich użyciu zdań zależy tylko i wyłącznie od wartości logicznej tworzących jej wyrażeń.

Spójniki nieprawdziwościowe czyli tzw. Funktory intensjonalne. Odznaczają się tym, że wartość logiczna stworzona przy ich użyciu zdań nie zależy tylko od wartości logicznej zdań składowych lecz także od ich treści.

Spójniki prawdziwościowe przypominają nam znaki działań algebraicznych co znaczy, że jeśli znamy wartość logiczną poszczególnych zdań składowych, możemy obliczyć wartość całego zdania. Na tym polega rachunek zdania.

Rachunek zdań

Symbol	Schemat zdań	Sposób czytania	Nazwa zdania złożonego
~	~p	nie jest prawdą że p	negacja
/\	p /\ r	p i r	koniunkcja
\/	p \/ r	p lub r	alternatywa
→	p → r	jeśli p to r	implikacja
≡	p ≡ r	p wtedy i tylko wtedy gdy r	równoważność

MATRYCA NEGACJI

p	q
1	1
0	1

Negacja jest prawdziwa wtedy i tylko wtedy gdy jej argument jest fałszywy i odwrotnie gdy argument jest prawdziwy.

Zdanie zanegowane, czyli dołączone do spójnika negacji

jako jego argument wraz z negacją czyli zdaniem powstałym po zanegowaniu tamtego zdania tworzą zdania wzajemnie sprzeczne.

MATRYCA KONIUNKCJI

p	q	p/\q
1	1	1
1	0	0
0	1	0
0	0	0

Koniunkcja jest prawdziwa wtedy i tylko wtedy gdy oba argumenty są prawdziwe a fałszywa gdy przynajmniej jeden z jej argumentów jest fałszywy.

MATRYCA ALTERNATYWY

p	q	p\/q
1	1	1
1	0	1
0	1	1
0	0	0

Alternatywa jest prawdziwa wtedy i tylko wtedy gdy przynajmniej jeden z jej argumentów jest prawdziwy.

MATRYCA IMPLIKACJI

W przypadku implikacji istotna jest kolejność argumentów

P - poprzednik implikacji Q - następnik implikacji

p	q	p→q
1	1	1
1	0	0
0	1	1
0	0	1

Implikacja jest fałszywa wtedy i tylko wtedy gdy poprzednik jest prawdziwy a następnik jest fałszywy.

Z tej implikacji wynika, że zawsze gdy poprzednik jest fałszywy niezależnie od następnika implikacja jest prawdziwa i jednocześnie zawsze prawdziwa jest implikacja o prawdziwym następniku niezależnie od poprzednika.

Implikacja jest prawdziwa wtedy i tylko wtedy gdy jej poprzednik jest fałszywy lub jej następnik jest prawdziwy. P → q ≡ ~p \/ q

MATRYCA RÓWNOWAŻNOŚCI

p	q	p≡q
1	1	1
1	0	0
0	1	0
0	0	1

Prawdziwa tylko gdy oba jej człony mają taką samą wartość logiczną.

ALTERNATYWA ROZŁĄCZNA

p	q	p\/q
1	1	0
1	0	1
0	1	1
0	0	0

Jest prawdziwa wtedy i tylko wtedy gdy jej argumenty mają różną wartość logiczną a fałszywa gdy mają taką samą wartość.

P \/ q = ~(p=q)

MATRYCA DYSJUNCJI

p	q	p \ q
1	1	0
1	0	1
0	1	1
0	0	1

Jest fałszywa wtedy i tylko wtedy gdy oba jej człony są prawdziwe w pozostałych xx jest prawdziwa.

Funktor łącznej negacji (ani p ani q)

Łączna negacja jest prawdziwa wtedy i tylko wtedy gdy obydwa jej argumenty są fałszywe natomiast jest fałszywa gdy przynajmniej jeden z argumentów jest prawdziwy.

Wnioskowanie w logice

Sposób rozumowania, w którym na podstawie pewnych posiadanych przez nas przekonań możemy dojść do innego wniosku.

1. Przesłanka wnioskowania - zdanie wyrażające jedno z przekonań wyjściowych

2. Wniosek - zdanie, które wywnioskowaliśmy z przesłanek

Wnioskowanie dedukcyjne

Wnioskowanie, z którego przesłanek wynika logicznie wniosek.

Wnioskowanie dedukcyjne jest wtedy i tylko wtedy, gdy implikacja, której poprzednik stanowi koniunkcję wszystkich przesłanek tego wnioskowania, a następnik stanowi wniosek tego wnioskowania jest tautologią.

MODUS PONENDO PONENS - sposób przez potwierdzenie potwierdzające

Wnioskowanie niededukcyjne

Wnioskowanie, z którego przesłanek nie wynika logicznie wniosek, natomiast możemy powiedzieć, że w mniejszym lub większym stopniu przesłanki uprawdopodobniają wniosek. Czyli, nie dysponujemy 100% pewnością, natomiast można dyskutować o stopniu prawdopodobieństwa.

Podstawowy podział:

1. Wnioskowanie redukcyjne - wnioskowanie niededukcyjne, którego przesłanki wynikają logicznie z wniosku albo, którego pewne przesłanki wynikają logicznie z koniunkcji wniosku i innych jego przesłanek.
   (między przesłankami a wnioskiem zachodzą pewne związki logiczne)

2. Wnioskowanie przez indukcję nienumeracyjną niezupełne - wnioskowanie, niededukcyjne, w którym dochodzi się do wniosku opisującego jakąś ogólną prawidłowość wychodząc od przesłanek opisujących pewne jednostkowe przypadki tej prawidłowości

3. Wnioskowanie przez analogię - jest to, w których od przesłanek przypisujących wskazanym obiektom jakiegoś rodzaju cechę dochodzi się do wniosku przypisującego tę cechę kolejnym obiektom tego rodzaju.

MODUS TOLLENDO TOLES - sposób przez zaprzeczenie

---