Geodezja - nauka i dziedzina techniki, zajmująca się uzyskiwaniem informacji o elementach środowiska geograficznego, kształcie i wymiarach Ziemi.

Zadania geodezji:

• Badanie kształtu Ziemi, rozmiarów oraz stanu i zmian środowiska geograficznego,

• Dostarczenie danych dla systemów informacji przestrzennej

• Przenoszenie projektów i planów w teren

• Sporządzanie i gromadzenie dokumentacji geodezyjnej oraz jej udostępnianie zainteresowanym osobom

Do prac geodezyjnych należą:

• Projektowanie i wykonywanie pomiarów geodezyjnych

• Dokonywanie obliczeń

• Sporządzanie dokumentacji geodezyjnej

• Zakładanie i aktualizacja baz danych

• Sporządzanie zdjęć, pomiary i opracowania związane z realizacją zadań w dziedzinie geodezji i kartografii oraz krajowego Sit

Działy geodezji:

• Geodezja ogólna

• Geodezja wyższa

• Kartografia

• Topografia

• Fotogrametria

• Instrumentaloznawstwo geodezyjne

• Rachunek wyrównawczy

• Geodezja gospodarcza

• Geodezja dynamiczna

• Astronomia geodezyjna

Miary długości - podstawową jednostką długości przyjętą na całym świecie jest metr, stanowiący w przybliżeniu 10^-7 ćwiartki południka ziemskiego.

Miary pola powierzchni - podstawową jednostką pola jest metr kwadratowy.

Jednostki wielokrotne to ar, hektar i kilometr kwadratowy.

Miary kąta - miara łukowa kąta - w SI obowiązującą miarą kąta płaskiego jest jednostka miary łukowej - radian, czyli kąt, którego długość łuku równa jest promieniowi jakim zatoczono ten łuk. Miara łukowa dla kąta pełnego wynosi 2Π.

Podział gradowy kąta - jednostką podstawową podziału gradowego jest kąt prosty, który podzielono na 100 równych części, zwanych gradami. Kąt pełny to 100^g.

Mapa - płaski obraz powierzchni Ziemi. Przedstawia w pomniejszeniu w sposób umowny, a jednocześnie matematycznie określony, na którym za pomocą ustalonych znaków oddaje się wybraną treść.

Skala mapy - stosunek długości pewnego odcinka na mapie do długości poziomej odpowiadającego mu odcinka w terenie.

1/M = d/D 1- jednostka skali mapy M - mianownik skali mapy d- długość odcinka na mapie w skali 1:M

D - długość odcinka pomierzonego w terenie

Podziałka - graficzne przedstawienie skali.

Podziałka liniowa - przedstawia linię prostą podzieloną na równe części. Pierwszy odcinek tej prostej dzielimy jeszcze na pewną liczbę równych części i nazywamy podstawą podziałki. Podziałkę opisujemy w wartościach terenowych.

Podziałka poprzeczna - sporządzamy ją celem zwiększenia dokładności podziałek.

(transwersalna)

Celowa - linia celowania, łącząca środek siatki celowniczej lunety instrumentu geodezyjnego i punktu celu.

Sygnały - służą do uwidocznienia położeniaodległych punktów. Do sygnalizacji punktów używane są tyczki lub tarcze celownicze na takich samych statywach i podstawkach jak teodolit.

POMIAR KĄTÓW

Pomiar kątów poziomych metodą kierunkową

Metoda ta polega na celowaniu do kolejnych punktów P1, P2, P3, P4, które wyznaczają pęk prostych, wychodzących ze stanowiska S i wykonywaniu w I i II położeniu lunety odczytów kierunków dla tych punktów oraz określaniu kierunków zredukowanych k1, k2, k3, k4.

Pomiar kątów metodą repetycyjną

Polega on na powtarzaniu pewnych czynności pomiarowych dla otrzymania na limbusie całkowitej wielokrotności mierzonego kąta.

m - ilość pełnych obrotów limbusa

n - ilość repetycji

O_P - odczyt prawy w II położeniu lunety

O_L - odczyt lewy w I położeniu lunety

1. Po czynnościach wstępnych celujemy na lewe ramię kąta. Zapisujemy odczyt.

2. Obracamy alidadę zgodnie z ruchem wskazówek zegara i celujemy na prawe ramię kąta. Wykonujemy odczyt orientacyjny. W ten sposób po raz pierwszy odłożyliśmy kąt.

3. Odkładamy kąt n-razy w dwóch położeniach luney.

POMIAR KĄTÓW PIONOWYCH

Kąt pionowy - kąt, którego obydwa ramiona leżą na płaszczyźnie pionowej, przy czym jedno ramię jest zawsze stałe, a drugie ramię zmienne, wyznaczane przez oś celową teodolitu, kierowaną do wybranego punktu celu P.

Wyróżniamy dwa rodzaje kątów pionowych:

• Kąt pionowy horyzontalny - kąt pomiędzy horyzontem instrumentu, a osią celową lunety teodolitu.

• Kąt pionowy zenitalny - kąt pomiędzy płaszczyzną pionową skierowaną ku zenitowi, a osią celową. Suma obydwu rodzajów kątów pionowych daje nam kąt prosty.

Powierzchnia odniesienia - powierzchnia, na którą rzutuje się pomierzone punkty.

Geoida - teoretycznapowierzchnia najlepiej oddająca rzeczywisty kształt powierzchni ziemi, wykorzystywana jako powierzchnia odniesienia dla pomiarów wysokościowych.

Obowiązującym dla Polski jest poziom morza określony przez zero łaty wodowskazu stacji mareograficznej w Kronsztadzie koło Sanki Petersburga.

Elipsoida obrotowa - powierzchnia odniesienia wykorzystywana dla określenia położenia sytuacyjnego punktów na Ziemi.

POMIARY

Sytuacyjny - zespół czynności technicznych pozwalających na określenie kształtu i wielkości, rodzaju i wzajemnego położenia szczegółów terenowych, umożliwiających wyznaczenie współrzędnych prostokątnych płaskich punktów tych szczegółów, a tym samym przedstawienie ich obrazów w rzucie prostokątnym na powierzchnię odniesienia.

Wysokościowy - zespół czynności technicznych określających wysokość względem przyjętego poziomu odniesienia.

Osnowa geodezyjna- usystematyzowany zbiór punktów geodezyjnych utrwalonych w terenie, dla których określona została dokładność usytuowania oraz wzajemne położenie.

Sieć geodezyjna - zbiór punktów geodezyjnych, stanowiących odrębną całość, charakteryzującą się jednolitością metod pomiarów i sposobem określenia położenia tych punktów.

Podział osnów ze względu na rolę i znaczenie dla prac geodezyjnych:

• Osnowy podstawowe

• Osnowy szczegółowe

• Osnowy pomiarowe

Ze względu na sposób przedstawienia położenia punktów osnowy geodezyjne dzielmy na:

• Osnowę poziomą

• Osnowę pionową

Ze względu na dokładność wyrażoną przez klasę osnowy wyróżniamy następujące podziały:

• Sieć klasy I

• Sieć klasy II

• Sieć klasy III

Niwelacja - pomiar wysokościowy, jest to zespół czynności technicznych, które pozwalają na określenie wysokości punktów względem przyjętego poziomu odniesienia i umożliwiających przedstawienie form ukształtowania terenu.

Reper - punkt o znanej wysokości oznaczony w terenie.

Powierzchnią odniesienia dla pomiarów wysokościowych jest geoida zerowa. Punktu położone na jej powierzchni mają wysokość zerową. Wysokości liczone względem geoidy zerowej noszą nazwę wysokości bezwzględnych.

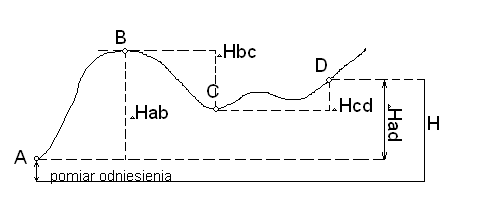
W oparciu o znaną wysokość punktu początkowego A i wyliczoną lub pomierzoną różnicę wysokości można uzyskać wysokość punktu B.

H_B = H_A + ΔH_AB

Jeśli mamy różnicę wysokości pomiędzy sąsiednimi parami punktów, możemy obliczyć wysokości punktów pośrednich oraz punktu końcowego.

H_D = H_A + ΔH_AB + ΔH_BC + ΔH_CD = H_A + [ΔH]

Metody pomiarów wysokościowych

W zależności od celu niwelacji wyróżniamy:

• Niwelację reperów

• Niwelację podłużną i poprzeczną (przekrojów)

• Niwelację powierzchniową

Niwelacja geometryczna - polega na obliczeniu różnicy wysokości pomiędzy punktami A i B na podstawie różnicy odległości pionowych t i p danych punktów, a zbudowaną ponad powierzchnią terenu płaszczyzną poziomą. Dzielimy ją na niwelację precyzyjną i techniczną.

Niwelator - instrument geodezyjny, który za pomocą spoziomowanej osi celowej lunety Kub wiązki laserowej realizuje płaszczyznę poziomą.

Łaty niwelacyjne - przymiary sztywne służące do wyznaczenia odległości pionowych między niwelacyjnymi punktami, a płaszczyzną poziomą zakreśloną przez oś celową niwelatora.

Budowa niwelatora samopoziomujące optycznego: spodarka, 3 śruby poziomujące, libela okrągła, lusterko, alidada, luneta, śruba ogniskująca, leniwka

Niwelacja geometryczna za środka

Polega na ustawieniu niwelatora nad punktem S, który znajduje się w środku odcinka wyznaczonego przez punkty A i B, na których stoją łaty.

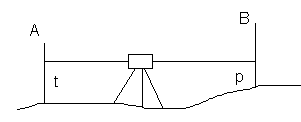
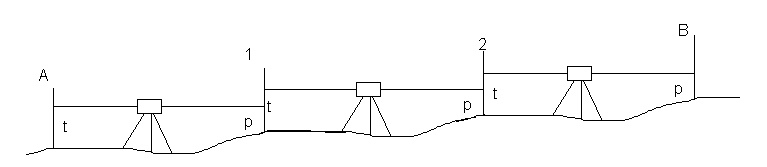
Gdy punkty niwelacyjne są daleko od siebie, odległość między nimi dzieli się na mniejsze odcinki, tworząc ciąg niwelacyjny.

OBLICZANIE POLA POWIERZCHNI

„Działkę ewidencyjną stanowi ciągły obszar gruntu, położony w granicach jednego obrębu, jednorodny pod względem prawnym, wydzielony z otoczenia za pomocą linii granicznych”

Metody obliczania pól:

• analityczna - na podstawie współrzędnych lub miar pozyskanych bezpośrednio w terenie

• graficzna - na podstawie danych z mapy

• kombinowana - część danych z terenu, a część z mapy

• mechaniczna - za pomocą planimetru biegunowego

• automatyczna - mapa numeryczna + urządzenia

Metoda analityczna

Wierzchołki figury, której pole chcemy obliczyć numerujemy zgodnie z ruchem wskazówek zegara.

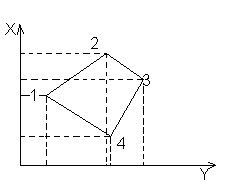
x₂ Możemy przyjąć, że podstawy to współrzędne x,

a wysokość współrzędne y.

x₃

x₁

2P = Σ X₁ (Y_i+1 + Y_i-1)

x₄ -2P = Σ Y₁ (X _i+1 + X _i-1)

y₁ y₂ y₄ y₃

Metoda graficzna

Polega na wyznaczeniu pola figury naniesionej na mapie w oparciu o pomiar graficzny elementów potrzebnych do obliczeń. Pomiary na mapie poprzedza najczęściej podział danego obiektu na proste figury geometryczne.

Metoda mechaniczna

Planimetr biegunowy składa się z: ramienia biegunowego, ramienia wodzącego i licznika obrotów. Odczyt składa się z czterech cyfr.

Wyznaczanie stałej planimetru - ustawiamy planimetr na zewnątrz figury, której pole można obliczyć ze wzorów. Obieramy punkt początkowy na obwodzie figury, dokładnie ustawiamy w nim wodzik i zerujemy kółko całkujące lub notujemy odczyt wyjściowy n. Obwodzimy kontur w prawo, powracając do punktu początkowego. Notujemy odczyt końcowy n2. Obwodzimy m-razy kontur i notujemy odczyty. Obliczamy pole figury na podstawie współrzędnych wierzchołków. Obliczamy wartość n_śr (n₂-n₁)/m i P_z (pole planimetrowanej figury).Stałą planimetru k wyznaczamy ze wzoru k=P_z/n_śr.

P_z = k * (n₂ - n₁)

n_śr = Σ (n₂ - n₁)/m

k = P_z : n_śr

Metoda analityczna

Skalujemy mapę, kalibrujemy i na podstawie skanu tworzymy mapę numeryczną. Pole powierzchni możemy wyznaczać również za pomocą planimetrów elektronicznych.

POMIAR DŁUGOŚCI

Tyczenie linii prostej - zagęszczanie punktami pośrednimi boku zawartego pomiędzy dwoma zadanymi punktami, które zostały w ustalony sposób zaznaczone i utrwalone w terenie.

1. Tyczenie sposobami bezpośrednimi

Tyczenie w terenie odcinka prostej, określonego przez dwa zadane punkty A i B polega na wyznaczeniu w odstępach nie przekraczających zwykle 50 m pewnej ilości punktów pośrednich, leżących na tej samej płaszczyźnie pionowej, co punkty A i B.

Tyczenie w przód

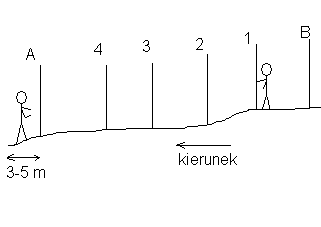
Pierwszą czynnością jest zasygnalizowanie tyczkami punktów końcowych odcinka A i B. Obserwator ustawiony w odległości 3-5 m od punktu początkowego patrzy na tyczki skrajne i wskazuje pomiarowemu za pomocą rąk kierunek przesunięcia trzymanej przez niego tyczki do momentu uzyskania jej pokrycia się z tyczkami A i B.

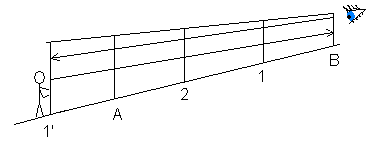
Tyczenie przedłużenia prostej (wstecz)

Przedłużaną prostą jest AB. A1' - przedłużenie prostej AB.

Tyczenie punktu przecięcia się prostych

Na prostych AB i CD wytycza się przynajmniej po 1 punkcie pośrednim. Następnie pomiarowy naprowadzany jest przez dwóch obserwatorów, których kolejne wskazania doprowadzają tyczkę pośrednią E do pokrycia się z tyczkami AB i CD. Na prostych AB i CD wytycza się po 2 punkty pośrednie położone blisko siebie, lecz po przeciwnych stronach punktu E. Pomiędzy wyznaczonymi punktami rozciąga się sznurki, na ich przecięciu leży szukany punkt.

Tyczenie przez wzniesienie

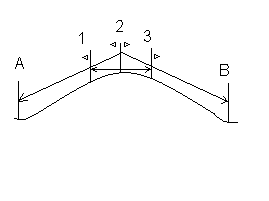
Istota metody ze środka polega na ustawieniu obserwatorów wewnątrz tyczonego odcinka AB na kilku punktach pośrednich, gdzie na przemian dokonują oni wzajemnych wskazań przesunięć tych tyczek. Cechą charakterystyczną jest brak wzajemnej widoczności pomiędzy końcami odcinka prostej. Ilość wytyczanych punktów pośrednich zależy od liczby i osób mogących brać udział w tyczeniu.

tyczenie prostej metodą „ze środka” przy 3 punktach pośrednich

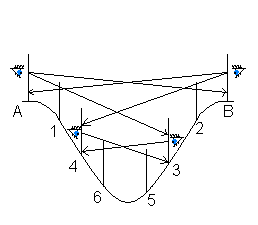
Tyczenie prostej przez wąwóz

2. Tyczenie pośrednie prostych

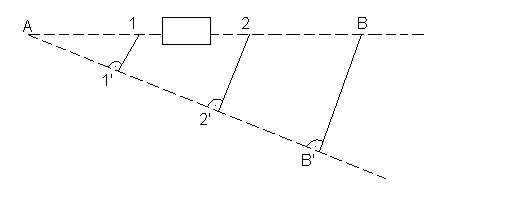
Tyczenie przez wąską przeszkodę

k = BB' : AB'= 11' : A1' = 22' : A2'

k = BB' * AB'

11' = k * A1'

22' = k * A2'

Sposoby tyczenia pośredniego wykorzystuje się wtedy, gdy nie można zastosować bezpośrednich metod np. gdy na boku AB jest przeszkoda, przesłaniająca wzajemną widoczność punktów końcowych odcinka. Pośrednie tyczenie prostej opiera się na pomiarze dostępnych elementów pewnej konstrukcji geometrycznej, a następnie obliczenie na tej podstawie miar wyznaczających lokalizację punktów pośrednich.

układ współrzędnych

Wyróżniamy m.in.:

• układ współrzędnych geograficznych (astronomiczny, geodezyjny)

• układ prostokątny (kartezjański) współrzędnych geocentrycznych

• układ współrzędnych biegunowych

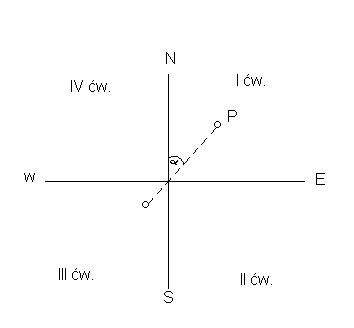
Układ współrzędnych geograficznych

Szerokość geograficzna φ jest to kąt zawarty pomiędzy kierunkami pionu (promieniem kuli) w danym punkcie P, a płaszczyzną równika.

Długość geograficzna jest to kąt dwuścienny zawarty pomiędzy płaszczyzną południka zerowego, a płaszczyzną południka przechodzącego przez punkt P.

W przypadku elipsoidy, zamiast kierunku pionu używamy pojęcia normalnej do elipsoidy w punkcie P, która z wyjątkiem położenia równikowego i biegunowego nie przechodzi przez środek Ziemi, odchylając się od kierunku siły ciężkości o pewien kąt. Elipsoidalne współrzędne graficzne B, L noszą nazwę współrzędnych geodezyjnych. Współrzędne te wraz z wysokością elipsoidalną h jednoznacznie określają pozycję dowolnego punktu na Ziemi.

Układ współrzędnych prostokątnych na płaszczyźnie

Układ matematyczny jest lewoskrętny, a geodezyjny prawoskrętny. Oznacza to, że kierunek liczenia kątów i ćwiartek w tym układzie jest zgodny z ruchem wskazówek zegara. Oś x skierowana jest na północ, a Y na wschód.

Położenie punktu wyrażamy za pomocą współrzędnych prostokątnych płaskich - X,Y, zaś orientację odcinka AB poprzez określenie jego azymutu A_AB, który jest kątem liczonym w prawo od północnej części płaszczyzny południka przechodzącego przez punkt.

Układ współrzędnych biegunowych

Układ ten tworzą:

• znany punkt B - początek układu współrzędnych

• wychodząca z niego półprosta zwana

osią bigunową

α

Rachunek współrzędnych

W rachunku współrzędnych wielkościami wyjściowymi lub szukanymi mogą być:

• elementy liniowe: współrzędne punktów x,y, przyrosty współrzędnych odcinków Δx, Δy, ich długości zredukowane

• elementy kątowe: azymuty, kąty kierunkowe

Przyrost współrzędnych - różnica pomiędzy współrzędną końca i współrzędną początku odcinka.

Azymut boku A_AB - jest to kąt kierunkowy zawarty pomiędzy kierunkiem północy, a dowolnym kierunkiem odcinka, mierzony zgodnie z ruchem wskazówek zegara.

Azymut odwrotny A_BA boku AB otrzymuje się przez dodanie 200^g do azymutu A_AB, gdy ten jest mniejszy od 200^g lub odjęcie 200^g, gdy jest większy od 200^g.

Czwartak φ - kąt ostry zawarty między kierunkiem odcinka, a najbliższa krawędzią osi x..

Podstawowe związki w układzie współrzędnych prostokątnych

Obliczanie przyrostów współrzędnych i współrzędnych punktów

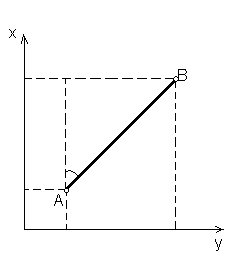
Podczas obliczenia przyrostu od współrzędnej

punktu B odejmuje się współrzędną punktu A.

Δx_AB = x_B - x_A x_B

Δy_AB = y_B - y_A

Jeżeli znany jest azymut boku AB i jego długość d_AB

pozioma d, wówczas przyrosty współrzędnych A_AB

oblicza się następująco:

x_A

Δx_AB = d_{AB *} cosA_AB

Δy_AB = d_{AB *} sinA_AB

y_A y_B

Znając przyrosty współrzędnych oraz współrzędne punktu A można obliczyć współrzędne punktu B.

x_B = x_A + cosA_AB

y_B = y_B + sinA_AB

Obliczenie azymutu i długości boku ze współrzędnych

1. Obliczenie przyrostów współrzędnych

2. Obliczenie czwartaka φ_AB ze wzoru:

φ_AB = arctg |Δy : Δx|

3. Ustalenie numeru ćwiartki i obliczenie azymutu boku

I ćwiartka - azymut = czwartak

II ćwiartka - azymut = 200^g - czwartak

III ćwiartka - azymut = 200^g + czwartak

IV ćwiartka - azymut = 400^g - czwartak

Ciąg poligonowy - wielobok otwarty lub zamknięty, w którym pomierzone zostały kąty wierzchołkowe i długości boków. Mogą one występować pojedynczo lub tworzyć sieci poligonowe. Ciągi poligonowe pod względem kształtu dzielą się na zamknięte i otwarte.

Bok nawiązania - odcinek zawarty pomiędzy punktem nawiązania danego ciągu, a najbliższym punktem poligonowym.

Kąt nawiązania - kąt mierzony na bliższym punkcie nawiązania, zaś drugie ramię, tzw. bok kierunkowy jest utworzony przez punkt nawiązania i sąsiedni punkt osnowy wyższej klasy lub rzędu w stosunku do danego ciągu poligonowego.

W ciągach poligonowych wyróżniamy kąty lewe i prawe.

Kąt lewy to kąt znajdujący się po lewej stronie ciągu w stosunku do poprzedniego boku ciągu.

Kąt prawy to kąt znajdujący się po prawej stronie ciągu w stosunku do poprzedniego boku ciągu.

Wyznaczenie azymutu boku następnego, gdy znany jest azymut boku poprzedniego i kąt pomiędzy bokami

A_n = A_p + α₁ - 200^g dla kątów lewych

A_n = A_p - β₁ + 200^g dla kątów prawych

Określenie azymutu ostatniego boku w ciągu

A_k = A_p + [α_p] - n _* 200^g dla kątów lewych

A_k = A_p - [β_p] + n _* 200^g dla kątów prawych

A_k - azymut boku końcowego

n - liczba kątów w ciągu

α_p, β_p - Suma kątów pomierzonych

A_p - azymut boku pierwszego

Rachunek wyrównawczy

Zajmuje się on:

• Wyrównywaniem obserwacji czyli uzgadnianiem wyników

• Analizami dokładności

• Wskazywaniem kierunku ulepszeń metod pomiaru, narzędzi geodezyjnych w celu otrzymania określonych dokładności

Błędy obserwacji geodezyjnych

Wyniki pomiarów geodezyjnych oznaczane symbolami l₁, l₂, l₃,…l_n nigdy nie są bezbłędne. Stanowią jedynie wartości przybliżone pewnych nieznanych wartości prawdziwych wielkości mierzonych.

X + ε = l X - wielkość prawdziwa

l - spostrzeżenie

ε - błąd prawdziwy

W czasie pomiaru popełniamy 3 grupy błędów:

• Błędy grube - mają duże wartości i są powodowane niestarannością, nieuwagą obserwatora itp. Są to błędy łatwo wykrywalne.

• Błędy systematyczne - powstają wskutek działania ustalonych prawidłowości określonych w warunkach pomiaru

• Błędy przypadkowe - mają charakter losowy i są błędami niezależnymi od obserwatora. Tymi błędami zajmuje się rachunek wyrównawczy. Błędy te spowodowane są niedokładnością ludzkich zmysłów, narzędzi, warunkami pomiaru. Są błędami narastającymi, sumującymi się w kwadratach.

ε

Gauss ustalił funkcyjne zależności między wielkościami błędów przypadkowych a prawdopodobieństwem ich pojawienia się:

φ(ε) = √ Π * e

φ(ε) - funkcja określająca szybkość zmiany prawdopodobieństwa pojawienia się błędu ε

ε - przypadkowy prawdziwy błąd spostrzeżenia

h - parametr zależny od dokładności wykonania spostrzeżenia

e = 2,718281828

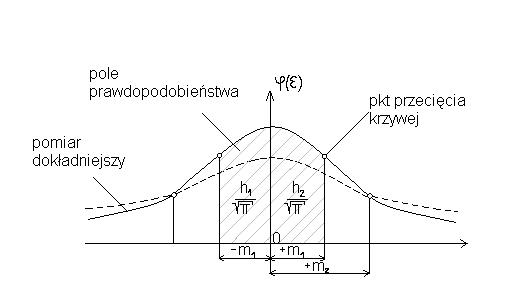
Z przebiegu krzywej prawdopodobieństwa wysuwamy pewne wnioski o właściwościach błędów przypadkowych:

1. Prawdopodobieństwo pojawienia się błędów ujemnych i dodatnich o tej samej wartości bezwzględnej jest jednakowe

2. Prawdopodobieństwo pojawienia się błędu o mniejszej wartości bezwzględnej jest większe niż prawdopodobieństwo błędu o większej wartości bezwzględnej

3. Najbardziej prawdopodobne jest pojawienie się błędu przypadkowego równego zero.

4. Prawdopodobieństwo pojawienia się mniejszych błędów przypadkowych rośnie szybciej dla tego szeregu spostrzeżeń, który wyk. przy użyciu bardziej precyzyjnych metod i narzędzi.

Ocena błędów spostrzeżeń

W warunkach geodezyjnych do oceny dokładności spostrzeżeń stosowane są różne miary dokładności.

1. Błąd średni wśród zbioru błędów szeregu spostrzeżeń przy ilości spostrzeżeń to taki błąd, którego kwadrat jest średnią arytmetyczną kwadratu błędów tego zbioru.

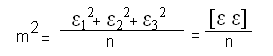
2. Błąd graniczny zawiera się między 2m<g<4m

3. Błąd przeciętny jest błędem będącym średnią arytmetyczną z bezwzględnych wartości szeregu błędów prawdziwych danej wielkości.

4. Błąd względny - stosunek bezwzględnej wartości błędu najczęściej średniego do wartości mierzonej

W =

Wagi spostrzeżeń

Wagi spostrzeżeń to współczynniki określające stopień zaufania do pomiaru. Im większa waga tym większa dokładność pomiaru.

Sposoby określania wag spostrzeżeń:

1. 
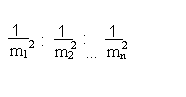
   Jeżeli znane są błędy średnie spostrzeżeń to wagi są odwrotnie proporcjonalne do kwadratu tych błędów.

p₁ : p₂ : … : p_n =

2. Jeżeli pomierzono bezpośrednio grupę wielkości w jednakowych warunkach pomiarów, lecz każdą z nich niejednakową ilość razy to wagi spostrzeżeń są wprost proporcjonalne do liczby dokonywanych pomiarów.

p₁ : p₂ : …: p_n = n₁ : n₂ : … : n_n

3. Jeżeli wielkości podlegające pomiarowi składają się z różnej ilości elementów składowych pomierzonych z jednakową dokładnością każdy, to wagi spostrzeżeń są odwrotnie proporcjonalne do liczby elementów składowych lub do wielkości proporcjonalnej do tej liczby.

p₁ : p₂ : … : p_n =

Prawo przenoszenia się błędów średnich

Prawo przenoszenia się błędów średnich umożliwia ocenę dokładności funkcji, jeżeli znana jest dokładność spostrzeżeń i ich funkcji. Służy do określenia dokładności funkcji, jeżeli znana jest dokładność spostrzeżeń lub do obliczania dokładności wykonywanych pomiarów w celu osiągnięcia założonej dokładności efektu końcowego określonego na podstawie tych pomiarów.

m²_φ = f_x² * m_x² + f_y² * m_y² + f_z² * m_z²

m_φ - błąd średni funkcji spostrzeżeń

m_x, m_y, m_z - błędy średnie spostrzeżeń x, y, z

f_x, f_y, f_z - pochodne cząstkowe funkcji względem zmiennych x, y, z po podstawieniu do nich wartości przybliżonych

---