Szkolny Konkurs Matematyczny

Zadania dla klas pierwszych

Luty 2011

Zadanie 1

(5 pkt.) Na konkursie matematycznym uczeń miał do rozwiązania 10 zadań. Ustalono następującą punktację: za każde dobrze rozwiązane zadanie uczeń otrzymywał 5 punktów, a za źle rozwiązane zadanie tracił 3 punkty. Ile zadań zostało rozwiązanych dobrze, jeśli uczeń otrzymał:

a) 34 punkty b) 10 punktów.

Zadanie 2

(5 pkt.) Różnica dwóch liczb wynosi 60.Znajdź te liczby, jeżeli wiadomo, że 60% pierwszej z nich wynosi tyle co 150% drugiej liczby.

Zadanie 3

(5 pkt.) Siostra jest o 3 lata młodsza od brata. Brat ma obecnie 2 razy tyle lat, ile siostra miała wtedy, kiedy brat miał tyle lat ile siostra ma teraz. Ile lat ma siostra, a ile brat?

Zadanie 4

(5 pkt.) Obwód przedniego koła wynosi 35
, a tylnego 44
. Na drodze
prze-dnie koło wykonało o 387 obrotów więcej niż tylne. Oblicz
.

Zadanie 5

( 5 pkt.) Z trójkąta równobocznego o długości boku 12 cm wycięto koło wpisane w ten trójkąt. Oblicz pole powierzchni i obwód tego koła.

Zadanie 6

(5 pkt.) Krzyś wypił
szklanki soku i dolał wody. Następnie wypił
szklanki wody
z sokiem i dodał wody. Potem wypił
szklanki wody z sokiem i znów dolał wody.
W końcu wypił całą szklankę wody z sokiem. Czego wypił więcej, wody czy soku i o ile? Odpowiedź uzasadnij.

Zadanie 7

(3 pkt.) Marynarze mierzą kąty za pomocą jednostki kątowej zwanej rumbem. Rumb to kąt środkowy oparty na
okręgu. Ile stopni ma jeden rumb, a ile rumbów ma kąt prosty.

POWODZENIA !

OSTATECZNY TERMIN SKŁADANIA ROZWIĄZAŃ: 28 luty 2011

Szkolny Konkurs Matematyczny

Zadania dla klas drugich

Luty 2011

Zadanie 1

(5 pkt. Cena wynajęcia autokaru na wycieczkę wynosi 1200 zł. Gdyby 4 uczniów tej klasy zrezygnowało z wycieczki, to każdy z pozostałych płaciłby o 10 zł więcej. Ilu uczniów liczy ta klasa?

Zadanie 2

(5 pkt.) Oblicz wartość wyrażenia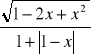
dla

Zadanie 3

(5 pkt.) Z trzech trójkątów równobocznych zbudowano trapez o polu

. Oblicz obwód trapezu i długość jego przekątnych. Uzasadnij, że na trapezie można opisać okrąg. Oblicz promień tego okręgu.

Zadanie 4

( 5 pkt.) Suma trzech liczb naturalnych jest równa 210. Jakie to liczby jeśli wiadomo, że druga liczba stanowi
pierwszej, a trzecia jest średnią arytmetyczną pierwszej i drugiej.

Zadanie 5

(3 pkt.) Dziecko zjeżdża na sankach ze stoku. W pierwszej sekundzie sanki przebyły drogę 2
, a w każdej następnej sekundzie o 0,4
więcej niż w poprzedniej. Jaką drogę przebyły sanki po 15 sekundach.

Zadanie 6

(4 pkt.) Dana jest funkcja kwadratowa określona wzorem
. Rozwiąż nierówność
. Ze zbioru rozwiązań nierówności
wypisz wszystkie liczby naturalne.

Zadanie 7

(6 pkt.) Jan przygotowuje się do turnieju „Wiem wszystko”. Ma do rozwiązania 3000 zadań. Rozwiązał już 200 z nich. Dzisiaj rozwiązał 10 zadań teraz codziennie będzie rozwiązywał o 5 zadań więcej. Ile dni zajmie Janowi rozwiązanie wszystkich pozostałych zadań.

POWODZENIA !

OSTATECZNY TERMIN SKŁADANIA ROZWIĄZAŃ: 28 luty 2011

Szkolny Konkurs Matematyczny

Zadania dla klas trzecich i czwartych

Luty 2011

Zadanie 1

(5 pkt.) Pewien kierowca kupuje regularnie benzynę za 180 zl . Po podwyżce ceny benzyny o 15 groszy za litr stwierdził, ze otrzymał o 2 litry benzyny mniej niż zwykle. Oblicz cenę 1 litra benzyny po podwyżce.

Zadnie 2

(5 pkt.) Uzasadnij, ze tylko jeden wyraz ciągu o wyrazie ogólnym
jest większy od 40.

Zadanie 3

(4 pkt.) Przekrój osiowy stożka jest trójkątem o polu

i kacie przy podstawie
. Oblicz objętość i pole powierzchni całkowitej stożka.

Zadanie 4

(6 pkt.) Prostokątny kawałek papieru o powierzchni 180
zwinięto w rulon na dwa sposoby tak, że w każdym przypadku tworzy powierzchnię boczną walca. Wiedząc, że objętość jednego walca jest 5 razy mniejsza od objętości drugiego walca , oblicz:

1. wymiary prostokątnego kawałka papieru;

2. objętość każdego z tych walców.

Zadanie 5

(3 pkt.) W ćwiartkę koła wpisano kwadrat. Oblicz stosunek pola kwadratu do pola wycinka koła.

Zadanie 6

(5 pkt.) Dana jest funkcja określona wzorem
. Sporządź wykres funkcji. Oblicz współrzędne punktów, w których wykres funkcji przecina osie układu współrzędnych.

Zadanie 7

(5 pkt.) Znajdź liczbę dwucyfrową , wiedząc, ze różnica jej cyfr jest równa 3, iloczyn tej liczby przez sumę jej cyfr jest równy 324.

POWODZENIA !

OSTATECZNY TERMIN SKŁADANIA ROZWIĄZAŃ:

28 luty 2011

---