ĆWICZENIE PROJEKTOWE NUMER 1. |
|
|
|||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1.1 Wyznaczyć parametry (wartość średnia, odchylenie standardowe, współczynnik zmienności losowych cech geometrycznych przekroju płaskownika stalowego (szerokość b(ω) i grubość t(ω) na podstawie pomiarów, tablica 1 ((bi) t(i)) |
|
|
|||||||||
|
|
|
|||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tablica 1 |
|
|
|
|
|
|
|
|
|
|
|
b(ω) |
t(ω) |
bi-bśr |
(bi-bśr)2 |
ti-tśr |
(ti-tśr)2 |
(bi-bśr)(ti-tśr) |
|
|
|
|
|
91,1936 |
15,6348 |
3,41677 |
11,67432 |
-0,358 |
0,1280 |
-1,22252 |
|
|
|
|
|
86,6876 |
15,5702 |
-1,08923 |
1,186422 |
-0,422 |
0,1784 |
0,46009 |
|
|
|
|
|
86,2879 |
15,9569 |
-1,48893 |
2,216913 |
-0,036 |
0,0013 |
0,05315 |
|
|
|
|
|
93,2523 |
16,2801 |
5,47547 |
29,98077 |
0,288 |
0,0827 |
1,57420 |
|
|
|
|
|
82,9681 |
16,7526 |
-4,80873 |
23,12388 |
0,760 |
0,5776 |
-3,65463 |
|
|
|
|
|
88,2194 |
16,2081 |
0,44257 |
0,195868 |
0,216 |
0,0464 |
0,09537 |
|
|
|
|
|
90,2794 |
16,0471 |
2,50257 |
6,262857 |
0,055 |
0,0030 |
0,13639 |
|
|
|
|
|
82,3006 |
15,6673 |
-5,47623 |
29,9891 |
-0,325 |
0,1058 |
1,78142 |
|
|
|
|
|
85,3053 |
15,751 |
-2,47153 |
6,108461 |
-0,242 |
0,0584 |
0,59712 |
|
|
|
|
|
91,2741 |
16,0579 |
3,49727 |
12,2309 |
0,065 |
0,0043 |
0,22837 |
|
|
|
|
suma: |
877,7683 |
159,926 |
0,00 |
122,97 |
0,00 |
1,19 |
0,04896 |
|
|
|
|
n- ilość pomiarów |
|
|
|
|
|
|
|
||
|
|
n= |
10 |
|
|
|
|
|
|
|
|
Obliczenia przeprowadzone dla wyników pomierzonych szerokości: |
|
|
|||||||||
a) wartość średnia pomierzonych szerokości b(ω): |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
b,śr= |
87,77683 |
[mm] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b) odchylenie standardowe sx: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
sb= |
3,70 |
[mm] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c) współczynnik zmienności ν: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νb= |
0,0421 |
|
|
|
|
|
|
|
|
|
|
νb[%]= |
4,21 |
[%] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Obliczenia przeprowadzone dla wyników pomierzonych grubości: |
|
|
|||||||||
d) wartość średnia pomierzonych grubości t(ω): |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
t,śr= |
15,99 |
[mm] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b) odchylenie standardowe sx: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
st= |
0,36 |
[mm] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c) współczynnik zmienności ν: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νt= |
0,0227 |
|
|
|
|
|
|
|
|
|
|
νt[%]= |
2,27 |
[%] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2 Wyznaczyć parametry losowej wytrzymałości stali w(ω) na podstawie pomiarów w próbie rozciągania- tablica 2 |
|
|
|||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tablica 2 |
|
|
|
|
|
|
|
|
|
|
|
w(i) [Mpa] |
w(i)-wśr |
(wi-wśr)2 |
|
|
|
|
|
|
|
|
|
437,467 |
3,449 |
11,896 |
|
|
|
|
|
|
|
|
|
457,208 |
23,190 |
537,776 |
|
|
|
|
|
|
|
|
|
408,364 |
-25,654 |
658,128 |
|
|
|
|
|
|
|
|
|
457,969 |
23,951 |
573,650 |
|
|
|
|
|
|
|
|
|
450,898 |
16,880 |
284,934 |
|
|
|
|
|
|
|
|
|
456,319 |
22,301 |
497,335 |
|
|
|
|
|
|
|
|
|
456,708 |
22,690 |
514,836 |
|
|
|
|
|
|
|
|
|
437,832 |
3,814 |
14,547 |
|
|
|
|
|
|
|
|
|
426,015 |
-8,003 |
64,048 |
|
|
|
|
|
|
|
|
|
400,749 |
-33,269 |
1106,826 |
|
|
|
|
|
|
|
|
|
450,512 |
16,494 |
272,052 |
|
|
|
|
|
|
|
|
|
460,477 |
26,459 |
700,079 |
|
|
|
|
|
|
|
|
|
396,801 |
-37,217 |
1385,105 |
|
|
|
|
|
|
|
|
|
411,492 |
-22,526 |
507,421 |
|
|
|
|
|
|
|
|
|
401,459 |
-32,559 |
1060,088 |
|
|
|
|
|
|
|
|
suma: |
6510,270 |
0,000 |
8188,721 |
|
|
|
|
|
|
|
|
n- ilość pomiarów |
|
|
|
|
|
|
|
||
|
|
n= |
15 |
|
|
|
|
|
|
|
|
Obliczenia przeprowadzone dla wyników pomierzonych wytrzymałości: |
|
|
|||||||||
a) wartość średnia : |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
w,śr= |
434,02 |
[MPa] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b) odchylenie standardowe sx: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
sw= |
24,18 |
[MPa] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c) współczynnik zmienności ν: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νw= |
0,0557 |
|
|
|
|
|
|
|
|
|
|
νw[%]= |
5,57 |
[%] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2 Wyznaczyć parametry losowej siły rociągającej P(ω) na podstawie pomiarów w próbie rozciągania- tablica 3 |
|
|
|||||||||
|
|
|
|||||||||
|
|
|
Tablica 3 |
|
|
|
|
|
|
|
|
|
|
|
P(i) [kN] |
P(i)-Pśr |
(Pi-Pśr)2 |
|
|
|
|
|
|
|
|
|
451,639 |
3,81 |
14,53 |
|
|
|
|
|
|
|
|
|
483,391 |
35,56 |
1264,74 |
|
|
|
|
|
|
|
|
|
412,785 |
-35,04 |
1228,00 |
|
|
|
|
|
|
|
|
|
466,441 |
18,61 |
346,45 |
|
|
|
|
|
|
|
|
|
366,102 |
-81,73 |
6679,11 |
|
|
|
|
|
|
|
|
|
451,689 |
3,86 |
14,91 |
|
|
|
|
|
|
|
|
|
487,641 |
39,81 |
1585,09 |
|
|
|
|
|
|
|
|
|
457,485 |
9,66 |
93,26 |
|
|
|
|
|
|
|
|
|
445,617 |
-2,21 |
4,89 |
|
|
|
|
|
|
|
|
|
477,879 |
30,05 |
903,07 |
|
|
|
|
|
|
|
|
|
442,275 |
-5,55 |
30,83 |
|
|
|
|
|
|
|
|
|
405,944 |
-41,88 |
1754,25 |
|
|
|
|
|
|
|
|
|
470,706 |
22,88 |
523,41 |
|
|
|
|
|
|
|
|
|
492,504 |
44,68 |
1995,96 |
|
|
|
|
|
|
|
|
|
405,319 |
-42,51 |
1807,00 |
|
|
|
|
|
|
|
|
suma: |
6717,417 |
0,000 |
18245,505 |
|
|
|
|
|
|
|
|
n- ilość pomiarów |
|
|
|
|
|
|
|
||
|
|
n= |
15 |
|
|
|
|
|
|
|
|
Obliczenia przeprowadzone dla wyników pomierzonych sił rozciągających: |
|
|
|||||||||
a) wartość średnia : |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
P,śr= |
447,83 |
[kN] |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
b) odchylenie standardowe sx: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
sP= |
36,10 |
[kN] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c) współczynnik zmienności ν: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νP= |
0,0806 |
|
|
|
|
|
|
|
|
|
|
νP[%]= |
8,06 |
[%] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.1 Wyznaczyć współczynnik korelacji liniowej pomiędzy b(ω) i t(ω) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
a) współczynnik korelacji liniowej: |
|
|
|
|
|
|
|
||||
|
|
|
x |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
ρbl € <-1;1> |
|
|
|
|
|||||
|
|
ρbl= |
0,0041 |
więc zmienne nie są skorelowane |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2.2 Aproksymacja za pomocą rozkładu normalnego parametrów losowych pola przekroju płaskownika A(ω) |
|
|
|||||||||
|
|
|
|||||||||
|
|
z(ω)=b(ω)*t(ω) |
|
|
|
|
|
|
|
||
|
|
zśr=bśr*tśr |
|
|
|
xśr=87,77683[mm] |
|
|
|
||
|
|
Aśr=87,7768*15,99= |
1403,78 |
[mm2] |
|
sy=0,36[mm] |
|
|
|
||
|
|
|
sx=3,70[mm] |
|
|
|
|||||
|
|
|
yśr=15,99[mm] |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
sA=Sz= |
67,17 |
[mm2] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vx=0.0421 |
|
|
|
|
|
|
|
|
|
|
|
vy=0,0227 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νA=Vz= |
0,0478 |
|
|
|
|
|
|
|
|
|
|
νA[%]= |
4,78 |
[%] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.3 Wyznaczenie obliczeniowego pola przekroju Ao,tak aby prawdopodobieństwo |
|
|
|
||||||||
wystapienia przekroju mniejszego niż Ao nie przekroczyło: |
|
|
|
|
|
||||||
|
|
a= |
69 |
|
tab.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
0,05 |
ai= |
0,0569 |
|
|
|
|
|
|
|
|
|
bezpieczeństwo: |
|
|
|
|
|
|
|
|
||
|
|
B=1-0,0569 |
|
|
|
|
|
|
|
|
|
|
|
B= |
0,9431 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,94295 |
0,9431 |
94408 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
1,58 |
|
1,59 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x= |
1,5889E-11 |
|
|
|
|
|
|
|
|
|
|
t= |
1,58000 |
|
|
|
|
|
|
|
|
|
|
Aśr=1403,78 |
|
|
|
|
|
|
|
|
|
|
|
Ao=Aśr-t*sA |
|
|
615,7301 |
|
|
|
|
|
|
|
|
Ao= |
1297,65 |
[mm2] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b) |
0,01 |
ai= |
0,0169 |
|
|
|
|
|
|
|
|
|
bezpieczeństwo: |
|
|
|
|
|
|
|
|
||
|
|
B=1-0,0169 |
|
|
|
|
|
|
|
|
|
|
|
B= |
0,9831 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,983 |
0,9831 |
0,98341 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
2,15 |
|
2,16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x= |
0,00243902 |
|
|
|
|
|
|
|
|
|
|
t= |
2,15244 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ao=Aśr-t*sA |
|
|
599,7085 |
|
|
|
|
|
|
|
|
Ao= |
1259,20 |
[mm2] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c) |
0,0013 |
ai= |
0,001369 |
|
|
|
|
|
|
|
|
|
bezpieczeństwo: |
|
|
|
|
|
|
|
|
||
|
|
B=1-0,001369 |
|
|
|
|
|
|
|
||
|
|
B= |
0,998631 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,998605 |
0,998631 |
0,99865 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
2,99 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x= |
0,00577778 |
|
|
|
|
|
|
|
|
|
|
t= |
2,99578 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ao=Aśr-t*sA |
|
|
|
|
|
|
|
|
|
|
|
Ao= |
1202,56 |
[mm2] |
575,6761 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pole nominalne: |
|
|
|
|
|
|
|
||
|
|
An=bn*tn |
|
bn= |
85 |
tn= |
16 |
|
|
|
|
|
|
An= |
1360 |
[mm2] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.4 Wyznaczyć parametry losowego wskaźnika wytrzymałości przy zginaniu Wx(ω) przekroju płaskownika |
|
|
|||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bśr= |
87,77683 |
|
sb= |
3,70 |
|
|
|
|
|
|
|
tśr= |
15,99 |
|
st= |
0,36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wx=1/6*tśr*(bśr)2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wx= |
20536,556 |
[mm3] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
14,6294717 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
467,926577 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sWx= |
1791,34493 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νWx=sWx/Wx |
|
|
|
|
|
|
|
|
|
|
|
νWx= |
0,0872 |
|
|
|
|
|
|
|
|
|
|
νWx[%]= |
8,72 |
[%] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Parametry losowego momentu bezwładności przy zginaniu Ix(ω) przekroju przy zginaniu |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ix=(tśr*bśr3)/12 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ix= |
901316,88 |
[mm4] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sIx= |
115689,685 |
[mm^4] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νIx= |
0,1284 |
|
|
|
|
|
|
|
|
|
|
νIx[%]= |
12,84 |
[%] |
|
|
|
|
|
|
|
Porównanie wyników współczynnika zmienności: |
|
|
|
|
|
|
|||||
|
|
νb= |
4,21 |
[%] |
|
|
|
|
|
|
|
|
|
νt= |
2,2697 |
[%] |
|
|
|||||
|
|
νA= |
4,7848 |
[%] |
|
|
|
|
|
|
|
|
|
νWx= |
8,72 |
[%] |
|
|
|
|
|
|
|
|
|
νIx= |
12,84 |
[%] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.1 Wyznaczyć parametry losowej nośności na rozciąganie Nrt(ω) płaskownika stalowego o losowym przekroju(A(ω), zad.2.2) oraz losowej wytrzymałości stali w(ω) |
|||||||||||
|
|||||||||||
|
|
|
|
Nrt,śr+t*Sn |
|
|
|
|
|
|
|
|
|
|
|
Nrt,śr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nrt,śr-t*Sn |
|
t-indeks niezawodności Cornella(ufności) |
|
||||
|
|
|
|
|
|
(obiektywna miara bezpieczeństwa elementu) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ścieżka rownowagi pręta rozciąganego. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nrt(ω)=A(ω)*W(ω)-losowa nośność pręta rozciąganego osiowo |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nrt,śr=Aśr*Wśr-wartość średnia losowej nośności |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aśr= |
0,00140378 |
[m2] |
|
|
|
|
|
|
|
|
|
Wśr= |
434018,00 |
[kN/m2] (z pkt.1.2) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nrt,śr= |
609,27 |
[kN] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sA= |
0,00006717 |
[m2] (pkt.2.2) |
|
|
|
|
|
||
|
|
sw= |
24184,88 |
[kN/m2] (z pkt.1.2) |
|
|
|
|
|
||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
|
sNrt= |
44,78 |
[kN] -odchylenie standardowe(Sn) losowej nośności |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
P,śr=447,83[kN] |
|
|
|
|
|
|||
|
|
|
Sp=36,1[kN] (pkt.1.2) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
t= |
2,81 |
|
t*Sn= |
125,6805 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N+t*sN= |
734,95 |
[kN] |
|
|
|
|
|
|
|
|
|
N-t*sN= |
483,59 |
[kN] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.2 Oszacować bezpieczeństwo płaskownika stalowego (wg zad. 3.1) obciążonego osiowo losową siłą rozciągającą P(ω) o parametrach wg zadania 1.3 |
|||||||||||
|
|||||||||||
|
|
Nrt,śr=609,27[kN] |
sNrt= |
44,78[kN] -parametry losowe nośności |
|
|
|||||
|
|
P,śr=447,83[kN] |
Sp=36,1[kN] -parametry osiowego obciążenia |
|
|
|
|||||
|
|
Wartość dystrybuanty: |
|
|
|
|
|
|
|
||
|
|
F(t)=F(2,81)= |
0,997523 |
|
odczt. Tab 3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Niezawodność : |
|
|
|
|
|
|
|
||
|
|
R= |
0,997523 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Awaryjność: |
|
|
|
|
|
|
|
||
|
|
A=1-R |
|
|
|
|
|
|
|
|
|
|
|
A= |
0,002477 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3 Wyznaczyć parametry losowej siły rociągającej P1(ω), aby bezpieczeństwo stalowego płaskownika z zad. 3.2 wyniosłoR= 0,999a zakładając ten sam (jak w zad. 3.2) wsp. zmienności siły osiowej. |
|||||||||||
|
|||||||||||
|
|
|
Dla R=0,99969 |
|
|
|
|
|
|
||
|
|
ν=sP/Pśr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νP= |
0,0806 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Parametr t rozkładu normalnego dla dystrybuanty R=F(t)=0,99969 wynosi: |
|
|
|
||||||
|
|
t= |
3,43 |
odczt. Tab 3 |
|
|
|
|
|
||
|
|
|
Dane: |
Nrt,śr=609,27[kN] |
|
|
|
||||
|
|
=> |
|
t=3,43 |
|
|
|
|
|||
|
|
|
|
vp=0,0806 |
|
|
|
|
|||
|
|
|
|
sNrt=44,78 |
[kN] |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(+)1śr= |
417,18 |
[kN]-losowa siła rozciągająca(zapas nośności jest większy) |
|
||||||
|
|
P(-)1śr= |
902,22 |
[kN]-"odpada" |
|
|
|
|
|
||
|
|
przy sile P1=417,18[kN] zapas nośności jest większy |
|
|
|
|
|||||
|
|
sP1,śr=νP1,śr*P1,śr |
|
|
P(+)1śr/Nrt,śr=417,18/609,72=0,68 |
|
|||||
|
|
sP1,śr=0,0806*417,18= |
33,63 |
[kN] |
|
więc zapas nosności wynosi 31% |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sprawdzenie: |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t= |
3,43 |
ok. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.1 Dany jest łańcuch złożony z 57 elementó (ogniw). Ogniwa wykonano z płaskownika o losowej nośności (wg zad. 3.3). |
|||||||||||
Oszacować: |
n= |
57 |
|
|
|
|
|
|
|
||
a) Obliczeniową nosność graniczną pojedyńczego ogniwa dla bezpieczeństwa pi=0,999a |
|
|
|||||||||
|
|
a= |
69 |
|
Dane: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi= |
0,99969 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9996869 |
0,99969 |
0,9996982 |
|
0,000011 |
0,000003 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
3,42 |
|
3,43 |
|
0,01 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x= |
0,00274336 |
|
|
|
|
|
|
|
|
|
|
t= |
3,42 |
|
|
|
|
|
|
|
|
|
|
dane:(parametry losowe nośności) |
|
|
|
|
|
|
|||
|
|
Nrt,śr= |
609,27 |
[kN] |
|
|
|
|
|
|
|
|
|
sNrt= |
44,78 |
[kN] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Obliczeniowa nośność graniczna dla jednego ogniwa: |
|
|
|
|
|||||
|
|
Noi=Ni,śr-t*sNi |
|
|
|
|
|
|
|
||
|
|
Noi= |
456,00 |
[kN] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b) bezpieczeństwo łańcucha rozciąganego siłą P2(ω) o parametrach: |
|
|
|
|
|||||||
|
|
|
|
|
|
Dane:(parametry losowe obciążenia) |
|
||||
|
|
P2śr=1,1*P1śr |
|
|
|
P1śr= |
417,18 |
[kN] |
|
||
|
|
P2śr= |
458,90 |
[kN] |
|
|
sP1,śr= |
33,63 |
[kN] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sP2,śr= |
1,1*sP1,śr |
|
|
|
|
|
|
|
|
|
|
sP2,śr= |
36,99 |
[kN] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
indeks niezawodności pojedyńczego ogniwa |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t= |
2,59 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bezpieczeństwo jednego ogniwa: |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi=F(2,59) |
|
|
|
|
|
|
|
|
|
|
|
pi= |
0,995201 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bezpieczeństwo łańcucha złożonego z 57 ogniw: |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R= |
0,7601789 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c) obliczeniową nośność graniczną łańcucha dla bezpieczeństwa Ro=0,999a |
|
|
|
|
|||||||
|
|
a= |
69 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ro= |
0,99969 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
pi= |
0,99999456 |
|
|
|
|
|
|
|
|
Aby bezp.łancucha o n=57 wyniosło |
Ro=0,99969, bezp.1 ogniwa musi wynosić pi=0,99999456 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,99999433 |
0,99999456 |
0,99999459 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
4,39 |
|
4,4 |
|
0,01 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x= |
0,00896373 |
|
|
|
|
|
|
|
|
|
|
t= |
4,39896 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Obliczeniowa nośność graniczna łańcucha dla Ro=0,99969 wynosi: |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
No=NRt,śr-t*sNrt |
|
Nrt,śr= |
609,27 |
[kN] |
|
|
|
||
|
|
No= |
412,29 |
[kN] |
sNrt= |
44,78 |
[kN] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d) efekt statystycznego osłabienia systemu |
|
|
|
|
|
|
|
||||
|
|
Dane: |
Noi= |
456,00 |
[kN] |
|
|
|
|
|
|
|
|
νo=No/Noi |
|
|
|
|
|
|
|
|
|
|
|
νo= |
0,9041 |
|
|
|
|
|
|
|
|
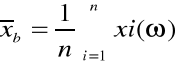
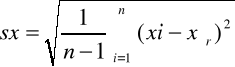
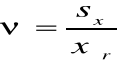
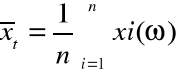
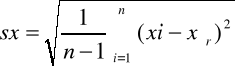
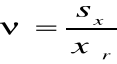
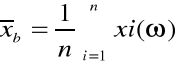
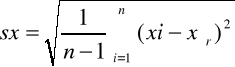
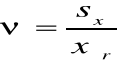
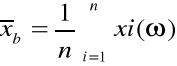
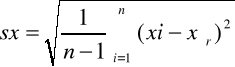
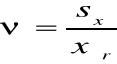
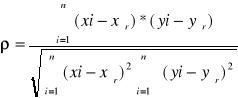
![]()
![]()
![]()
![]()
![]()
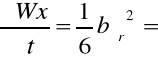
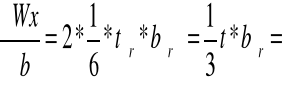
![]()
![]()
![]()
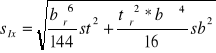
![]()
![]()
![]()
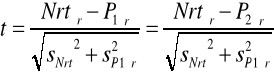
![]()
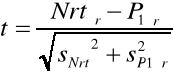
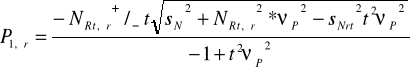
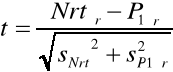
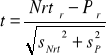
![]()
Wyszukiwarka
Podobne podstrony:
BEZPIECZEŃSTWO I NIEZAWODNOŚĆ KONSTRUKCJI
1 2 Dystrybuanta, Niezawodność konstr, niezawodność, 1 projekt
08 Paczkowska T i inni Bledy projektanta zagrozeniem bezpieczenstwa stalowej konstrukcji dachu
Probabilistyczna ocena niezawodności konstrukcji metodami Monte Carlo z wykorzystaniem SSN
Zadanie 01 statystyka, Niezawodność konstr, niezawodność, 1 projekt
Zadanie 10 uklady, Niezawodność konstr, niezawodność
niezawodność konstrukcji
bpb SU 4 BEZPIECZEŃSTWO BUDYKKÓW konstrukcje
Zadanie 06 Hasofer-Lind, Niezawodność konstr, niezawodność, 2 projekt
Projekt SEMESTRALNY NIEZAWODNOŚĆ, Niezawodność konstr, niezawodność
Wyklad IV Zadania, Niezawodność konstr, niezawodność
Zadanie 08 Turkstra, Niezawodność konstr, niezawodność, Niezawodność konstrukcji, 3-Normy projektowe
Bezpieczeństwo energetyczne - Bojarski, Energetyka Politechnika Krakowska Wydział Mechaniczny I stop
Zadanie 07 Rackwitz-Fiessler, Niezawodność konstr, niezawodność, 2 projekt
Projekt semestralny, Niezawodność konstr, niezawodność, niezawodnośc, projekt pika
Zadanie 09 kalibracja, Niezawodność konstr, niezawodność, Niezawodność konstrukcji, 3-Normy projekto
Wyklad I Zadania, Niezawodność konstr, niezawodność
więcej podobnych podstron