W Y K Ł A D 10

MOCE DLA PRZEBIEGÓW SINUSOIDALNYCH I WARUNKI DOPASOWANIA ODBIORNIKA DO ŹRÓDŁA NAPIĘCIA SINUSOIDALNEGO

10.1. Moce dla przebiegów sinusoidalnych i ich zachowawczość

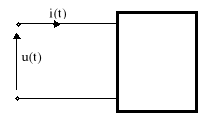
Dla dwójnika liniowego przedstawionego na rys.10.1 opisanego parą przebiegów sinusoidalnych u(t), i(t)

u(t) = 
 |U| sin(ωt + α), (10.1)

i(t) = 
 |I| sin(ωt +β), (10.2)

definiuje się następujące moce:

Rys.10.1. Dwójnik liniowy

• moc chwilową

p(t) = u(t) i(t) = |U| |I| cosϕ - |U| |I| cos(2ωt + 2α - ϕ), (10.3)

• moc czynną

P =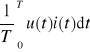
= |U| |I| cosϕ, (10.4)

• gdzie: ϕ = α − β ,

• moc bierną Q = |U| |I| sinϕ, (10.5)
  

• moc pozorną |S| = |U| |I| =
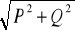
  , (10.6)
  

• moc symboliczną S = P + jQ = U I^* (10.7)
  

gdzie: I^* - wartość skuteczna zespolona sprzężona prądu.

Oprócz przedstawionych mocy, w elektrotechnice wprowadza się wielkość, zwaną współczynnikiem mocy źródła

. (10.8)

Z wymienionych mocy, zachowawczymi są: moc chwilowa, moc czynna, moc bierna, moc symboliczna, tzn. te moce podlegają bilansowi mocy. Natomiast nie jest zachowawcza moc pozorna |S|.

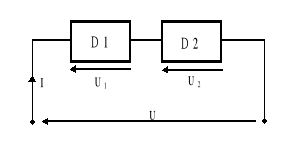
Rys.10.2. Dwa dwójniki liniowe połączone szeregowo

. (10.9)
Natomiast całkowita moc symboliczna obydwu dwójników

S = U I^* = (U₁+U₂) I^*= U₁ I^* + U₂ I^*= S₁ + S₂, (10.10)
S = P + jQ = P₁ + P₂ + j(Q₁+Q₂), (10.11)

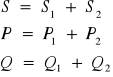
. (10.12)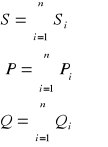

. (10.13)

Moce pozorne dla poszczególnych dwójników

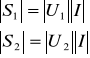
. (10.14)
Natomiast moc pozorna całego układu

|S| = |U| |I| = |U₁+U₂| |I|. (10.15)
Ponieważ

|U₁ + U₂| ≤ |U₁| + |U₂| , (10.16)
więc

|S| ≤ |S₁| + |S₂| . (10.17)

Ze związku (10.17) wynika, że moc pozorna nie jest mocą zachowawczą. Dla układów o dowolnej konfiguracji zachodzi związek

. (10.18)

10.2. Znaczenie techniczne współczynnika mocy i jego poprawa

Współczynnik mocy źródła określony zależnością

≤ 1 (10.19)

określa, jaką część mocy pozornej |S| pobieranej przez różne urządzenia elektryczne stanowi moc czynna P. Wskazuje zatem na wykorzystanie mocy |S| dostarczonej ze źródła do odbiornika.

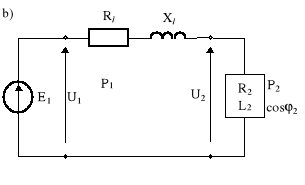
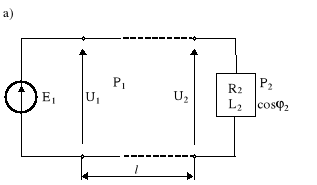
Rys.10.3. Układ: a) źródło - linia transmisyjna - odbiornik; b) schemat zastępczy

Rezystancja przewodów linii określona jest za pomocą zależności

R_l = 2R_p = 2
, (10.20)
natomiast indukcyjność własna linii napowietrznej dwuprzewodowej

L_l = 
, (10.21)
gdzie:

ρ - rezystywność materiału (przewodów) s - przekrój przewodu,

l - długość linii,  d - odstęp między przewodami,  r - promień przekroju przewodu.

Moc czynna odbiornika wyraża się zależnością

P₂ = |U₂| |I| cosϕ₂, (10.22)

. (10.23)
ΔP_l = R_l | I |² =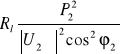
. (10.24)
ΔQ_l = X_l | I |² = X_l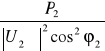
. (10.25)

Straty te powodują zapotrzebowanie na większą moc czynną P₁ wydawaną przez źródło, moc bierną i pozorną zgodnie z zależnościami

P₁ = P₂ + ΔP_l = P₂ +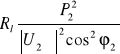 
, (10.26)
Q₁ = Q₂+ΔQ_l = Q₂+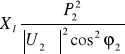 
, (10.27)
|S₁| = |E₁| | I | =
. (10.28)

Natomiast wzdłuż linii występuje spadek napięcia, który powoduje, że w celu uzyskania danego napięcia znamionowego odbiornika |U₂| należy zwiększyć napięcie na początku linii do wartości

E₁ = U₁ = U₂ + (R_l + jX_l) I . (10.29)

Rozkładając napięcie U₂ na składową czynną (równoległą do prądu I) i składową bierną (prostopadłą do prądu I), jak to ilustruje rys.10.4

, (10.30)

możemy obliczyć wartość napięcia U₁ = E₁

U₁ = (|U₂| cosϕ₂ + R_l |I| + j(|U₂| sinϕ₂ + X_l |I|). (`10.31)

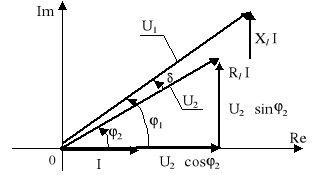
Rys.10.4. Wykres wektorowy realizujący zależność (10.31)

. (10.32)

|ΔU| = |U₁| - |U₂| (10.33) δ |U|_% =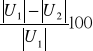 
%. (10.34)

. (10.35)

Kompensacji mocy biernej.

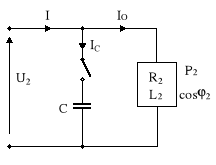
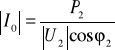
. (10.36)

I = I₀ + I_C = I₀ + j ωC U₂ . (10.37)

Rys.10.5. Układ: źródło-odbiornik-kompensator

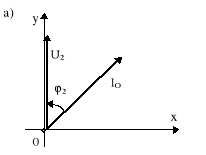
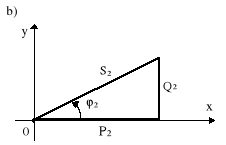
Rys.10.6. Podstawowe wielkości dla układu z rys.10.5: a) wykres wektorowy przy odłączonym kompensatorze; b) trójkąt mocy

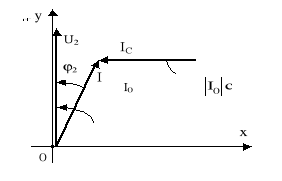
Rys.10.7. Wykres wektorowy dla układu z rys.10.5 przy włączonym kompensatorze (kondensatorze)

|I₀| cosϕ₂ = |I| cosϕ₂′, (10.38) a stąd P₂ = |U₂| |I_O| cosϕ₂ = |U₂| |I| cosϕ₂ . (10.39)

Zagadnienie poprawy współczynnika mocy możemy rozważać w dwojaki sposób:

1. Dobrać tak pojemność C, aby kąt ϕ₂′= 0, tzn. aby prąd źródła I był w fazie z napięciem U₂ i wówczas mówimy o kompensacji całkowitej (rys.10.8). Dla tak postawionego zagadnienia, po kompensacji zachodzi |S₂′| = P₂ ( rys.10.8b). Z rys.10.8b wynika, że

Q₂ = Q_C = P₂ tgϕ₂ = ωC₀ |U₂|², (10.40)

a stąd

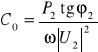
. (10.40a)

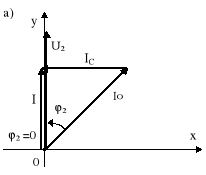
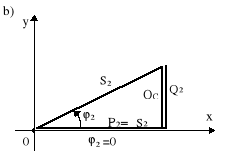
Rys.10.8. Całkowita kompensacja mocy biernej: a) wykres wektorowy; b) trójkąt mocy

2. Dobrać tak pojemność C, aby otrzymać żądany współczynnik mocy cosϕ₂′ > cosϕ₂ (ϕ₂′ < ϕ₂), mówimy wówczas o częściowej kompensacji.

| I | = |I₀ + I_C| =
, (10.41) |I_C| = ωC |U₂| . (10.41a)

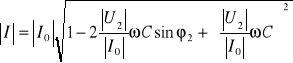
. (10.42)

Q₂ - Q_C = Q = P₂ tgϕ₂′, (10.43)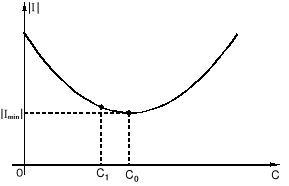

Q₂ = P₂ tgϕ₂, (10.43a)

Q_C = ωC |U₂|², (10.43b)

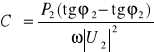
.(10.44)

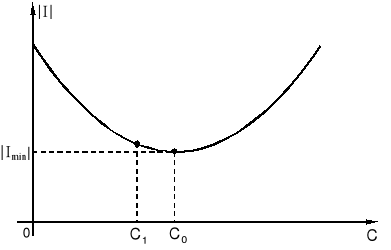
Rys.10.9. Zależność prądu źródła od pojemności kompensującej

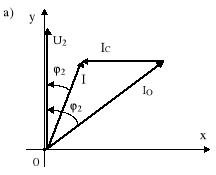
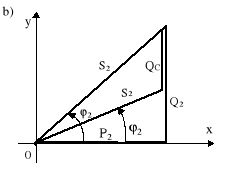
Rys.10.10. Częściowa kompensacja mocy biernej: a) wykres wektorowy; b) trójkąty mocy przed i po kompensacji

10.3. Warunki dopasowania odbiornika do źródła napięcia sinusoidalnego

Maksymalna moc wydawana przez źródło napięcia stałego do odbiornika określona była zależnością

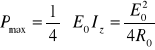
. (10.45)

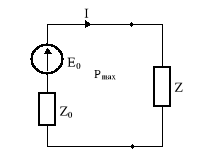
Moc czynna pobierana przez odbiornik o impedancji Z wynosi

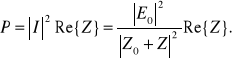
(10.46)
Jeżeli Z₀ = R₀ + jX₀ , Z = R + jX, to ta moc

Rys.10.11. Analizowany obwód

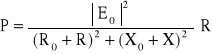
. (10.47)

Zakłada się, że R₀ > 0 i R > 0. Z zależności (10.47) wynika, że moc czynna P jest funkcją dwóch zmiennych R i X.

Warunkiem koniecznym istnienia ekstremum jest, aby
i
.

Pochodne cząstkowe określone są zależnościami (10.48) i (10.48a):

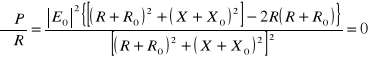
, (10.48)

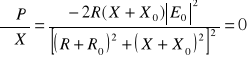
. (10.48a)

Warunki konieczne (10.48) i (10.48a) sprowadzają się do rozwiązania układu równań

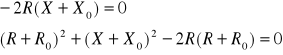
. (10.49)
Rozwiązaniem układu równań (10.49) są wartości

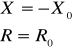
. (10.50)

Punkt (R₀, X₀) spełniający warunek konieczny jest tzw. punktem stacjonarnym. Warunkiem wystarczającym istnienia ekstremum jest, aby określony w następujący sposób wyznacznik W był większy od zera, dla punktu stacjonarnego (R₀, X₀), czyli

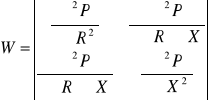
> 0 (10.51)   ponadto gdy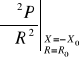
 < 0, (10.52)

to moc czynna P (R,X) przyjmuje wartość maksymalną.

Wyznaczając odpowiednie pochodne w wyznaczniku W mamy:

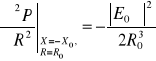
 < 0, (10.53)

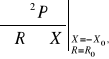
 = 0, (10.53a)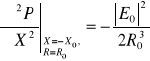
 < 0, (10.53b)

a stąd

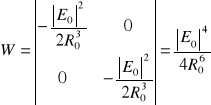
 > 0. (10.53c)

Ponadto

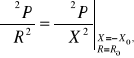
 < 0, (10.53d)
więc dla punktu stacjonarnego (R₀, X₀) istnieje maksimum mocy czynnej P.

Ostatecznie więc:

Warunkiem maksymalnego przekazywania mocy czynnej do odbiornika jest, aby pomiędzy impedancją źródła a impedancją odbiornika zachodziła zależność

Z₀ = Z^* . (10.54)

Warunek (10.54) nosi nazwę warunku energetycznego dopasowania odbiornika do źródła napięcia sinusoidalnego (rys.10.11). Maksymalna moc czynna przekazywana ze źródła do odbiornika oblicza się ze wzoru (10.47) przy warunku (10.54), otrzymując

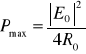
. (10.55)

Moc czynna maksymalna wyraża się takim samym wzorem jak dla źródła napięcia stałego.

1

8

---