W Y K Ł A D 14

FILTRY ELEKTRYCZNE

1. Definicje i klasyfikacja

Rys.14.1. Włączenie filtru elektrycznego między źródło i odbiornik

Pasmo częstotliwości, w którym filtr przepuszcza sygnał bez tłumienia (przy współczynniku tłumienia a równym lub bliskim zeru), jest to pasmo przepustowe - PP. Pasmo częstotliwości, w którym sygnał jest silnie tłumiony ( w filtrze idealnym
, w filtrze rzeczywistym
), jest to pasmo tłumieniowe - PT lub pasmo zaporowe - PZ. Częstotliwość (częstotliwości), która oddziela te pasma nosi nazwę częstotliwości granicznej filtru. Filtr może mieć kilka częstotliwości granicznych.

Rys.14.2. Pasma przepustowe i zaporowe filtrów: a) dolnoprzepustowego, b) górnoprzepustowego,

c) pasmowego, d) zaporowego

W zależności od położenia pasma przepustowego rozróżnia się:

• filtr dolnoprzepustowy, który przepuszcza sygnały o pulsacjach w zakresie od 0 do
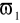
  , a tłumi sygnały o pulsacjach w zakresie od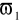
  do ∞,

• filtr górnoprzepustowy, który tłumi sygnały o pulsacjach w zakresie od 0 do
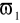
  , a przepuszcza sygnały o pulsacjach w zakresie od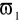
  do ∞,

• filtr pasmowy, który przepuszcza sygnały w zakresie od
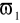
  do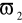
  , a tłumi sygnały o pulsacjach w zakresie od 0 do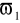
  oraz od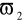
  do ∞,

• filtr zaporowy, który przepuszcza sygnały o pulsacji w zakresie od 0 do
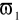
  oraz od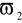
  do ∞, a tłumi sygnały w zakresie od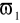
  do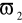
  .

1. Filtry reaktancyjne typu k

Filtr typu k jest czwórnikiem symetrycznym, reaktancyjnym, który musi pracować w warunkach dopasowania falowego, tzn.

, (14.1)

. (14.2)

W stanie dopasowania falowego
(14.3)

(14.3a)

w neperach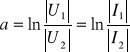
(14.3b) lub w decybelach (1Np=8,685890 dB)

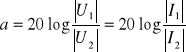
. (14.3c)

(14.4)

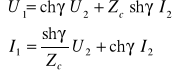
. (14.4a)

W paśmie przepustowym
(14.5)

i wtedy

oraz
. (14.5a)

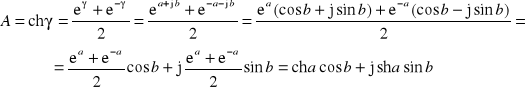
(14.6)

Rys.14.3. Schematy zastępcze czwórników: a) typu T , b) typu Π

Dla czwórnika symetrycznego typu T mamy

oraz
(14.7)

. (14.7a)

Dla czwórnika symetrycznego typu Π mamy

oraz
(14.8)

. (14.8a)

Jeśli elementami powyższych czwórników symetrycznych typu T oraz typu Π będą reaktancje, to stąd wynika, że parametr łańcuchowy A filtru typu k jest zależny od pulsacji ω i jest liczbą rzeczywistą czyli musi spełniać warunki zarówno dla pasma przepustowego, jak i dla pasma tłumieniowego:

, (14.9)

. (14.10)

Pasmo przepustowe

W paśmie tym
i równanie (14.10) jest spełnione, zaś równanie (14.9) przyjmuje postać

, (14.11)

a stąd wynika, że

, (14.11a)

czyli

. (14.11b)

lub

. (14.11c)

Dla czwórnika symetrycznego
, (14.12)

zatem w paśmie przepustowym
. (14.13)

Jednakże parametry łańcuchowe B i C filtrów reaktancyjnych są liczbami urojonymi, a więc warunek (14.13) jest spełniony wówczas, gdy parametry te maja jednakowe znaki. Wtedy impedancja charakterystyczna (14.2) jest liczbą rzeczywistą.

Pasmo tłumieniowe

W paśmie tym
, wobec tego spełnienie równania (14.10) pociąga za sobą warunek

, (14.14)

, (14.14a)

Ponieważ dla
mamy, że
oraz
, więc z równania (14.9) otrzymujemy

, (14.14b)

czyli

. (14.14c)

lub

. (14.11c)

W tym paśmie

(14.15)

i warunek ten jest spełniony jeśli parametry łańcuchowe B i C filtrów reaktancyjnych mają różne znaki. Wobec tego w paśmie tłumieniowym impedancja charakterystyczna może być albo indukcyjna albo pojemnościowa.

Współczynnik fazowy nie może być wyznaczony w paśmie przepuszczania z warunku
gdyż dla
kąt b należy do I lub IV ćwiartki, a dla
- kąt b należy do II lub III ćwiartki płaszczyzny. Jeśli jednak wykorzystamy wzór
lub też
i uwzględnimy, że w paśmie przepustowym impedancja charakterystyczna jest liczbą rzeczywistą oraz przy
mamy

(14.16) to otrzymujemy
. (14.16a)

Wtedy też

(14.17) albo
(14.17a)

2. Filtr dolnoprzepustowy

Rys.14.4. Filtr dolnoprzepustowy: a) schemat typu T ; b) schemat typu Π

Dla czwórnika typu T parametr łańcuchowy

, (14.18)

a dla czwórnika typu Π

. (14.19)

Z porównania powyższych wzorów wynika, że

. (14.20)

W paśmie przepustowym

, (14.21)

czyli

. (14.21a)

Stąd otrzymujemy nierówność

. (14.21b)

Zatem w paśmie przepustowym częstotliwość zawarta jest

, (14.22)

gdzie pulsacja (częstotliwość kątowa) graniczna

. (14.21b)

Dla obu typów filtrów mamy

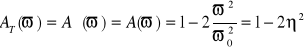
, (14.22)

. (14.22a)

W paśmie przepustowym

, (14.23)

lub

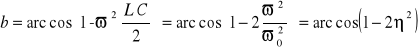
. (14.23a)

Przy
współczynnik fazowy
, przy
mamy
, co oznacza, że współczynnik fazowy w paśmie przepustowym zmienia się od 0 do π , a w paśmie tłumieniowym ma stale wartość równa π - rys.14.5.

Współczynnik tłumienia w paśmie przepustowym filtru jest równy zeru, a w paśmie tłumieniowym ze wzoru (14.6) mamy

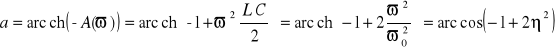
, (14.24)

czyli w miarę wzrostu częstotliwości współczynnik tłumienia rośnie (do nieskończoności) - rys.14.5.

Rys.14.5. Charakterystyki zmienności współczynników a i b filtru dolnoprzepustowego w funkcji częstotliwości

Impedancja falowa w przypadku schematu T

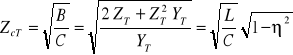
. (14.25)

Z powyższego wzoru wynika, że

• przy
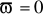
  pulsacja względna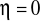
  i wtedy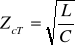
  ,

• przy
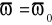
  pulsacja względna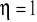
  i wtedy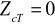
  ,

• przy
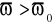
  pulsacja względna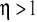
  i wtedy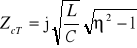
  , co oznacza, że w paśmie tłumieniowym impedancja charakterystyczna filtru dolnoprzepustowego o schemacie T ma charakter indukcyjny.

Rys.14.6. Charakterystyki zmienności w funkcji częstotliwości impedancji charakterystycznych filtru dolnoprzepustowego: a) o schemacie typu T ; b) o schemacie typu Π

W przypadku filtru o schemacie typu Π impedancja charakterystyczna

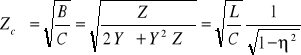
. (14.26)

Z powyższego wzoru wynika, że

• przy
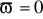
  pulsacja względna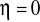
  i wtedy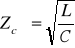
  ,

• przy
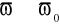
  pulsacja względna
  i wtedy
  ,

• przy
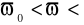
  pulsacja względna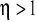
  i wtedy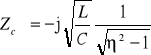
  , co oznacza, że w paśmie tłumieniowym impedancja charakterystyczna filtru dolnoprzepustowego o schemacie Π ma charakter pojemnościowy,

• przy
  pulsacja względna
  i wtedy
  .

1. Filtr górnoprzepustowy

Rys.14.7. Filtr górnoprzepustowy: a) o schemacie typu T ; b) o schemacie typu Π

, (14.27)

. (14.28)

. (14.29)

W paśmie przepustowym

, (14.30)

czyli

. (14.31a)

Stąd otrzymujemy nierówność

. (14.31b)

Zatem w paśmie przepustowym częstotliwość zawarta jest

, (14.31c)

gdzie pulsacja (częstotliwość kątowa) graniczna
. (14.31d)

Dla obu typów filtrów mamy

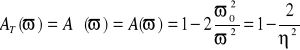
, (14.32)

gdzie pulsacja względna odniesiona do pulsacji granicznej
. (14.32a)

W paśmie przepustowym
, (14.33)

lub

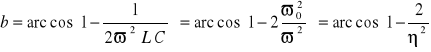
. (14.33a)

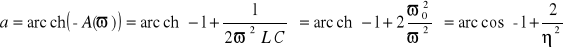
, (14.34)

Rys.14.8. Charakterystyki zmienności współczynników a i b filtru górnoprzepustowego w funkcji częstotliwości

Impedancja falowa w przypadku schematu T

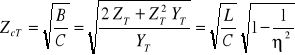
. (14.35)

• przy
  pulsacja względna
  i wtedy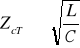
  ,

• przy
  pulsacja względna
  i wtedy
  ,

• przy
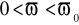
  pulsacja względna
  i wtedy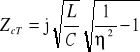
  , co oznacza, że w paśmie tłumieniowym impedancja charakterystyczna filtru górnoprzepustowego o schemacie T ma charakter indukcyjny,

• przy
  pulsacja względna
  i wtedy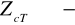
  .

Rys.14.8. Charakterystyki zmienności w funkcji częstotliwości impedancji charakterystycznych filtru górnoprzepustowego: a) o schemacie typu T ; b) o schemacie typu Π

W przypadku filtru o schemacie typu Π impedancja charakterystyczna

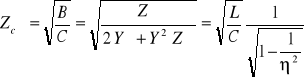
. (14.36)

Z powyższego wzoru wynika, że

• przy
  pulsacja względna
  i wtedy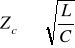
  ,

• przy
  pulsacja względna
  i wtedy
  ,

• przy
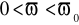
  pulsacja względna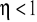
  i wtedy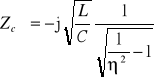
  , co oznacza, że w paśmie tłumieniowym impedancja charakterystyczna filtru górnoprzepustowego o schemacie Π ma charakter pojemnościowy,

• przy
  pulsacja względna
  i wtedy
  .

1. Filtr pasmowy i filtr zaporowy

Filtr pasmowy Rys.14.9. typu Π

Parametr łańcuchowy filtru z powyższego rysunku

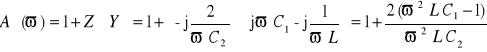
. (14.37)

W paśmie przepustowym
, (14.38)

czyli

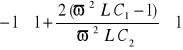
. (14.38a)

Powyższą nierówność rozpatrzymy dla przypadku granicznego

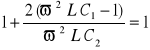
, (14.39)

skąd otrzymujemy

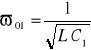
. (14.39a)

W drugim przypadku granicznym

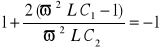
, (14.40)

skąd otrzymujemy

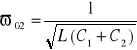
. (14.40a)

W paśmie przepustowym

, (14.41)

lub

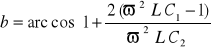
. (14.41a)

Przy
współczynnik fazowy
, przy
współczynnik
, co oznacza, że współczynnik fazowy w paśmie przepustowym zmienia się od -π do 0 - rys.14.10.

Rys.14.10. Charakterystyki zmienności współczynników a i b filtru pasmowego w funkcji częstotliwości

Zadaniem filtru zaporowego jest przenoszenie wszystkich sygnałów częstotliwości z wyjątkiem pewnego określonego pasma od
do
. W gałęziach podłużnych takiego filtru znajdują się obwody rezonansu prądów, a w gałęziach poprzecznych obwody rezonansu napięć - rys.14.11.

Rys.14.11. Filtr zaporowy

14.6. Filtry RC

Rys.14.12. Filtr dolnoprzepustowy RC

Dla filtru typu T z powyższego rysunku mamy

oraz
(14.42)

i wtedy

, (14.43)

. (14.43a)

. (14.44)

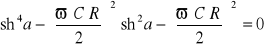
. (14.45)

Rozwiązaniem tego równania jest

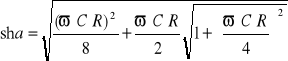
. (14.45a)

Umownie określamy pulsację graniczną ze wzoru
(14.46)

i wtedy wykres współczynnika tłumienia przedstawia rys.14.13.

Rys.14.13. Wykres współczynnika tłumienia dolnoprzepustowego filtru RC

Dla pulsacji granicznej
, tj. dla
ze wzoru (14.45a) mamy, że
czyli
.

Górnoprzepustowego filtru RC

Rys.14.14. Górnoprzepustowy filtr RC

oraz
(14.47)

i wtedy

, (14.48)

. (14.48a)

. (14.49)

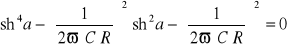
. (14.50)

Rozwiązaniem tego równania jest

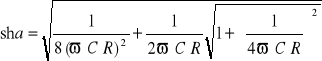
. (14.50a)

Rys.14.15. Wykres współczynnika tłumienia górnoprzepustowego filtru RC

Zakresem przepuszczania jest zakres pulsacji od
do nieskończoności, przy czym pulsację graniczna oblicz się umownie z wyrażenia

(14.50b)

---