Zestaw zadań do samodzielnego rozwiązania
Poniższy zestaw zadań podzielony został na dwie grupy:
typowe - ze wszystkimi założeniami, gdzie wymagana jest tylko znajomość odpowiednich wzorów;
problemowe - bardziej skomplikowane, wymagające często przyjęcia dodatkowych założeń i komentarza.
Zadanie 1
Inwestujesz dziś 1000 zł. Jakiej kwoty, przy stopie 10 %, spodziewasz się za:
1 rok
2 lata
5 lat
Zadanie 2
Kapitał 1000 zł został ulokowany na trzy lata na 8% rocznie. Jaką kwotę otrzymasz po tym okresie oszczędzania, przy dwukrotnej kapitalizacji odsetek w roku?
Zadanie 3
Spodziewasz się, że cena działki rolnej w okolicach Jeleniej Góry będzie wynosic za dwa lata 25 000 zł. Jakiej równej wysokości wkłady wnoszone na koniec kolejnych miesięcy pozwolą zgromadzić Ci w ciągu 2 lat niezbędny fundusz na jej zakup. Bank stosuje miesięczną kapitalizację przy rocznej stopie procentowej wynoszącej 6%
Zadanie 4
Inwestujesz w ciągu 3 lat po 1000 zł na koniec każdego roku. Jaka będzie łączna wartość tych kwot po upływie tego okresu, przy stopie 10 %. Jak zmieni się wartość jeśli wpłaty będą dokonywane na początek każdego okresu.
Zadanie 5
Inwestor A przez trzy miesiące wpłacał na koniec każdego miesiąca na rachunek bankowy następujące sumy: 1000, 1500, 3000 zł. Oprocentowanie rachunku wynosi 12% w skali rocznej przy miesięcznej kapitalizacji. Inwestor B dokonywał wpłat w tej samej wysokości, przy identycznym oprocentowaniu i kapitalizacji, na początek każdego miesiąca. Jaką kwotę zgromadzą inwestorzy za trzy miesiące na swoich rachunkach?
Zadanie 6
Za rok otrzymasz 1000 zł. Taką samą kwotę za 2, 3 i 5 lat. Jaką wartość ma dziś dla Ciebie każda z tych kwot, przy stopie aktualizacji 5%.
Zadanie 7
Oblicz wysokość miesięcznej raty annuitetowej dla kredytu hipotecznego 300 000 zł zaciągniętego na okres 10 lat, przy stopie 7%.
Zadanie 8
Jaka jest bieżąca łączna wartość 3 wpłat po 1000 zł, dokonywanych na koniec każdego roku, a jaka gdy wpłaty będą dokonywane na początek każdego okresu, przy stopie 5%.
Zadanie 9
Począwszy od roku 2015 do 2020 masz otrzymywać 10 000 rocznie. Jaka jest bieżąca wartość tych płatności?
Zadanie 10
Projekt, którego przedmiotem jest nowa fabryka, ma kosztować 47,2 mln zł. Wiadomo, że po 12-letnim okresie eksploatacji należy dokonać gruntownej modernizacji przedsiębiorstwa. Koszt tego przedsięwzięcia będzie równy 70% pierwotnie poniesionych wydatków.
Ile należy odkładać rocznie jeśli wiadomo, że firma jest w stanie lokować wolne środki pieniężne na lokaty oprocentowane 9% w skali roku.
Zadanie 11
Za 15 lat będziesz potrzebował(a) 20 000 €, na początek każdego roku, na studia dla swojego dziecka.
Jaką kwotę musisz dziś ulokować w banku, przy oprocentowaniu 3% w skali roku, aby opłacić całe 5-letnie studia.
Jaka kwotę powinieneś miesięcznie wpłacać na rachunek, przy tym samym oprocentowaniu, dla opłacenia tychże studiów, zamiast jednorazowej dzisiejszej wpłaty.
Zadanie 12
Przepływy pieniężne na zakończenie każdego z kolejnych czterech lat wynoszą: 3000, 3500, 4000, 5000 zł. Ile wyniesie wartość bieżąca tych przepływów, jeżeli:
stopa procentowa wynosi 20%
stopa procentowa w kolejnych latach wynosi odpowiednio: 20, 18, 17, 15%?
Zadanie 13
Jakiej minimalnej kwoty powinieneś zażądać za 0,1ha ziemi, wiedząc że możesz ją wydzierżawić za 1000 zł miesięcznie.
Zadanie 14
Jesteś w stanie odkładać od dzisiaj co miesiąc 200 zł. na poczet przyszłych studiów swojego dziecka. Ile będzie ono otrzymywało miesięcznie podczas swojej nauki na uczelni wyższej, jeżeli oczekiwana stopa procentowa wynosi 5%. (dokonaj własnych założeń niezbędnych do wyliczenia tego zadania)
Zadanie 15
Student podejmujący 6-letnie studia medyczne dostaje od rodziców 100 000 zł, za które po ukończeniu studiów zamierza zakupić mieszkanie.
Rozważa 2 warianty:
Zakłada lokatę oprocentowaną 6% w skali roku;
Znajomy proponuje mu udział w przedsięwzięciu - współwłasność w firmie wykonującej roboty ziemne. Jako wkład ma zapewnić koparkę, której cena wynosi 100 000 zł. Na podstawie przedstawionego biznesplanu dowiedział się, że ma otrzymywać na koniec każdego roku 25% zysków firmy. Ponadto po upływie 6 lat znajomy odkupi od niego udziały w firmie za 50 000 zł.
Planowane zyski firmy w zł.
1 |
2 |
3 |
4 |
5 |
6 |
40 000 |
60 000 |
70 000 |
80 000 |
80 000 |
80 000 |
Skomentuj, która opcja jest dla tego studenta bardziej korzystna i dlaczego?
Zadanie 16
Podejmujesz swoją pierwszą pracę i już myślisz o swojej emeryturze. Chcesz aby w przyszłości jej roczna kwota wynosiła przynajmniej 24 000 PLN i była wypłacana na początek każdego roku. Ile musisz odkładać rocznie do wieku emerytalnego, przy stopie 5%, aby otrzymywać taką emeryturę.
Zadanie 17
Jesteś właścicielem firmy świadczącej usługi galwaniczne, zysk netto twojej firmy wynosi obecnie 120 000 zł rocznie. Chcąc zwiększyć udział w rynku planujesz w ciągu trzech lat zwiększyć swoje moce produkcyjne, a to wiąże się z koniecznością zakupu nowej linii produkcyjnej. Wiesz jednak, że zakumulowany przez ten okres kapitał (zysk firmy) nie wystarczy na dokonanie inwestycji. Postanawiasz, że dodatkowo zaciągniesz kredyt na 3 lata spłacany w 3 ratach, równych Twoim rocznym wolnym środkom pieniężnym (raty obejmują spłatę kapitału oraz odsetki). Wielkość tych środków prognozujesz na poziomie 200 000zł rocznie (po zwiększeniu mocy produkcyjnych). Ile będziesz w stanie maksymalnie zapłacić za linię produkcyjną jeżeli:
stopa oprocentowania lokat - 5 %
oprocentowanie kredytu - 9 %
Zadanie 18
Posiadasz ziemię, za którą w obecnym stanie otrzymałbyś za dzierżawę 20 000 rocznie. Postanawiasz jednak przed jej wydzierżawieniem trwale polepszyć zdolności produkcyjne gleby. W wyniku melioracji roczna kwota dzierżawy może wzrosnąć do 25 000 zł. Koszt tego zabiegu wynosi 50 000 zł. W jakich warunkach projekt ten będzie opłacalny.
Zadanie 19
Wraz z grupą podróżników planujesz wybrać się, po sześciu latach przygotowań (licząc od teraz), na 3-letnią wyprawę dookoła świata. Roczny koszt takiej ekspedycji to 100 000 zł. Aby sfinansować całą podróż postanawiasz wraz ze współtowarzyszami odkładać do momentu wyjazdu, po 16 000 zł rocznie. Ponadto Wasz sponsor zobowiązał się, że w dniu rozpoczęcia wyprawy przeznacza jednorazowo na ten cel 120 000 zł. Stopa procentowa 8% w skali roku
Czy uzbierana kwota, wystarczy na sfinansowanie całej wyprawy?
Jeśli nie, to jaką kwotę musielibyście wpłacać rocznie na konto, aby Wasza podróż doszła do skutku?
Zadanie 20
Przedsiębiorstwo transportowe kupuje dzisiaj samochód ciężarowy za 150.000zł. Przewiduje się, że jego eksploatacja w ciągu najbliższych 5 lat będzie przynosiła rocznie 30.000 zł czystego dochodu. Po upływie tego czasu można będzie jeszcze sprzedać ten samochód za 40.000 zł. Proszę policzyć czy inwestycja ta będzie opłacalna jeżeli aktualne oprocentowanie kredytów wynosi 10%.
Zadanie 21
Gmina zamierza sprzedać na przetargu działający jeszcze, ale przynoszący straty zakład butelkujący wodę mineralną. Ocenia się, że po dodatkowych inwestycjach w wysokości 400 000 zł. i uporządkowaniu działalności, zakład ten może przynosić zyski w wysokości 250 000 zł. rocznie przez najbliższe 8 lat. Jaką maksymalnie cenę można za ten zakład zaoferować, jeżeli przedsiębiorca oczekuje minimalnej stopy zwrotu od zainwestowanego kapitału w wysokości 10%?
Zadanie 22
Masz możliwość uzyskania specjalnego kredytu na zakup zabytkowego budynku i późniejszy jego remont. Koszty zakupu i koniecznego remontu doprowadzą budynek do stanu, w którym jego oczekiwana cena rynkowa przekroczy o 20% wszystkie poniesione koszty. Dzisiejsze koszty zakupu i remontu budynku to 900 000 zł - w całości są pokryte kredytem.
Warunki kredytu - 5 lat karencji, w czasie której kredytobiorca nie płaci nawet odsetek. Po tym okresie spłata w pięciu równych rocznych kwotach (rata z odsetkami) po 420 000 zł. Czy przy dzisiejszym oprocentowaniu kredytu (12%) zdecydujesz się na tę transakcję i dlaczego?
Zadanie 23
Rozważasz możliwość kupna 10 ha ziemi po 5 000zł za hektar. Spodziewasz się, że ziemia ta będzie nabierać wartości i za 5 lat będzie warta 10 000 zł/hektar. Posiadasz obecnie tylko 20 000 Złotych. By kupić tę ziemię musisz wziąć kredyt, którego koszt obecnie wynosi 12% w skali rocznej.
Uzasadnij swoją decyzję odpowiednim rachunkiem biorąc pod uwagę również elementy ryzyka związane z tą transakcją.
Zadanie 24
Firma deweloperska rozważa zakup działki ziemi, którą przewiduje pod zabudowę za 5 lat. Ocenia się, że działka ta będzie wówczas miała wartość rynkową 12 mln zł. Obecnie wolne środki firmy mogą być zainwestowane w inne przedsięwzięcie o podobnym stopniu ryzyka obiecujące dochód w wysokości 15% w skali rocznej. Jaka jest maksymalna kwota, którą firma może zaoferować na ogłoszonym przetargu?
Zadanie 25
Rząd małego kraju wyspiarskiego rozważa budowę nowego terminalu paliw płynnych. Jego budowa ma przynieść zmniejszenie kosztu dostaw paliw do kraju przy niezmienionej cenie na rynku. Terminal stanowi uzupełnienie już istniejącego systemu zbiorników. Po zakończeniu inwestycji cały system zostanie oddany prywatnej firmie eksploatującej w drodze przetargu. Oczekuje się, że nowy czynsz będzie wyższy od płaconego poprzednio.
Techniczny okres eksploatacji systemu to 10 lat. Po tym czasie konieczne będą nowe inwestycje odtwarzające.
Przedmiotem przetargu jest prawo eksploatacji systemu przez 10 lat.
Proszę ocenić o ile powinna wzrosnąć cena wywoławcza przetargu (w stosunku do płaconego wcześniej czynszu), jeżeli koszt inwestycji oceniany na 5mln $ jest w całości finansowany kredytem spłacanym w pięciu równych rocznych ratach (wraz z odsetkami), a koszt kredytu wynosi 8% w skali rocznej. Inwestycja trwa 1 rok, spłaty rozpoczynają się w pierwszym roku eksploatacji.
Oczekiwana przez rząd stopa zwrotu inwestycji to 12%.
Zadanie 26
Wrocław zamierza organizować duże międzynarodowe zawody sportowe. Potrzebny do tego jest stadion spełniający wszelkie standardy międzynarodowe. Koszt jego budowy, szacowany na $ 50 mln znacznie przekracza możliwości budżetu miasta. Firma angielska proponuje budowę obiektu, pod warunkiem uzyskania prawa do eksploatacji tego stadionu przez 8 lat. Po tym okresie stadion ma być przekazany miastu nieodpłatnie.
Firma szacuje, że po roku budowy, w pierwszym roku eksploatacji wpływy od użytkowników wyniosą $ 12,5 mln. Przez kolejne 2 lata wpływy będą wzrastać o 30% rocznie, po czym ustabilizują się na poziomie z roku trzeciego. Koszty eksploatacji szacowane są na 50% wpływów, zaś koszt kapitału dla tej inwestycji wynosi 10% w skali roku.
Co można powiedzieć o opłacalności tego przedsięwzięcia?
Jak na decyzję konsorcjum może wpłynąć fakt, odpłatnego przekazania stadionu miastu w roku dziewiątym za kwotę $ 13 mln?
Zadanie 27
Koszt planowanej budowy Aquaparku szacowany jest na 120 mln zł. Miasto liczy na dofinansowanie UE w wysokości 80 mln zł. Pozostała kwota pochodzić będzie z zaciągniętego kredytu.
Trzy instytucje złożyły oferty kredytu na brakujące 40 mln zł
Spłata w 10 równych rocznych ratach po 4 mln zł przy 10% oprocentowaniu
4 lat karencji (bez płatności odsetek), po której spłata w pięciu ratach rocznych po 10mln każda
10 lat karencji (bez płatności odsetek), po których spłata w 10 równych ratach po 10 mln każda
Którą z ofert powinno miasto przyjąć przy założeniu 10% stopy dyskontowej?
Zadanie 28
Poniższa tabela przedstawia przepływy netto dla projektów A i B. Na podstawie poznanej formuły szacowania IRR ustal wewnętrzną stopę zwrotu dla każdego z projektów. Sprawdź wyniki wykorzystując gotową formułę w arkuszu kalkulacyjnym (np. Excel). Który z projektów zaakceptujesz, w sytuacji gdy wykluczają się one wzajemnie.
Rok |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
A |
-60 |
20 |
20 |
20 |
20 |
20 |
20 |
B |
-72 |
45 |
22 |
20 |
12 |
12 |
12 |
Zadanie 29
Ustal zmodyfikowaną wewnętrzną stopę zwrotu (MIRR) dla inwestycji o planowanym okresie eksploatacji wynoszącym 6 lat, dla której wartość nakładów początkowych wynosi 1mln zł
w pierwszych 2 latach projekt wygeneruje ujemne przepływy pieniężne netto o wartości 0,95 mln zł oraz 1 mln zł,
w kolejnych latach inwestycja będzie przynosić dodatnie przepływy pieniężne na poziomie 1,2 mln zł w każdym z tych okresów.
Oczekiwana stopa zwrotu z tego przedsięwzięcia ustalona została na 10% rocznie, natomiast stopa reinwestycji równa jest 6%.
Zadanie 30
Jesteś osobą odpowiedzialną za ocenę projektów w jednym z Urzędów Gminy. Masz do przeanalizowania 4 projekty A, B, C, D. Przepływy netto projektów prezentuje poniższa tabela. Roczny koszt kapitał wynosi 5%.
Które projekty zaakceptujesz do dalszej analizy i dlaczego?
Które z nich ostatecznie przyjmiesz do realizacji i jakie będą tego korzyści, jeśli budżet zarezerwowany na powyższe cele wynosi 400 000 zł i istnieje możliwość częściowej realizacji projektów.
Okres |
0 |
1 |
2 |
3 |
Projekt A |
-150 000 |
45 000 |
45 000 |
100 000 |
Projekt B |
-100 000 |
30 000 |
30 000 |
70 000 |
Projekt C |
-200 000 |
50 000 |
50 000 |
120 000 |
Projekt D |
-250 000 |
70 000 |
70 000 |
150 000 |
Załącznik 1. Dyskontowanie i naliczanie wartości przyszłej - formuły
Formuła 1
Wartość przyszła pieniądza
![]()
Formuła 2
Wartość przyszła pieniądza przy m kapitalizacjach w ciągu roku
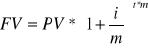
Formuła 3
Wartość bieżąca pieniądza
![]()
Formuła 4
Wartość bieżąca pieniądza przy m kapitalizacjach w ciągu roku
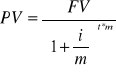
Formuła 5
Przyszła wartość rat annuitetowych
![]()
- płatności z dołu (na koniec okresu)
![]()
- płatności z góry (na początek okresu)
Formuła 6
Bieżąca wartość rat annuitetowych
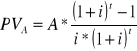
- płatności z dołu (na koniec okresu)
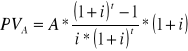
- płatności z góry (na początek okresu)
Formuła 7
Wielkość raty annuitetowej przy znanej przyszłej wartości (kapitału)
![]()
Formuła 8
Wielkość raty annuitetowej przy znanej bieżącej wartości (kapitału)
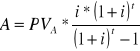
Formuła 9
Wartość przyszła zmiennych płatności
![]()
Jeśli płatności występują na początek okresu (z góry), to dolna granica sumowania t=0, a jeżeli na koniec okresu (z dołu), to dolna granica sumowania t=1 (dotyczy również wzoru na wartość bieżącą zmiennych płatności)
Formuła 10
Wartość bieżąca zmiennych płatności
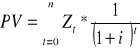
Formuła 11
Wartość bieżąca zmiennych płatności i stóp procentowych
![]()
Formuła 12
Renta gruntowa
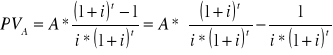
![]()
- (płatne na koniec okresu)
![]()
- (płatne na początek okresu)
Wartość zaktualizowana netto (wartością dzisiejszą netto) - NPV (z angielskiego Net Present Value)
![]()
gdzie:
NCF - netto cash flow
Wewnętrzna stopa zwrotu - IRR (Internal Rate of Return)
IRR = i dla którego
NPV=![]()
Zmodyfikowana IRR - MIRR
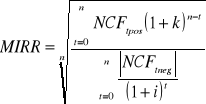
gdzie:
NCFt neg - ujemny przepływ netto projektu z okresu t,
NCFt pos - dodatni przepływ netto projektu z okresu t
i - stopa dyskontowa
k - stopa reinwestycji
n - liczba okresów „życia” projektu
Wskaźnik NPV
NPVR = ![]()
, gdzie
NPVR - wskaźnik NPV
PVI - wartość bieżąca nakładów inwestycyjnych
0
![]()
Wyszukiwarka
Podobne podstrony:
ZESTAW F ANALIZA EKONOMICZNA
AE, Analiza Ekonomiczna
Zestaw zadan - analiza nakladow i wynikow (z komputerami), studia, pomoce naukowe - repetytoria, eko
Wskazniki z AE, Archiwum, Semestr VII, Analiza ekonomiczna
zestaw D,F na koło, ANALIZA EKONOMICZNA - zestaw D, ANALIZA EKONOMICZNA - kolokwium
AE egzamin, Archiwum, Semestr VII, Analiza ekonomiczna
Analiza ekonomiczna Zestaw 1
W11 analiza ekonomiczna
Analiza ekonomiczna ocena efektywności inwestycji
ANALIZA EKONOMICZNA teoria3
Rachunkowość Warunki pozyskiwania kredytu, Technik administacji, Rachunkowość i analiza ekonomiczna
test 8, studia, Analiza ekonomiczno finansowa
analiza ekonomiczna przedsiębiorstwa - cz. 5, analiza finansowa
Analiza ekonomiczna notatki na koło
Metody analizy?ektywności ekonomicznej P1
Analiza ekonomiczna sciaga
Analiza ekonomiczna teoria (26 strony) id 60090 (2)
więcej podobnych podstron