PYTANIE 8
8.1 Geometria kryształów.
Rodzaje ciał stałych: kryształy, ciała amorficzne, ciała niekrystaliczne, szkła, ciecze.
Ciała amorficzne - możliwe uporządkowanie krótko zasięgowe np. polimery, żele, szkła. Kryształy - uporządkowanie w całej objętości. Badania dyfrakcji promieniowana rentgenowskiego wykazały, że kryształy są utworzone z periodycznej sieci atomów. Ich konstrukcje stanowi powtarzający się wzór.
Idealny kryształ - zbudowany z powtarzających się w przestrzeni identycznych jednostek strukturalnych. Taką jednostką strukturalną mogą być atomy (np. metale: miedz, złoto, srebro, żelazo, litowce) ale też mogą to być struktury zawierające wiele atomów, czy cząsteczek (molekuł, np. białka - niezwykle złożone strukturalnie). Idealna struktura krystaliczna to wynik minimalizacji energii, dokładniej energii swobodnej.
Równanie opisujące strukturę kryształu:
Struktura kryształu = siec + baza
gdzie:
a) sieć - przestrzenny układ punktów, zwanych węzłami (matematyczna
abstrakcja),
b) baza - grupa atomów znajdująca się w węźle sieci.
Kryształ rzeczywisty zawiera defekty - niedoskonałości sieci krystalicznej. Wpływ wywierany przez defekty w krysztale może być nader pożądany lub nader niekorzystny.
8.2 Pojecie sieci krystalicznej.
Sieć krystaliczna - powtarzający się w nieskończoność ten sam wzór. Sieć się nie zmienia pod wpływem translacji. Zdefiniowana jest przez trzy wektory translacji sieci oznaczone jako: a1, a2, a3.
Sieć oglądana z punktów r i r' musi być taka sama, zatem spełniony jest wzór:
gdzie: u1, u2, u3 dowolne liczby całkowite.
Wektory a1, a2, a3 tworzą krawędzie równoległościanu, elementu składowego struktury krystalicznej o najmniejszej objętości, nazywanego komórką elementarną kryształu. Wektory a1, a2, a3 wyznaczają układ osi krystalicznych.
Komórka - elementarny podstawowy składnik budowy kryształu: „cegła”, którą zabudowuje się przestrzeń kryształu.
Komórka elementarna charakteryzuje się najmniejszą objętością. Objętość równoległościanu o bokach a1, a2, a3 jest równa:
Istnieje inny sposób wyboru komórki elementarnej. Wówczas określa się ja mianem komórki Wignera - Seitza.
8.3 Prosta i płaszczyzna sieciowa.
![]()
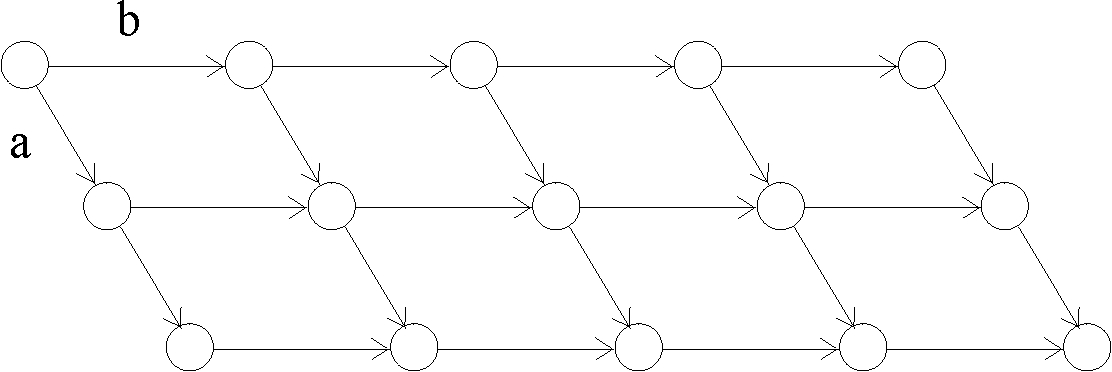
8.4 Parametry sieciowe w układzie trójwymiarowym.
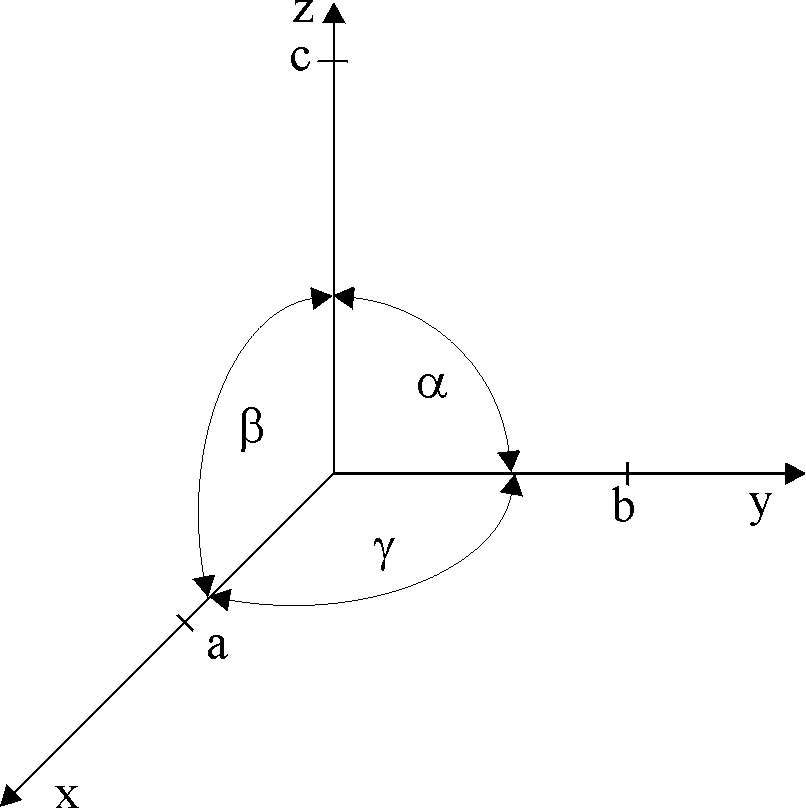
kąty:
α (kąt między osiami Y i Z),
β (kąt między osiami X i Z),
γ (kąt między osiami X i Y),
periody identyczności :
a (period identyczności wzdłuż osi X),
b (period identyczności wzdłuż osi Y),
c (period identyczności wzdłuż osi Z).
Wyszukiwarka
Podobne podstrony:
PYTANIE 9, Mechanika i budowa maszyn, Semestr VII, Fizyka
PYTANIE 3, Mechanika i budowa maszyn, Semestr VII, Fizyka
PYTANIE 5, Mechanika i budowa maszyn, Semestr VII, Fizyka
PYTANIE 10, Mechanika i budowa maszyn, Semestr VII, Fizyka
PYTANIE 11, Mechanika i budowa maszyn, Semestr VII, Fizyka
patenty1, Mechanika i budowa maszyn, Semestr VII, Ochrona patentowa
3, Mechanika i budowa maszyn, Semestr VII, Ochrona patentowa
pytania 2012-2013, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mechanika i Budowa
przykladowe pytania, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Technologie materiałów inż
ściąga z Fizy semI, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mechanika i Budowa
Płyny opracowane pytania, Mechanika i Budowa Maszyn PWR MiBM, Semestr III, Mechanika Płynów, Mechani
zaliczenie odpowiedzi, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mechanika i Bud
Inspiracja utworem... - referat, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mecha
Siemens, Mechanika i budowa maszyn, Semestr VI, Informatyka w eksploatacji pojazdów, Prezentacja
polimery, Politechnika Lubelska (Mechanika i Budowa Maszyn), Semestr 1, Tworzywa polimerowe
zadania z egzaminu, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mechanika i Budowa
SYSTEM TOLL, Mechanika i budowa maszyn, Semestr VI, Informatyka w eksploatacji pojazdów, Prezentacja
GRUNDIG, Mechanika i budowa maszyn, Semestr VI, Informatyka w eksploatacji pojazdów, Prezentacja
termoogniwo, Dokumenty PWZS Zamość, Mechanika i Budowa maszyn I semestr
więcej podobnych podstron