Θ - nadwyższka temperatury pręta w stosunku do temperatury otoczenia;
Wartość nadwyższki temperatury na końcu pręta wyraża się wzorem:
![]()
Strumień ciepła doprowadzony do pręta wyraża się wzorem:
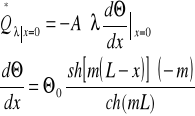
![]()
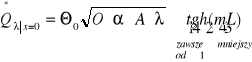
ŻEBRA
h A
δ
b
h - wysokość żebra
b - długość żebra
δ - grubość żebra
A - przekrój żebra
Żebra proste traktujemy jako pręty na końcu izolowane.
![]()
Przeważnie b >> δ dlatego można pominąć (δ = 0) w stosunku do długości `b'.
![]()
δ/2
![]()
POWIERZCHNIE OŻEBROWANE
h
t1, α1 A1Ż A1
γ1
δ
b
A1OŻ
γ2 s
s
λs
γm
t2, α2
δs
powierzchnia żebra i powierzchnia między żebrowa
powierzchnia nałożenia żebra
powierzchnia żebra
s - podziałka żeber (odległość między żebrami)
δs - grubość ścianki
γm - średnia temperatura żebra
n - ilość żeber
Dla jednego żebra:
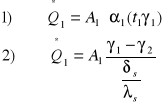
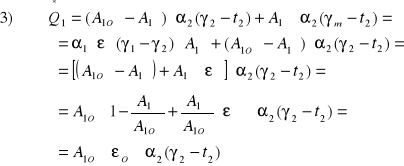
gdzie:
![]()
- sprawność żebra
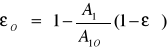
- sprawność powierzchni żebra
Z powyższych równań wynikają zależności:
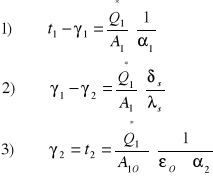
Stopień ożebrowania powierzchni:
![]()
Po zsumowaniu stronami otrzymamy wyrażenie:
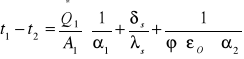
Po przekształceniu wyrażenia otrzymamy wzór na strumień ciepła przekazywany przez ściankę ożebrowaną:
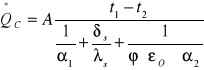
Sprawność żebra prostego:
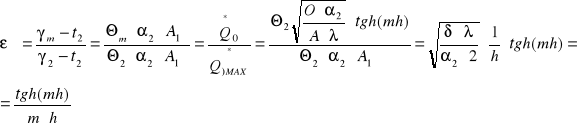
εŻ
1 wykres sprawności żebra prostego
mh
Żebra o innych kształtach - sprawność dobiera się z gotowych wykresów.
Żebra stosujemy, gdy są duże różnice współczynników α1 i α2 w celu zwiększenia wymiany ciepła.
α1, ϕ1, εŻ1 α2, ϕ2, εŻ2
Ogólny wzór ma postać:
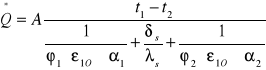
WYBRANE ZAGADNIENIA PRZEWODZENIA CIEPŁA
PRZEWODENIE CIEPŁA Z WEWNĘTRZNYMI ŹRÓDŁAMI CIEPŁA
Dla ścianki płaskiej
γ
qv = idem
γ1 λ = idem
qλx qλx+dx dQv
γ2
x
dx
δ
Źródła ciepła:
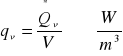
- gęstość źródeł ciepła
![]()
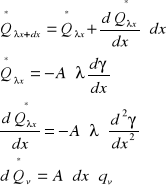
Podstawiając otrzymamy:
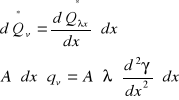
![]()
- równanie różniczkowe opisujące rozkład temperatury w płycie, gdzie wydzielane ciepło jest stałe qv = idem; λ = idem;
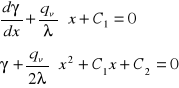
Stałe wyznaczmy z warunków brzegowych:
x = 0; γ = γ1
x = δ; γ = γ2
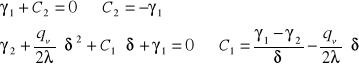
Podstawiając stałe do równania otrzymamy równanie rozkładu temperatur w płycie płaskiej:
![]()
Wyszukiwarka
Podobne podstrony:
lamperski, W9 - mechaniczno-energetyczny
lamperski, W9 - mechaniczno-energetyczny
lamperski, W9 - mechaniczno-energetyczny
lamperski, W9 - mechaniczno-energetyczny
lamperski, W9 - mechaniczno-energetyczny
lamperski, W9 - mechaniczno-energetyczny
lamperski, W9 - mechaniczno-energetyczny
lamperski, W9 - mechaniczno-energetyczny
lamperski, W9 - mechaniczno-energetyczny
lamperski, W9 - mechaniczno-energetyczny
lamperski, W9 - mechaniczno-energetyczny
lamperski, W9 - mechaniczno-energetyczny
mościcka, W9 - mechaniczno-energetyczny
chruścielski, W9 - mechaniczno-energetyczny
szulc, W9 - mechaniczno-energetyczny
pawlak-kruczek, W9 - mechaniczno-energetyczny
4669, W9 - mechaniczno-energetyczny
gnutek, W9 - mechaniczno-energetyczny
hardy, W9 - mechaniczno-energetyczny
więcej podobnych podstron