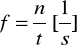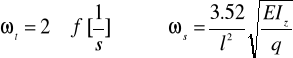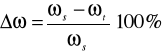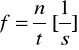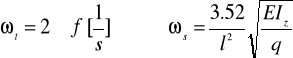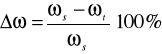Ćwiczenie nr V
DRGANIA POPRZECZNE (GIĘTNE) PRĘTÓW
1. Cel ćwiczenia
Celem ćwiczenia jest pomiar częstości podstawowej drgań poprzecznych (giętnych) pręta dla różnych długości i materiałów. Następnie porównano wyniki pomiarów częstości drgań tłumionych; tarciem wewnętrznym i konstrukcyjnym w miejscu zamocowania pręta oraz oporami zewnętrznymi powietrza dla ![]()
z obliczeniami teoretycznymi.
2. Podstawy teoretyczne drgań poprzecznych (giętnych) prętów
Rozważono pręt prosty wykonany dla różnych długości i różnych materiałów, który utwierdzono na jednym końcu (rys. 1). Uwzględniono jedynie przemieszczenia elementów pręta w kierunku poprzecznym do osi geometrycznej pręta ![]()
. Pręt poddano początkowym sprężystym ugięciom; to jest swobodny koniec obciążono siłą prostopadłą do jej osi, którą nagle usunięto (przyjęto hipotezę płaskich przekrojów).
Rys. 1. Obciążenie drgającego pręta
Stosując zasadę d'Alemberta dla elementu pręta o długości ![]()
zapisano równanie różniczkowe:
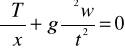
(1)
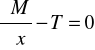
(2)
gdzie:
![]()
- przemieszczenie liniowe dowolnego elementu ![]()
o długości pręta ![]()
w kierunku poprzecznym do osi geometrycznej ![]()
,
![]()
- siła poprzeczna w kierunku pręta,
![]()
- moment tych sił względem środka długości elementu z pominięciem małych rzędu wyższego,
![]()
- siła bezwładności elementu pręta o długości ![]()
,
![]()
- moduł Younga materiału pręta,
![]()
- osiowy moment bezwładności przekroju porzecznego pręta,
![]()
- sztywność przekroju pręta na zginanie,
![]()
- długość pręta,
![]()
- czas,
![]()
- przyśpieszenie ziemskie,
![]()
- ciężar pręta przypadający na jednostkę długości ![]()
,
![]()
- oś geometryczna pręta.
Po zróżniczkowaniu równania (2) względem ![]()
i podstawieniu do (1) otrzymano
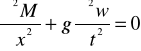
. (3)
Dla małych ugięć pręta, równanie linii ugięcia zapisano w następującej formie
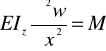
. (4)
Po dwukrotnym zróżniczkowaniu (4); ![]()
i po podstawieniu do (3) równania ruchu elementu pręta otrzymano w następującej formie
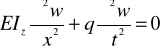
. (5)
Równanie (5) zapisano następująco
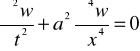
(6)
gdzie: 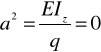
.
Rozwiązanie równania (6), po zastosowaniu metody zmiennych rozdzielonych przedstawiono w formie funkcji ![]()
w postaci iloczynu dwóch funkcji
![]()
. (7)
Po podstawieniu (6) do (7) otrzymano
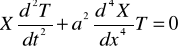
. (8)
Żeby równanie (8) było spełnione dla każdego ![]()
i ![]()
musi zachodzić związek
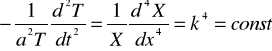
. (9)
Związek (9) jest równoważny układowi dwóch sprzężonych równań różniczkowych:
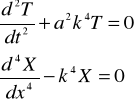
(10)
gdzie:
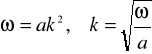
. (11)
Rozwiązanie ogólne pierwszego równania z układu równań (10) przedstawiono w formie:
![]()
(12)
gdzie: ![]()
są stałymi, które można wyznaczyć z warunków początkowych ruchu.
Rozwiązanie ogólne równania (10) zapisano następująco
![]()
(13)
gdzie: ![]()
- są stałymi, które wyznaczono z warunków brzegowych.
Dla pręta prostego ugięcie i kąt ugięcia na końcu utwierdzonym pręta oraz moment gnący i siła tnąca na końcu swobodnym są równe zeru. Warunki zapisano w następującej formie:
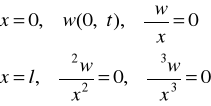
(14)
Po wykonaniu przekształceń algebraicznych ostatecznie uzyskano równanie częstości w postaci
![]()
. (15)
Równanie zostało rozwiązane wykreślnie, gdzie otrzymano wzory określające częstośći własne:
częstość podstawowa
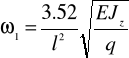
(16)
druga częstość harmoniczna
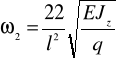
(17)
Częstością własnym (16), (17) odpowiadają postacie drgań. Ponieważ istnieje ![]()
częstość własnych to istnieje ![]()
rozwiązań szczególnych o postaci (12) i (13) układu (10).
Rozwiązaniem ogólnym równania (6) zgodnie z (7) są następujące funkcje w postaci sumy:
![]()
(18)
3. Opis stanowiska badawczego
Na stanowisku badawczym (rys. 2) znajduje się pręt jednostronnie zamocowany w specjalnym uchwycie. Przy mocnym dokręceniu śrub zaciskowych uchwytu 2 otrzymano model pręta zamocowanego jednym końcem. Uchwyt pręta pozwala na zmianę długości i materiałów pręta. Do pomiaru częstości zastosowano układ złożony z liczników cykli 3 i miernika czasu 4 [1].
Włączony układ pomiarowy wymaga zwarcia zacisków A i B. W czasie pomiaru drgający pręt zawiera zaciski czujnika 5. W zamykanym okresowo obwodzie działają trzy liczniki cykli, dzięki czemu otrzymano niezawodny pomiar liczby cykli.
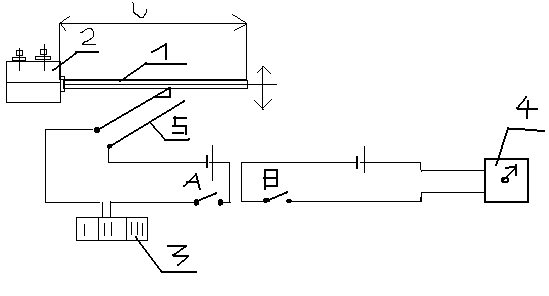
Rys. 2. Schemat układu pomiarowego
4. Przebieg ćwiczenia
Ćwiczenie polega na wykonaniu pomiarów podstawowej częstości drgań własnych tłumionych wzbudzającego pręta dla różnych długości i materiałów. Następnie obliczeniu podstawowej częstości drgań własnych nie tłumionych ze wzoru (16) dla tych samych długości ![]()
i modułów Younga ![]()
; sporządzeniu wykresów funkcji ![]()
i ![]()
, ![]()
oraz ocenie wielkości tłumienia częstości [1].
W celu pomiaru częstości drgań własnych należy wyskalować pręt, oznaczając na nim długości ![]()
i moduły Younga ![]()
podłączyć go do źródła zasilania mierników cykli i miernika czasu.
Dane liczbowe:
![]()
![]()
![]()
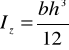
.
Po przygotowaniu stanowiska należy zamocować kolejno pręt o różnych długościach ![]()
w uchwycie stanowiska i mierzyć dla każdej długości pręta kilkakrotnie liczbę cykli ruchu w przeciągu kilku do kilkunastu sekund.
Uzyskane wyniki pomiarów należy zapisać w tablicy nr. 1
Tablica 1
długość belki |
liczba cykli wskazana przez licznik |
liczba cykli |
czas pomiaru
|
częstotliwość
|
|
|
|
|
|
|
|
|
|
|
Częstość obliczeniową wykonano w oparciu o wskazanie w tablicy nr. 2
Tablica 2
długość belki |
częstość podstawowa
|
różnica
|
|
|
|
|
|
|
|
|
|
Po przygotowaniu stanowiska należy zamocować kolejno pręt o różnych modułach Younga ![]()
w uchwycie stanowiska i mierzyć dla każdego modułu Younga pręta kilkakrotnie liczbę cykli ruchu w przeciągu kilku do kilkunastu sekund.
Uzyskane wyniki pomiarów należy zapisać w tablicy nr. 3
Tablica 3
moduł Younga belki |
liczba cykli wskazana przez licznik |
liczba cykli |
czas pomiaru
|
częstotliwość
|
|
|
|
|
|
|
|
|
|
|
Częstość obliczeniową wykonano w oparciu o wskazanie w tablicy nr. 4
Tablica 4
moduł Younga belki |
częstość podstawowa
|
różnica
|
|
|
|
|
|
|
|
|
|
Obliczona różnica w ostatniej kolumnie tablicach 2, 4 zawiera w sobie efekt tłumienia i błędy pomiarowe. Błędy pomiarowe wynikające głównie z niedokładności odmierzania długości czynnej pręta ![]()
oraz z pomiaru czasu ![]()
, który odpowiada liczbie cykli ![]()
są błędnymi przypadkowymi. Można błędy wyeliminować z określonej różnicy wyliczając wartość średnią
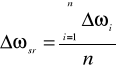
(19)
Średnia wartość z przybliżeniem określa wartość tłumienia częstości drgań spowodowanej oporami zewnętrznymi ruchu, tarciem wewnętrznym i tarciem konstrukcyjnym w miejscu zamocowania pręta.
5. Treść sprawozdania
opis stanowiska z rysunkiem
wzory obliczone z wyjaśnieniem
tabelki z wynikami pomiarów i obliczeń
wykresy funkcji
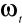
i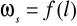
;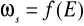
obliczenie przybliżonej wartości tłumienia częstości
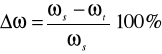
(20)
dyskusje wyników
LITERATURA
Praca zbiorowa: Wernerowski K., Siołkowski B., Holka H.: Laboratorium z kinematyki i dynamiki, WSI, Bydgoszcz 1973.
Jakowluk A.: Mechanika techniczna i ośrodków ciągłych, Ćwiczenia laboratoryjne, PWN, Warszawa 1977.
Osiński Z.: Teoria drgań, PWN, Warszawa 1978.
Wernerowski K., Topoliński A.: Zbiór zadań z kinematyki, dynamiki i drgań, Wydawnictwo Uczelniane ATR, Bydgoszcz 1984.
Botwin M.: Mechanika i wytrzymałość materiałów. PWN, Warszawa.
Bukowski J.: Mechanika płynów. PWN, Warszawa.
Jakubowicz A., Orłoś Z.: Wyrzymałość materiałów. WNT, Warszawa.
Misiak J.: Mechanika techniczna, t. 1; Statyka i wytrzymałość materiałów. WNT, Warszawa.
Siuta W.: Mechanika techniczna. WSiP, Warszawa.
Zielnica J.: Wytrzymałość materiałów. Wyd. Politechniki Poznańskiej.
8
Wyszukiwarka
Podobne podstrony:
LABOR4, Politechnika, Mechanika Techniczna, Materiały z CD, 2 Lab Skręcanie wałów kołowo symetryczny
Publikacii, Politechnika, Mechanika Techniczna, Materiały z CD, Dynamika modelowanie
PROT5, Politechnika, Mechanika Techniczna, Materiały z CD, Dynamika modelowanie
pewniaki z rozwiazaniami, Szkoła, Semestr 3, Semestr 3, Mechanika techniczna II, chomika od barta, M
dzial 10 i12 z rozwiazaniem, Szkoła, Semestr 3, Semestr 3, Mechanika techniczna II, chomika od barta
Tarcie, Materiały, Inżynieria Środowiska, Semestr 2, Mechanika techniczna, egzaminy
Maszyny-koło projekt, Technologia chemiczna, Maszynoznawstwo i mechanika techniczna, ogólne materiał
cw9inzmat, Politechnika Lubelska, Elektrotechnika inż, ROK 2, Lab. Inż Materiałowa
POMIAR TWARDOŚCI SPOSOBEM BRINELLA, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzy
Mechanika Techniczna lab 2
cw 4, Politechnika Lubelska, Elektrotechnika inż, ROK 2, Lab. Inż Materiałowa
Mechanika - 3cie kolokwium, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałość m
mechanika - teoria, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałość materiałó
6.Tensometria(3), POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałość materiałów,
Wyklady, politechnika krakowska transport niestacjonarne, semestr III, mechanika techniczna
mechanka lab, mecnika locati, LABORATORIUM MECHANIKI TECHNICZNEJ
Wytrzymałość materiałów, Wytrzymałość materiałów - dziedzina wiedzy inżynierskiej, cześć mechaniki t
więcej podobnych podstron