17 lutego 2012
Grafika Inżynierska I kolokwium Imię i Nazwisko:.............................................................
Piszemy bez korzystania z notatek! Odwrotną stronę kartki można wykorzystać jako brudnopis
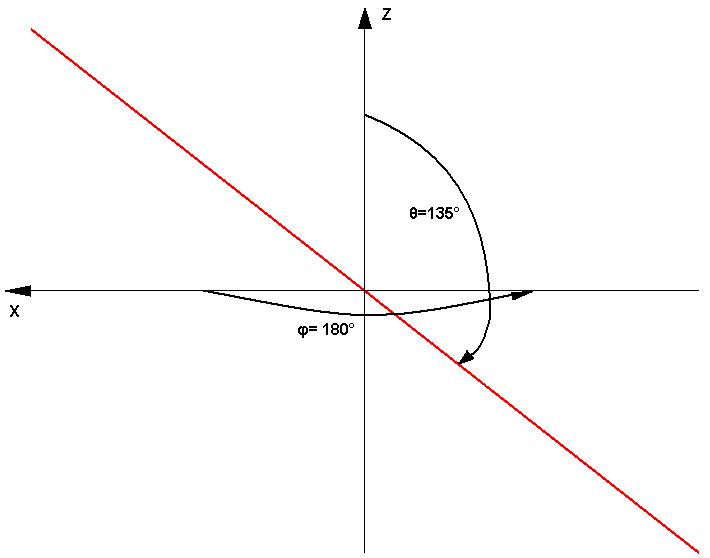
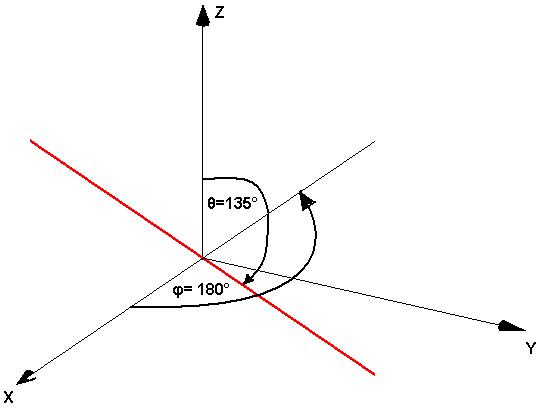
a) Naszkicuj linię w przestrzeni opisaną równaniem:
θ=135°, φ= 180°. b) Zapisz ją w prostokątnym układzie współrzędnych
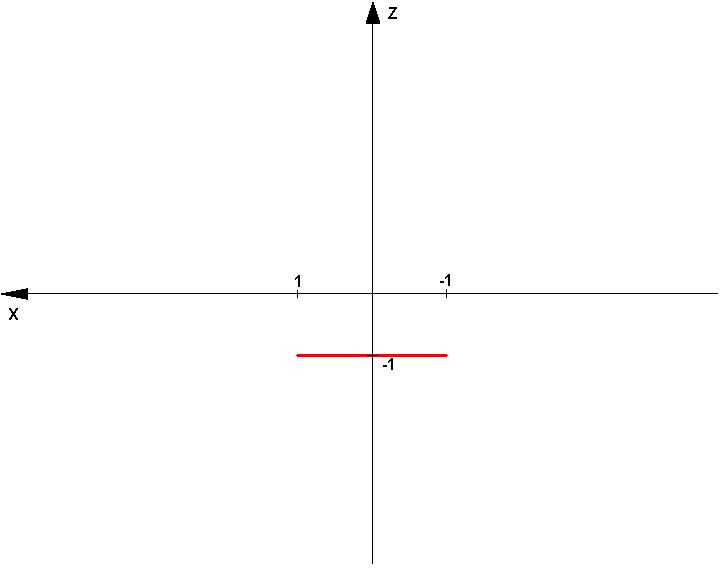
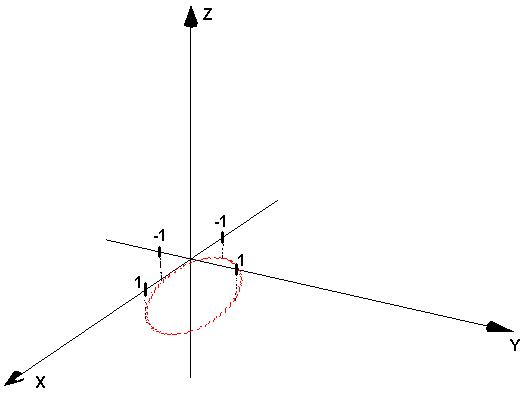
Zapisz równanie(a) opisujące krawędź przecięcia płaszczyzny równoległej do płaszczyzny xy (z = 0) i leżącej na wysokości - 1 pod nią, z pobocznicą walca o promieniu 1, która to pobocznica jest współ-osiowa z osią z, w układach:
Prostokątnym
Walcowym
Sferycznym
Sporządzić odpowiedni szkic. Odpowiedź wpisać w odpowiednią ramkę.
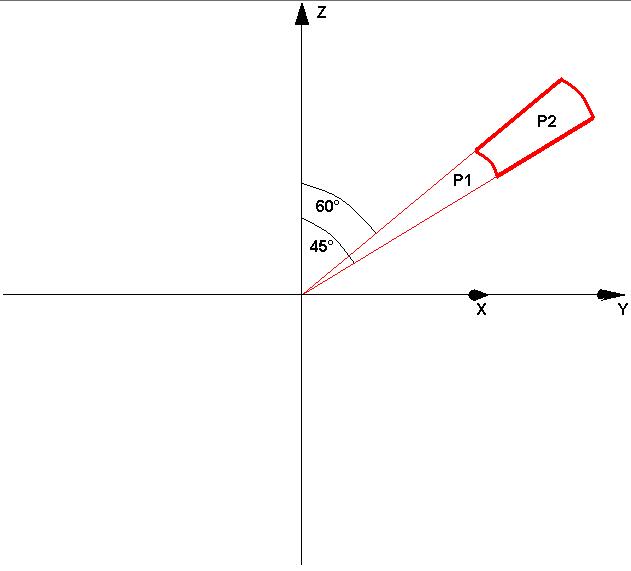
Oblicz powierzchnię obszaru (8< r , 45° < θ leżącego na półpłaszczyźnie = 30°. Całkowanie nie jest konieczne, choć przyspiesza obliczenia. (MAX=6p)
Wyprowadź zależność na współczynnik proporcjonalności pomiędzy przyrostem zmiennej a przyrostem drogi (współczynnik metryki) dla przypadku poruszania się po drodze opisanej równaniem: r =2 i θ=30°.
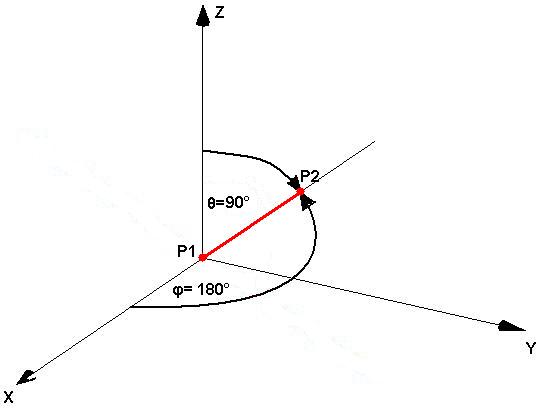
W układzie współrzędnych sferycznych dane są dwa punkty P1(0, 12°.14, 37°.45) i P2 (4, 90°, 180°). Oblicz najkrótszą odległość L pomiędzy tymi punktami. (Nie zgadywać, musi być uzasadnienie słowne lub obliczeniowe.)
Ad.1
Ad.2
Ad.3 Ad.5
Miejsce na obliczenia i szkic:
ρ=√x²+y²=√1=1
r=√x²+y²+z²=√1+1=√2
Miejsce na obliczenia i szkic:
Jeśli r1 wynosi 0 to reszta współrzędnych nie ma znaczenia.
r2-r1=4-0=4
W układzie prostokątnym: X=Z; Y=0
r=√2; Θ=135°; φ=360°
ρ=1; φ=360° Z=-1
Miejsce na obliczenia i szkic:
h=.............................
Miejsce na szkic:
L = ......4...
X²+Y²=1; Z=-1
S= ...... 10π/3....
Miejsce na obliczenia i szkic:
ro=12-8=4
60°-45°=15° Pc=πr²/24=12²π/24=144π/24=6π
360°/15°=24 P1=πr1²/24=8²π/24=64π/24=8π/3
P2=Pc-P1=6π-8π/3=10π/3