1. ESTYMATOR. POJĘCIE, WŁASNOŚCI, ZASTOSOWANIE.

Estymator T_n - określona statystyka z próby służąca oszacowaniu nieznanej wartości parametru populacji

Własności estymatorów:

1. 1. zgodność - estymator jest zgodny, jeżeli spełniony jest warunek:
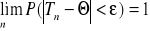
   dla dowolnie małego ε>0

2. nieobciążoność - estymator T_n parametru θ jest nieobciążony jeśli E(T_n) = θ, tzn. estymator szacuje parametr θ bez błędu systematycznego.

3. efektywność - T_n jest estymatorem najefektywniejszy, jeżeli z klasy estymatorów nieobciążonych ma on najmniejszą wariancję.

4. wystarczalność - estymator T_n jest wystarczalny jeżeli zawiera wszystkie tkwiące w próbie informacje dotyczące parametru θ

Uwagi dotyczące własności estymatorów:

1. jeżeli estymator T_n parametru θ jest zgodny, to jest asymptotycznie nieobciążony

2. jeżeli estymator T_n parametru θ jest nieobciążony oraz spełniona jest relacja
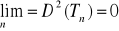
   to jest on estymatorem zgodnym

3. jeżeli estymator T_n parametru θ jest nieobciążony, to
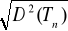
   jest średnim błędem szacunku

2. PRZEDZIAŁ UFNOŚCI, DEFINICJA, ZASTOSOWANIE

Przedział ufności - taki przedział, który spełnia warunki:

1. jego końce θ₁ = θ₁(X₁,...X_n) i θ₂ = θ₂(X₁,...X_n) są funkcjami próby losowej i nie zależą od szacowanego parametru θ

2. prawdopodobieństwo pokrycia przez ten przedział nieznanego parametru θ jest równe 1-α

3. SZACOWANIE ŚREDNIEGO POZIOMU CECHY W ZBIOROWOŚCI GENERALNEJ NA PODSTAWIE WYNIKÓW Z PRÓBY. WYBÓR ESTYMATORA W ZALEŻNOŚCI OD POSIADANYCH INFORMACJI, ROZKŁAD ESTYMATORA.

MODEL I

Założenia:

X - cecha populacji generalnej

X ~ N(μ,σ)

σ - znane

θ = μ

T_n =

~

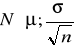
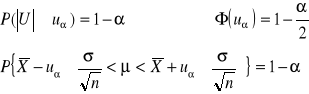
MODEL II

Założenia:

X - cecha populacji generalnej

X ~ N(μ,σ)

μ,σ - nieznane

θ = μ

T_n =

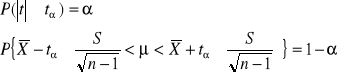
MODEL III

Założenia:

X - cecha populacji generalnej

X ~dowolny rozkład

μ,σ² - nieznane

θ = μ

T_n =

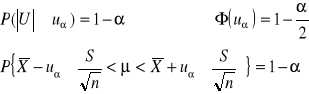
4. SZACOWANIE UDZIAŁU JEDNOSTEK Z WYRÓŻNIONYM WARIANTEM CECHY BADANEJ W ZBIOROWOŚCI GENERALNEJ W OPARCIU O WYNIKI Z PRÓBY.

Założenia:

θ = p

T_n =

~
~

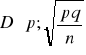
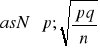
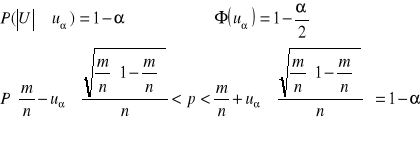
5. SZACOWANIE ROZPROSZENIA BADANEJ CECHY W ZBIOROWOŚCI GENERALNEJ. WYBÓR ESTYMATORA W ZALEŻNOŚCI OD POSIADANYCH INFORMACJI. PRZEDZIAŁY UFNOŚCI

MODEL I

Założenia:

μ,σ - nieznane

n -małe

θ = σ²

T_n = S²

~

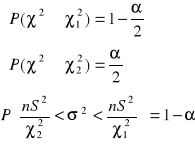
MODEL II

Założenia:

μ,σ - nieznane

n - duże

θ = σ

T_n = S

S ~ N(μ,
)

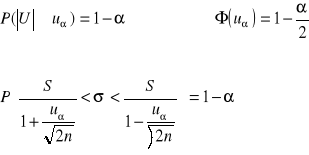
6. USTALENIE NIEZBĘDNEJ LICZEBNOŚCI PRÓBY PRZY ŻĄDANEJ WIARYGODNOŚCI I DOKŁADNOŚCI OSZACOWANIA PARAMETRÓW W ZBIOROWOŚCI GENERALNEJ

MODEL I

Założenia:

X - cecha populacji generalnej

X ~ N(μ,σ)

σ - znane

θ = μ

T_n =

1-α

Minimalną liczebność próby, niezbędną do oszacowania wartości średniej μ na poziomie ufności 1- α, z maksymalnym błędem szacunku nie przekraczającym d, obliczamy ze wzoru:
. W przypadku, gdy prawa strona nierówności nie jest liczbą całkowitą, wystarczy pobrać próbkę o liczebności

MODEL II

Założenia:

X ~ N(μ,σ)

μ,σ - nieznane

1-α

θ = μ

T_n =

n=?

n_o-dane i małe

Ponieważ wariancja S² przyjmuje różne wartości dla różnych próbek, to należy zastosować tu dwustopniowe postępowanie:

1. z populacji pobieramy próbkę wstępną o liczebności n₀ i obliczamy:
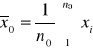
   oraz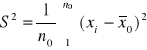
   

2. obliczamy
   

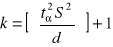
Jeżeli obliczona liczebność próby n spełnia nierówność
to liczebność n₀ próby wstępnej uważamy za wystarczającą. W przeciwnym przypadku należy zwiększyć próbę wstępną o n-n₀ elementów.

MODEL III

Minimalną liczebność próby, niezbędną do oszacowania wskaźnika struktury p na poziomie ufności 1- α, z maksymalnym błędem szacunku nie przekraczającym d, obliczamy na podstawie przedziału ufności dla estymacji parametru.

W przypadku gdy można wstępnie oszacować wartość parametru p, posługujemy się wzorem:
. Jeżeli jednak nie znamy rzędu wielkości szacowanego parametru p, to do wzoru w miejsce p₀ wstawiamy liczbę ½ i otrzymujemy wzór

7. ESTYMACJA WSPÓŁCZYNNIKA KORELACJI

Korzystanie z procedury estymacyjnej, wymaga założenia o tym, że populacja ma rozkład dwuwymiarowy normalny ze względu na badane cechy.

Założenia:

n - duże

1-α

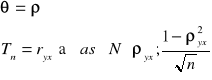
Przedział ufności dla współczynnika korelacji ma postać:

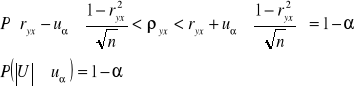
Estymacja

- 2 -

---