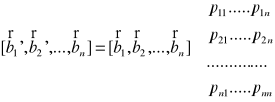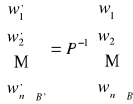WYKŁAD 6,7

WEKTORY I PRZESTRZENIE WEKTOROWE

W wykładzie omówimy definicję przestrzeni wektorowej. Przedstawimy jej podstawowe własności i przykłady, w tym przestrzenie Rⁿ. Zdefiniujemy pojęcie liniowej niezależności wektorów oraz metody jej sprawdzania.

Definicja-1 Niepusty zbiór V nazywamy rzeczywistą przestrzenią wektorową (liniową) jeśli:
1	dla każdych określona jest ich suma taka że ;
2	dla każdej liczby rzeczywistej i określony jest iloczyn taki że
Powyższe działania spełniają następujące warunki dla dowolnych
3	przemienność dodawania:
4	łączność dodawania:
5	istnienie elementu neutralnego dodawania, tj. wektora , t.że
6	istnienie elementu przeciwnego do elementu , tj. takiego, że
7	dla dowolnych
8	dla dowolnego
9	dla dowolnych
10	dla dowolnego

Zastępując w definicji rzeczywistej przestrzeni wektorowej liczby rzeczywiste α i β przez liczby zespolone otrzymamy definicję

zespolonej przestrzeni wektorowej.

Elementy przestrzeni V nazywamy wektorami oznaczamy je strzałkami.

Element neutralny
nazywamy wektorem zerowym przestrzeni V.

Dla operacji wprowadzonych w przestrzeni liniowej łatwo uzasadnić następujące własności:

Stwierdzenie:
11	dla każdego ;
12	dla każdego ;
13	, gdy ;
14	, gdy
15
16

Definicja-2 (ogólniejsza)

Przestrzeń liniowa (wektorowa) V nad ciałem K to struktura składająca się ze zbioru V którego elementy nazywamy wektorami oraz z ciała liczbowego (K,+,•) i działań oraz gdzie : nazywamy dodawaniem wektorów ze zbioru V nazywamy mnożeniem wektora ze zbioru V przez liczbę z ciała K

Działania te mają następujące własności:

Struktura jest grupą przemienną (abelową)
1		działanie wewnętrzne
2		działanie łączne
3		istnienie elementu neutralnego
4		istnienie elementu symetrycznego
5		działanie przemienne
W strukturze okreslono mnożenie wektora przez liczbę z ciała K
6	działanie wewnętrzne
III. Działania spełniają warunki zgodności
7		rozdzielność
8		rozdzielność
9		łączność
10		przeniesienie jedynki

Wprowadzimy jeszcze pojęcie podprzestrzeni wektorowej czyli przestrzeni wektorowej zanurzonej w danej przestrzeni wektorowej.

Definicja
Niepusty podzbiór W V jest podprzestrzenią liniową, jeśli spełnione są 2 warunki:
1
2

Innymi słowami działania:

• dodawania wektorów

• mnożenia wektora przez liczbę

są wewnętrzne w podzbiorze W

(nie wyprowadzają poza podzbiór W)

Przykłady przestrzeni wektorowych

Podstawowym przykładem przestrzeni liniowej jest

rzeczywista przestrzeń n-wymiarowa Rⁿ :

Działania w
są określone następująco:

gdzie:
i

W szczególności przestrzeń R³ możemy utożsamiać ze zbiorem trójek liczb rzeczywistych [x₁,x₂,x₃], które odpowiadają współrzędnym wektorów

w pewnym wybranym układzie współrzędnych.

Kartezjański układ współrzędnych w

• Początek układu, np. punkt
  .

• Trzy wzajemnie prostopadłe proste poprowadzone przez punkt
  - osie x, y, z układu.

• Jednostki długości określone na każdej osi.

• Współrzędne
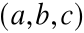
  punktu P - rzuty punktu P kolejno na osie x, y, z.

y

• P(a,b,c)

x

(0, 0, 0)

z

Wektory przestrzeni wektorowej R³ zadane za pomocą trójek liczb
możemy również utożsamiać ze skierowanym odcinkiem o początku w punkcie

i końcu w punkcie
.

Podobnego utożsamienia możemy dokonać w dowolnej przestrzeni Rⁿ.

Przykłady innych przestrzeni liniowych:

1. Przestrzeń A_mxn macierzy o m wierszach i n kolumnach. Operacje dodawania i mnożenia w tej przestrzeni pokrywają się z poznanymi przez nas poprzednio operacjami na

macierzach:

,

,

gdzie
,

2. Przestrzeń R[x]

zbiór wszystkich wielomianów rzeczywistych

3. Przestrzeń

zbiór wielomianów rzeczywistych stopnia ≤ n

4. Przestrzeń funkcji T(I) określonych na przedziale
   . Działania w przestrzeni T(I) wprowadzamy w sposób naturalny:

f+g

0.5

g f

0 1

Kombinacja liniowa wektorów

Definicja

Kombinacją liniową wektorów , i = 1, 2, ...,n nazywamy wektor postaci gdzie , i =1, 2, ... , n są liczbami rzeczywistymi

Przykład (przestrzeń
)

[4, 5, -8] = 1∙[0, 1, 0] + 2[2, 2, -4]

4[1, 2, 3] + 5[-3, 4, 2] - 4[1, 0, 1] =[-15, 28, 18]

Definicja

Zbiór wszystkich kombinacji liniowych ustalonych wektorów dla dowolnych nazywamy przestrzenią liniową rozpiętą na wektorach i oznaczamy przez symbol lin{ }. Wektory nazywamy wektorami generującymi lub generatorami przestrzeni lin{ }.

Przykład - Przestrzeń R³

Podprzestrzeń rozpięta na wektorach
i
ma postać kombinacji wektorów o współczynnikach rzeczywistych:

i wyznacza płaszczyznę w przestrzeni przechodzącą przez punkt
w której wektory [4,3,1] i [1,2,0] są zawarte.

Przestrzeń liniowa rozpięta na zbiorze wektorów jest przykładem podprzestrzeni liniowej.

Definicja

Skończony ciąg wektorów jest liniowo niezależny wtedy i tylko wtedy gdy : dla każdego układu liczb rzeczywistych takich że: zachodzi: albo mówiąc krócej - zachodzi implikacja:

Nieskończony ciąg wektorów jest liniowo niezależny, gdy każdy jego skończony podzbiór jest liniowo niezależny.

Jeżeli wektory nie są liniowo niezależne, to mówimy, że są one liniowo zależne

Przykład

Jeżeli jeden wektor jest liniowo zależny to istnieje liczba taka że a z tego wynika że czyli jest wektorem zerowym

Jeżeli dwa wektory są liniowo zależne, to istnieją liczby gdzie , takie, że Jeśli np. to wtedy: czyli jest proporcjonalny do (wektory te są wpółliniowe)

Jeżeli trzy wektory są liniowo zależne, to istnieją takie, że lub lub oraz Jeżeli np. to czyli wektor jest liniową kombinacją pozostałych wektorów. (wektory te są współpłaszczyznowe)

Stwierdzenie

Dwa wektory w przestrzeni R^2 są liniowo niezależne wtedy i tylko wtedy gdy nie są współliniowe

Trzy wektory w przestrzeni R^3 są liniowo niezależne wtedy i tylko wtedy gdy nie są współpłaszczyznowe.

Twierdzenie Układ wektorów jest liniowo zależny wtedy i tylko wtedy, gdy jeden spośród wektorów jest liniową kombinacją pozostałych

Przykład - Przestrzeń R³

Wektory [1, 2, 3], [-3, 4, 2], [1, 0, 1] , [-15, 28, 18]

są liniowo zależne, można bowiem zauważyć że:

4[1, 2, 3] + 5[-3, 4, 2] - 4[1, 0, 1] = [-15, 28, 18]

Przykład - Przestrzeń T(I)

Funkcje
i
są liniowo niezależne w przestrzeni T[0,2π] natomiast funkcje
,
i
nie są liniowo niezależne,

gdyż
dla x
[0,2π]

Z definicji liniowej niezależności wynikają następujące fakty:
1	wektor jest liniowo niezależny wtedy i tylko wtedy gdy
2	podzbiór zbioru liniowo niezależnych wektorów jest liniowo niezależny
3	jeśli wektory są liniowo zależne to zbiór wektorów jest również liniowo zależny dla dowolnego ;
4	Zbiór jest zawsze liniowo zależny dla dowolnych

Liniowa niezależność wektorów w Rⁿ

Przypomnijmy, że wektory
są liniowo niezależne wtedy i tylko wtedy, gdy macierz A o kolumnach
wymiaru n x k ma rząd k.

Zauważmy, że wówczas z tw. Kroneckera-Capelli wynika, że równanie
ma dokładnie jedno

rozwiązanie i jest to rozwiązanie zerowe
.

Ostatnie stwierdzenie jest niczym innym tylko

definicją liniowej niezależności!

Wykorzystując jeszcze raz tw. Kroneckera-Capelli możemy stwierdzić, że maksymalna liczba liniowo niezależnych wektorów w przestrzeni
wynosi n.

Twierdzenie

Żaden układ
wektorów z

nie jest liniowo niezależny.

Dowód

Macierz
ma wymiar (n)
(n+1),

a zatem nie może mieć rzędu równego n+1.

Twierdzenie

Układ wektorów
o wymiarze n jest liniowo niezależny wtedy i tylko wtedy gdy:

Przykład

Sprawdzić, czy wektory są liniowo niezależne:

[1, 2, 3], [2, 3, 4], [3, 4, 5]

Wektory dane układamy jako wiersze macierzy A

i badamy czy rząd macierzy A jest równy 3.

A =

Det A = 0
R(A) ≠ 3 tzn. wektory są liniowo zależne.

Przykład

Wektory postaci:
i=1,2,...,n

gdzie jedynie i- ta współrzędna ≠0, są liniowo niezależne.

Oczywiście, w tym przypadku A=I a zatem
.

Wprowadzimy teraz definicję bazy przestrzeni wektorowej.

Definicja Bazą przestrzeni wektorowej V nazywamy zbiór wektorów tej przestrzeni, taki że: (1) B generuje całą przestrzeń V tj. lin{ B} = V (2) B składa się z wektorów liniowo niezależnych

Przykład

Sprawdzić, że układ wektorów

jest bazą w przestrzeni R².

Warunek (1) jest spełniony, gdyż dla dowolnego
istnieje rozwiązanie równania:

mającego postać równoważną

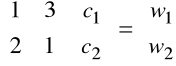
Wynika to oczywiście z faktu, że wyznacznik macierzy współczynników równania jest różny od 0.

Podobnie, aby sprawdzić warunek (2) wystarczy rozpatrzeć wektor
.Wówczas jedynym rozwiązaniem układu równań jest [c₁,c₂ၝ = ၛ0,0ၝ, a zatem układ
jest układem wektorów liniowo niezależnych.

Spełnione są warunki (1) (2) - rozpatrywany układ jest bazą.

Z przykładu wynika następujące ważne stwierdzenie:

Stwierdzenie

Niech oznacza macierz nxn taką, że j-tą kolumną tej macierzy jest wektor . Jeśli wyznacznik macierzy jest niezerowy tzn. det A≠0, to układ jest bazą przestrzeni R^n.

Udowodnimy teraz ważne twierdzenie o jednoznaczności przedstawienia wektora w bazie

Twierdzenie

Niech wektory będą bazą przestrzeni liniowej V. Każdy wektor z tej przestrzeni jest jednoznaczną kombinacją liniową wektorów tzn. w reprezentacji: współczynniki kombinacji liniowej są wyznaczone jednoznacznie i nazywają się współrzędnymi wektora w bazie

Reprezentację
wektora w bazie B zapisujemy:

Dowód:

Z definicji bazy wynika, że wektor
jest pewną kombinacją liniowa wektorów
.

Załóżmy, że wektor
posiada dwie różne reprezentacje w tej samej bazie, tzn.:

gdzie

Wówczas:

i nie wszystkie współczynniki są zerowe, co przeczy liniowej niezależności wektorów
.

Zauważmy, że dla przestrzeni Rⁿ możemy podać inny dowód tego twierdzenia.

Z twierdzenia Cramera wynika bowiem, że układ równań:

ma dokładnie jedno rozwiązanie.

Baza w przestrzeni
- układ n wektorów liniowo niezależnych.

Baza kanoniczna w przestrzeni
:

gdzie:

...

y

x

z

Każdy wektor
jest reprezentowany w bazie kanonicznej jako:

Przykład - przestrzeń R³

[-15, 28, 18] = 4[1, 2, 3] + 5 [-3, 4, 2] - 4[1, 0, 1] zatem wektor [-15, 28, 18] ma współrzędne
w bazie B={ [1, 2, 3], [-3, 4, 2], [1, 0, 1]}

Przykład

Znaleźć współrzędne wektora:

w bazie złożonej z wektorów:

w

Oznaczamy szukane współrzędne przez x, y, z;

muszą one spełniać równanie:

x[1, 1, 0] + y[1, 0, 1] + z [0, 1, 1] = [-1, -2, 3]

a zatem: x + y = -1; x + z = -2; y + z = 3

skąd: x = -3, y = 2, z = 1

Przykład : przestrzeń R³

Wektor
ma współrzędne [2, 1, -3] w bazie złożonej

z wektorów [2, 3, 0], [4, 2, 3], [1, 1, 1].

Obliczyć współrzędne wektora
w bazie

[4, 0, 1], [0, 2, 3], [2, 1, 0].

Oznaczamy szukane współrzędne przez x, y, z

2[2, 3, 0] + [4, 2, 3] -3 [1, 1, 1] =

= x [4, 0, 1] + y[0, 2, 3] + z[2, 1, 0]

Otrzymujemy układ trzech równań z 3 niewiadomymi:

4x + 2z = 5

2y + z = 5

x + 3y = 0

Postać macierzowa układu:

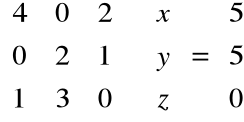
Jest to układ Cramera, gdyż wyznacznik macierzy głównej układu jest różny od zera, a zatem z twierdzenia Cramera rozwiązanie jest postaci

x =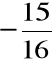
, y =
, z =

Podsumowanie

Jeżeli współrzędne wektora
∈ R³ w kolejnych bazach wynoszą odpowiednio:

[x₁, x₂, x₃] w bazie

[y₁, y₂, y₃] w bazie

[z₁, z₂, z₃] w bazie

Wtedy:

Przytoczymy jeszcze twierdzenie o równoliczności baz.

Twierdzenie

Jeśli jakakolwiek baza przestrzeni liniowej V składa się z n wektorów to każda inna baza v składa się również z n wektorów

Twierdzenie to pozwala zdefiniować wymiar przestrzeni liniowej ( ilość wektorów bazy ).

Definicja Niech zbiór wektorów będzie bazą przestrzeni V. Wówczas mówimy, że wymiar przestrzeni V wynosi n i piszemy dim( V )=n.

Przykład

Wymiar jednoelementowej przestrzeni wektorowej zawierającej tylko wektor zerowy jest równy zero

tzn.

Przykład

Wymiar przestrzeni Rⁿ wynosi n tzn.

Podprzestrzeń liniowa R² składająca się z wektorów [x,y] dla których y= -x ma wymiar 1.

Wymiar przestrzeni macierzy M_3x4 wynosi 12.

Uwaga

Istnieją przestrzenie liniowe nieskończenie wymiarowe. Na przykład w przestrzeni B(I) funkcje f_i(x) = xⁱ są liniowo niezależne dla i=0,1,2,... , zatem przestrzeń ta nie jest skończenie wymiarowa.

Wówczas piszemy

Dysponując współrzędnymi układu wektorów
w dowolnej bazie
możemy łatwo sprawdzić ich liniową niezależność.

Stwierdzenie

Niech dla 1 i k będą współrzędnymi wektora w bazie B. Wówczas są liniowo niezależne R(A) = k

Przykład

Współrzędne wektorów
w bazie

B={ၛ1,0,0ၝ, ၛ1,1,0ၝ, ၛ1,1,1ၝ} wynoszą odpowiednio:

[2, 5, -1] [-1, 2, 3] [-5,-1, 2]

Sprawdzić, czy wektory
są liniowo niezależne.

Macierz współrzędnych wektorów ma postać:

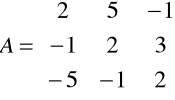
Stwierdzamy, że detA = - 62 ≠ 0 zatem R(A)=3

A więc wektory
są liniowo niezależne.

Rozpatrzmy przestrzeń liniową V wymiaru n i niech:

będą dwiema różnymi bazami przestrzeni V.

Zapiszmy wektory nowej bazy B' jako kombinacje liniowe wektorów starej bazy B o współczynnikach p_ij:

...................................................

Definicja

Macierzą przejścia od bazy B do bazy B' nazywamy macierz P= [p_ij], której kolejnymi kolumnami są współrzędne kolejnych wektorów bazy B' w bazie B.

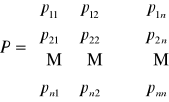
Przykład - Przestrzeń R³

jest bazą kanoniczną

B' =
={[1,0,0],[1,1,0],[1,1,1]}

Wówczas macierz przejścia od bazy B do B' ma postać

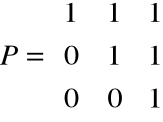
Zatem w przypadku gdy B jest bazą kanoniczną w przestrzeni Rⁿ, macierz przejścia od bazy kanonicznej do dowolnej bazy B' składa się z wektorów tej bazy ustawionych w kolumnach.

Wyraźmy teraz wektory bazy kanonicznej przez wektory
:

Zatem odpowiednia macierz przejścia od bazy B' do bazy B

ma postać

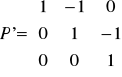
i jak łatwo sprawdzić:
.

Jest to przypadek szczególny następującego stwierdzenia.

Stwierdzenie

Jeśli P jest macierzą przejścia od bazy B do bazy B', to: P jest macierzą odwracalną tzn. istnieje P ^-1 P ^-1 jest macierzą przejścia od bazy B' do bazy B.

Stwierdzenie

Jeśli współrzędne wektora w bazie B są równe w1,...,wn to jego współrzędne w1',...,wn' w bazie B' spełniają równanie: gdzie P jest macierzą przejścia od bazy B do bazy B'.

Przykład cd.

Współrzędne wektora
w bazie B' mają postać

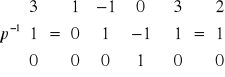
Zatem

Przestrzeń rozwiązań układu równań jednorodnych

Niech A=[a_ij] będzie macierzą mxn rzędu k i rozpatrzmy układ jednorodny równań liniowych

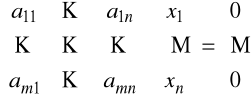
Niech S⊂ Rⁿ będzie zbiorem wszystkich wektorów
będących rozwiązaniem układu jednorodnego.

Stwierdzenie

S jest podprzestrzenią liniową wymiaru n-k

Podobnie, dla układu niejednorodnego

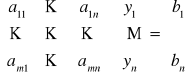
Niech T będzie zbiorem rozwiązań tego układu i niech
będzie dowolnym wektorem z T.

Stwierdzenie

Dla każdego ∈ T zachodzi

Ze stwierdzenia wynika zatem, że wszystkie rozwiązania układu niejednorodnego otrzymujemy dodając do szczególnego rozwiązania tego układu wszystkie rozwiązania układu jednorodnego.

W szczególności, dla układu trzech równań zbiór rozwiązań może być zbiorem pustym, punktem, prostą lub płaszczyzną.

Przykład

Rozpatrzmy układ równań:

2x + 3 y + 2z = 7

x + y + 2z = 4

Stosując metodę eliminacji Gaussa stwierdzamy, że zbiorem rozwiązań układu jednorodnego są wektory postaci:

[-4z, 2z, z] dla z ∈ R.

Łatwo sprawdzić, że wektor [1,1,1] jest rozwiązaniem układu niejednorodnego. Zatem ogólne rozwiązanie układu niejednorodnego ma postać:

[-4z + 1, 2z + 1, z + 1] dla z ∈ Rⁿ.

Algebra Liniowa z Geometrią

3

---