Piotr Kucab Rzeszów, 18.03.2008 r.
I BD, LP6
|
POLITECHNIKA RZESZOWSKA
WYDZIAŁ BUDOWNICTWA I INŻYNIERII ŚRODOWISKA KATEDRA FIZYKI |
Laboratorium z fizyki
Ćw. 8 Pomiar momentu bezwładności koła Maxwella
I. Wymagania do ćwiczenia:
II zasada dynamiki - Jeśli siły działające na ciało nie równoważą się (czyli siła wypadkowa F jest różna od zera), to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej
Współczynnik proporcjonalności jest równy odwrotności masy ciała.
Energia kinetyczna - to energia ciała, związana z jego ruchem. Dla ciała o masie m i prędkości v<<c, gdzie c jest prędkością światła w próżni, energia kinetyczna wynosi:
Energia ruchu obrotowego ciała wynosi, w przybliżeniu małych prędkości oraz modelu bryły sztywnej:
,
gdzie
jest prędkością kątową (pseudowektor), natomiast
jest tensorem momentu bezwładności. W przypadku obrotu wokół jednej z osi głównych wyrażenie na energię kinetyczną w ruchu obrotowym upraszcza się do:
.
gdzie I jest odpowiednim momentem bezwładności, a ω prędkością kątową.
Energia potencjalna - energia jaką posiada układ ciał umieszczony w polu sił zachowawczych, wynikająca z rozmieszczenia tych ciał. Równa jest pracy, jaką trzeba wykonać, aby uzyskać aktualne rozmieszczenia ciał, wychodząc od innego rozmieszczenia, dla którego umownie przyjmuje się jej wartość równą zero. Podobnie jak pracę, energię potencjalną mierzy się w dżulach [J].
Zasada zachowania energii - w układzie izolowanym suma składników wszystkich rodzajów energii całości (suma energii wszystkich jego części) układu jest stała (nie zmienia się w czasie).
II. Metodologia wykonania ćwiczenia:
Celem ćwiczenia jest wyznaczenie momentu bezwładności koła Maxwella na podstawie doświadczenia. Koło Maxwella jest bryłą sztywną składającą się z krążka o promieniu rk, pierścienia o promieniu rp zamocowanych na osi o średnicy d. Ruch postępowy koła odbywa się pod wpływem wypadkowej siły F= mg - 2N a ruch obrotowy pod wpływem momentu sił i naciągu nici M=2rN. Moment bezwładności koła I jest liczony względem osi obrotu przechodzącej przez jego środek masy.
Ostatecznie wyrażenie na moment bezwładności koła Maxwella przyjmuje postać:
![]()
Obliczanie momentu bezwładności koła Maxwella na podstawie definicji polega na sumowaniu momentów bezwładności poszczególnych jego elementów którymi są: oś, osadzony na niej krążek oraz wymienialny pierścień.
![]()
III. Metodologia wykonywania pomiarów:
Zmierzyc średnice r oraz wysokośc h.
Odczytać wartości mas zapisanych na odpowiednich elementach. Włączyć przyrząd przyciskiem W3.
Na krążek nałożyć dowolnie wybrany pierścień.
Nawinąć na oś koła nić i unieruchomić wciskając przycisk W2.
Sprawdzić czy dolna krawędź pierścienia pokrywa się z zerem.
Wyzerować zegar przyciskiem W1. Wcisnąć przycisk W2.
Odczytać zmierzona wartość czasu spadania koła.
Pomiar wykonać co najmniej 10 razy.
IV. Tabela pomiarowa:
m0 |
mk |
m d |
d |
r0 |
rk |
rp |
r |
h |
t |
I |
It |
[g] |
[g] |
[g] |
[mm] |
[mm] |
[mm] |
[mm] |
[mm] |
[mm] |
[s] |
[kgm2] |
[kgm2] |
32,5 |
124 |
258,8 |
11 |
5 |
43 |
52,5 |
5,25 |
410 |
2,222 |
0,0198 |
0,0007124 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,212 |
0,0198 |
0,0007124 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,219 |
0,0198 |
0,0007124 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,216 |
0,0198 |
0,0007124 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,215 |
0,0198 |
0,0007124 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,221 |
0,0198 |
0,0007124 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,216 |
0,0198 |
0,0007124 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,211 |
0,0198 |
0,0007124 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,222 |
0,0198 |
0,0007124 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,213 |
0,0198 |
0,0007124 |
|
|
|
|
|
|
|
|
tśr |
2,217 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32,5 |
124 |
389,1 |
11 |
5 |
43 |
52 |
5,25 |
410 |
2,294 |
|
0,001 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,290 |
|
0,001 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,286 |
|
0,001 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,228 |
|
0,001 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,290 |
|
0,001 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,292 |
|
0,001 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,307 |
|
0,001 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,230 |
|
0,001 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,300 |
|
0,001 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
2,304 |
|
0,001 |
|
|
|
|
|
|
|
|
tśr |
2,282 |
|
|
V. Obliczenia:
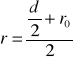
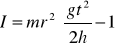
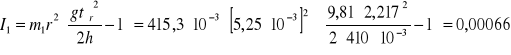
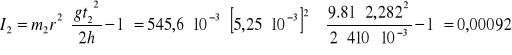
I = Io + Ik + Ip
![]()
![]()
![]()
![]()
I = Io + Ik + Ip
![]()
![]()
![]()
![]()
Niepewności typu B:
![]()
![]()
![]()
![]()
Niepewnośc typu A:
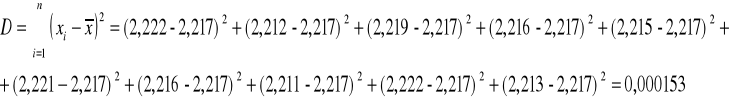
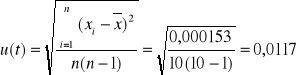
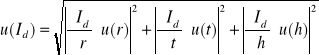
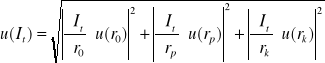
Wyszukiwarka
Podobne podstrony:
kationy, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organiczna
Reakcje Hydrolizy, II Rok WIMiC inżynieria materiałowa AGH, Chemia, Chemia -, Chemia - Laborki
Sprawozdanie 5 GIG B, II Rok WIMiC inżynieria materiałowa AGH, Chemia, Chemia -, Chemia - Laborki, S
Chemia laborka 6 zapłon
iloslab, II Rok WIMiC inżynieria materiałowa AGH, Chemia, Chemia -, laborki
Chemia mat. bud, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, 1sem.chemia.laborki, Chemi
Skutki kształtu płatu siedliska na Łuszczyka indygo, ! UR Towaroznawstwo, I ROK, Chemia, Chemia - la
sciaga na egzmin, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, 1sem.chemia.laborki
sprawko z osadów, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organic
6!!!!!!!!!, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki
hydroliza, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, 1sem.chemia.laborki, Chemia - I
Sprawozdanie 4 GIG B chemia labor, II Rok WIMiC inżynieria materiałowa AGH, Chemia, Chemia -, Chemia
CHEMIA LABORKI !
gielda chemia laborki semin
sprawko cw1, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organiczna
sprawozdanie z cw 4, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie orga
Odczyn roztworów wodnych soli, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogoln
redoksy part1, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organiczna
Badanie substancji błonotwórczych, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, 1sem.che
Cw12 Rozdzial przez stracanie, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogoln
więcej podobnych podstron