Wydział Elektroniki Politechniki Wrocławskiej	Laboratorium miernictwa elektronicznego
^Wykonał Pirosz Paweł		^Grupa 6	^Ćw. nr 2	^Prowadzący mgr R. Szczepanowski
Statystyczna analiza wyników pomiarów		^Data wykonania 98.04.07	^Data oddania 98.04.21	^Ocena

CEL ĆWICZENIA:

Celem ćwiczenia jest zapoznanie się ze statystyczną analizą wyników pomiarów, a w szczególności: sposobami znajdowania i eliminacji wyników pomiarów obarczonych błędami grubymi, wyznaczania i analizy składowej przypadkowej oraz składowej systematycznej błędów pomiarów.

WYKAZ PRZYRZĄDÓW :

• suwmiarka elektroniczna

• trójkąt nr 11

PRZEBIEG ĆWICZENIA :

Pomiar boków a, b, c i wysokości h_a, h_b, h_c trójkąta za pomocą suwmiarki elektronicznej.

ANALIZA WYNIKÓW POMIARÓW:

Błąd graniczny pojedynczego pomiaru x określa się wzorem x = 3s, gdzie s jest odchyleniem standardowym pojedynczego pomiaru.

Analizując wyniki bezpośrednich pomiarów boków i wysokości trójkąta można zauważyć, że mamy do czynienia z błędem grubym w 8 pomiarze boków a, b, c trójkąta. Rezultaty pomiarów obarczonych błędami grubymi odrzucamy, a pomiary powtarzamy. Przyjmuję więc jako wartość pomiaru 8 średnią arytmetyczną pozostałych 10 pomiarów boków trójkąta, które wynoszą: a = 94,18 mm; b = 85,16 mm; c = 76,07 mm. Pomiary wysokości trójkąta nie są obarczone błędem grubym. Zatem tabela pomiarów boków i wysokości trójkąta ma postać:

Student	a	b	c	ha	hb	hc
	[ mm ]	[ mm ]	[ mm ]	[ mm ]	[ mm ]	[ mm ]
1	94,22	85,13	76,06	65,13	72,36	81,41
2	94,18	85,17	76,09	65,38	72,35	80,59
3	94,23	85,18	76,08	65,15	72,18	80,85
4	94,15	85,17	76,05	66,59	72,18	80,97
5	94,18	85,19	76,11	65,23	72,25	80,91
6	94,15	85,17	76,08	65,19	72,25	80,88
7	94,21	85,16	76,07	65,18	72,24	80,86
8	94,18	85,16	76,07	65,18	72,18	80,84
9	94,23	85,19	76,10	65,34	72,21	80,91
10	94,08	85,10	76,03	65,15	72,17	80,41
11	94,14	85,13	76,01	65,14	72,22	80,91
m	94,177	85,159	76,068	65,332	72,235	80,867
s	0,0456	0,0281	0,0296	0,4249	0,0659	0,2445

Dla wyników z tabeli można obliczyć wartość średnią danego boku lub wysokości ze wzoru:

(1)
, gdzie i = 0,1,...,11

oraz odchylenie standardowe pojedynczego pomiaru ze wzoru:

(2)

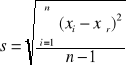
Wartości wyliczone w taki sposób podano w powyższej tabeli.

Następnie wyliczymy odchylenie standardowe średniej arytmetycznej dla boków a, b, c i wysokości h_a, h_b, h_c trójkąta ze wzoru:

(3)

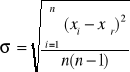
dla boku a: σ = 0,0138 mm

dla boku b: σ = 0,0085 mm

dla boku c: σ = 0,0089 mm

dla wysokości h_a: σ = 0,1281 mm

dla wysokości h_b: σ = 0,0199 mm

dla wysokości h_c: σ = 0,0737 mm

Tabela z polami trójkąta po uwzględnieniu poprawek ma zatem postać:

Student	Pa	Pb	Pc	Ph
	[ mm^2 ]	[ mm^2 ]	[ mm^2 ]	[ mm^2 ]
1	3068,3	3080,0	3096,0	3066,3
2	3078,7	3081,0	3066,0	3067,7
3	3069,5	3074,1	3075,5	3068,4
4	3134,7	3073,8	3078,9	3065,9
5	3071,7	3077,5	3079,0	3068,8
6	3068,8	3076,8	3076,7	3066,9
7	3070,3	3076,0	3075,5	3067,3
8	3069,3	3073,4	3074,7	3066,8
9	3078,5	3075,8	3078,6	3069,3
10	3064,7	3070,8	3056,8	3062,4
11	3066,1	3074,0	3075,0	3063,5
m	3076,4	3075,8	3075,7	3066,7
s	19,8	3,0	9,5	2,1

Odchylenie standardowe dla pola wyliczone ze wzoru (3) wynosi:

dla P_a: σ = 6,0 mm

dla P_b: σ = 0,9 mm

dla P_c: σ = 2,9 mm

dla P_h: σ = 0,6 mm

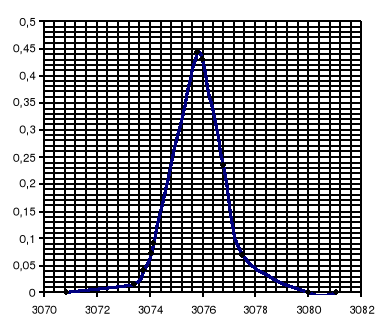
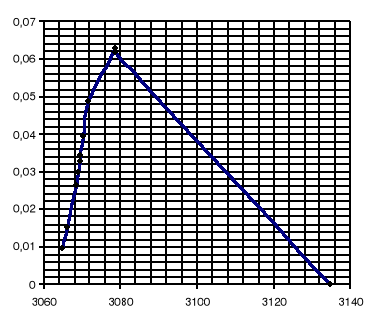
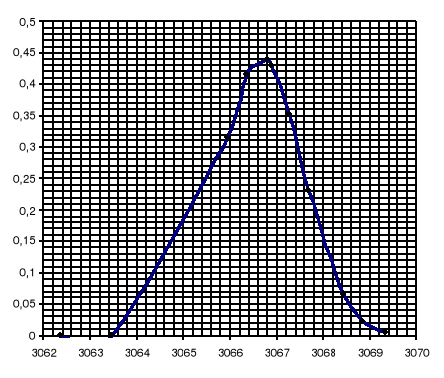
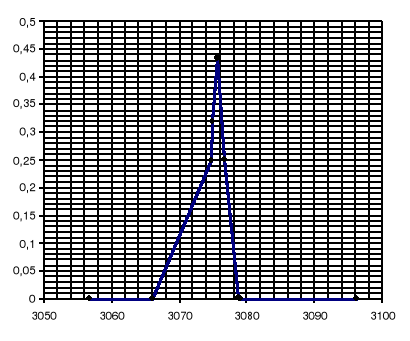
Mając wyliczone odchylenie standardowe σ dla pola trójkąta można narysować funkcję rozkładu normalnego:

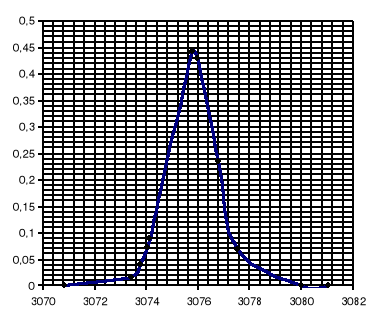
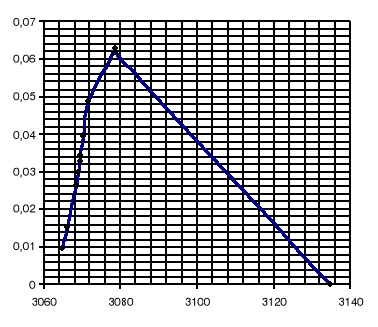
dla P_a: dla P_b:

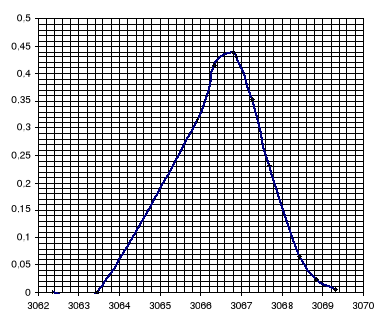
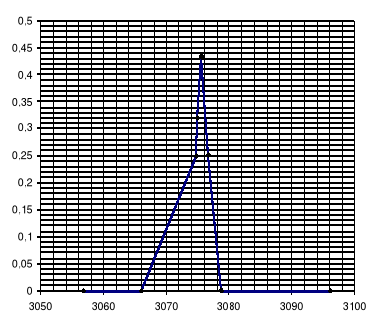
dla P_c: dla P_h:

Miara błędów przypadkowych jest wynikiem jakości i sposobu dokonywania pomiarów. Błędy te są spowodowane przez wykonującego pomiar. Mogą powstać w przypadku, gdy suwmiarka nie będzie przyłożona równolegle do krawędzi mierzonej długości boku lub gdy kąt między bokiem trójkąta a ramieniem suwmiarki będzie różny od 90°.

Analizując odchylenia standardowe poszczególnych pomiarów boków i wysokości trójkąta widzimy, że największą wartość przyjmuje ono dla pomiaru wysokości h_a i h_c. Pociąga to za sobą największą wartość odchylenia standardowego dla pola P_a i P_c, liczonych ze wzorów P_a=0,5⋅a⋅h_a, P_c=0,5⋅a⋅h_c. Można zauważyć, że odchylenie standardowe dla pola liczonego ze wzoru Herona
, gdzie
jest najmniejsze. Podobnie jest też z wartością pola: jest ona najmniejsza dla wzoru Herona. Wartości pola liczone ze wzoru P=0,5⋅a⋅h, są do siebie zbliżone. Dzieje się tak dlatego, że wartość błędu pola jest uzależniona od wartości błędu boku i wysokości. Aby to sprawdzić policzmy wartość błędu metodą różniczki zupełnej, przyjmując wartość średnią jako długość boku lub wysokości oraz σ jako błąd pomiaru długości boku lub wysokości:

Otrzymujemy więc:

P_a = 6,4 mm

P_b = 1,1 mm

P_c = 3,1 mm

Podobnie możemy obliczyć błąd dla pola liczonego ze wzoru Herona, jednak ze względu na skomplikowane obliczenia nie będę tego robił.

Widzimy zatem, że wartości błędu dla pola liczonego ze wzoru „połowa boku razy wysokość” są podobne, jak te otrzymane jako odchylenie standardowe dla wartości średniej. Widzimy więc, że mimo dość skomplikowa­nego wzoru najdokładniej wartość pola trójkąta odzwierciedla wzór Herona.

Przyjmując jako P wartość odchylenia standardowego σ możemy zapisać wartości poszczególnych pól trójkąta:

P_a = 3076,4 ± 6,0 [mm²]

P_b = 3075,8 ± 0,9 [mm²]

P_c = 3075,7 ± 2,9 [mm²]

P_h = 3066,7 ± 0,6 [mm²]

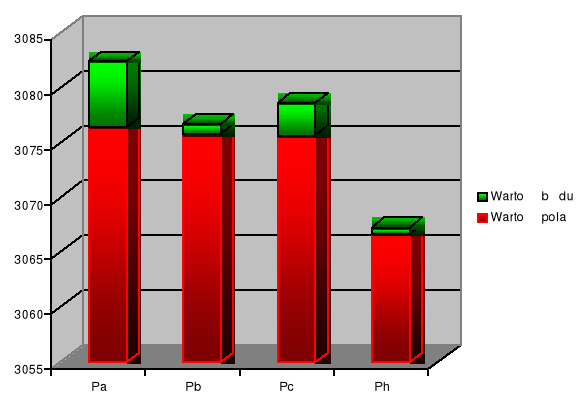
Na poniższym wykresie przedstawiono wartości pola trójkąta wyliczane ze wzoru „połowa boku razy wysokość” i wzoru Herona. Wykres ten potwierdza nasze teoretyczne rozważania.

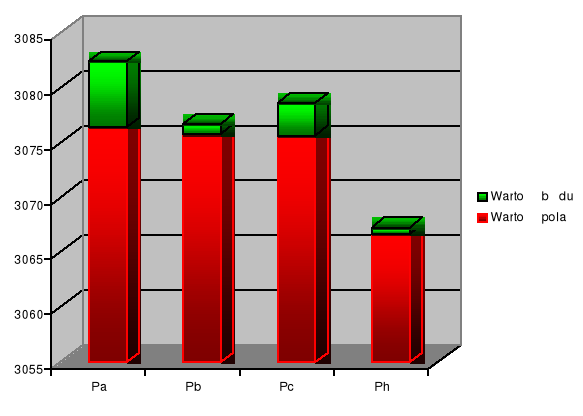
- 1 -

---