WSPÓŁCZYNNIK KORELACJI LINIOWEJ PEARSONA

Współczynnik ten - oznaczany symbolem r
- jest miernikiem siły związku prostoliniowego między dwiema cechami mierzalnymi. Związkiem prostoliniowym nazywamy taką zależność, w której jednakowym przyrostom jednej zmiennej (przyczyny) towarzyszy, średnio biorąc, stały przyrost drugiej zmiennej (skutku).

Współczynnik korelacji liniowej Pearsona jest miarą unormowaną, przyjmującą wartości z przedziału: -1
r

+1. Dodatni znak współczynnika korelacji wskazuje na istnienie współzależności pozytywnej (dodatniej), ujemny natomiast oznacza współzależność negatywną (ujemną). Im moduł (wartość bezwzględna) współczynnika korelacji jest bliższy jedności, tym zależność korelacyjna między badanymi zmiennymi jest silniejsza. Orientacyjnie przyjmuje się, ze korelacja między dwiema cechami jest:

- niewyraźna jeśli r

0,3

- średnia jeśli 0,3 < r

0,5

- wyraźna jeśli r
> 0,5

Interpretacja ta odnosi się również do ujemnych wartości współczynnika korelacji. Jeżeli

r
=
, to zależność korelacyjna przechodzi w zależność funkcyjną. Jeśli natomiast

r
= 0, świadczy to o zupełnym braku związku korelacyjnego między badanymi zmiennymi

X i Y.

Do obliczenia współczynnika korelacji Pearsona stosujemy następujące wzory:

- dla szeregów szczegółowych

r
=

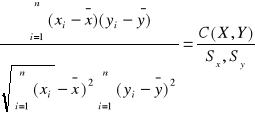
C(X,Y)=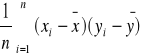
- kowiarancja między cechami X,Y

Sx, Sy -odchylenia standardowe

- dla tablicy korelacyjnej

r
=

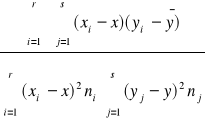
x
, y
- środki przedziałów klasowych

PRZYKŁAD OBLICZANIA KORELACJI LINIOWEJ PEARSONA

Przykład

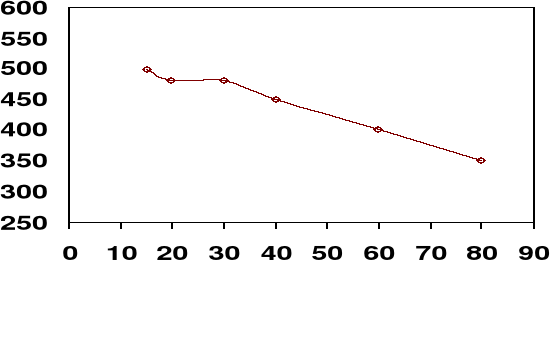
Firma porządkowa przeprowadziła badanie dotyczące ceny świadczonej przez nią usługi oraz liczby osób korzystających z tej usługi. Za pomocą miary korelacji zbadać czy istnieje zależność pomiędzy ceną usługi, a liczbą osób z niej korzystających.

	x	y	x -	y -
1 2 3 4 5 6	15 20 30 40 60 80	500 480 480 450 400 350	-25,8 -20,8 -10,8 -0,8 19,2 39,2	56,7 36,7 36,7 6,7 -43,3 -93,3	-1462,86 -763,36 -396,36 -5,36 -831,36 -3657,36	665,60 432,64 116,60 0,64 368,64 1536,64	3214,89 1346,89 1346,89 28,73 1874,89 8704,89
	245	2660			-7116,66	3120,76	16517,18

Jaka to jest korelacja ?

Jest to korelacja liniowa.

Obliczamy średnią arytmetyczną

=

=

= 40,8

=

=

=443,3

Obliczamy współczynnik korelacji liniowej Pearsona

r
=
=
=
=
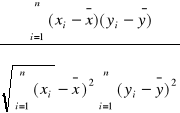
= - 0,99

Współczynnik korelacji r
= - 0,99

Można stwierdzić, że zachodzi silna zależność korelacyjna pomiędzy ceną usługi i liczbą klientów z niej korzystających czyli wraz ze wzrostem ceny usługi maleje liczba klientów korzystających z usług firmy porządkowej.

Korelacja Pearsona

2

---