Ewa Kania 185784

Agnieszka Caputa 185757

Alicja Mostyńska 185771

Patrycja Grzybowska 185817

Grupa XI śr: 15:15-16:45

data wykonania ćwiczenia: 12.10

LABORATORIUM MECHANIKA I WYTRZYMAŁOŚĆ MATERIAŁÓW

Ćwiczenie nr 2

„Doświadczalne wyznaczanie masowego momentu bezwładności”

1. Schemat układu pomiarowego

1. Schemat układu 1

Dane:

m₁=0,232kg

m₂=0,849kg

l=0,283m

d=0,076 => r=0,038m

h=0,062m

gdzie:

m₁-masa pręta

m₂-masa pręta z odważnikiem traktowanym jako walec

l - długość pręta

d - średnica walca

h-wysokości walca

l

h

2. Schemat układu 2

Dane:

m=0,593kg

d₁=0,293m=> r₁=0,1465

d₂=0,334m=>r₂=0,167

s=0,008m

gdzie:

m - masa półpierścienia

d₁ - średnica wewnętrzna pierścienia

d₂ - średnica zewnętrzna pierścienia

s - grubość półpierścienia

2. Obliczanie masowego momentu bezwładności

1. Metoda analityczna

1. Układ 1

• Moment bezwładności pręta

Moment bezwładności pręta wzdłuż osi przechodzącej przez środek ciężkości pręta:

• Moment bezwładności walca

Moment bezwładności względem środka ciężkości walca wyznaczany jest wzdłuż osi przedstawionej na rys.3

• środek ciężkości układu

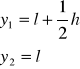
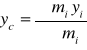
• Moment bezwładności całego układu

Moment bezwładności całego układu wyznaczono z tw. Steinera

gdzie:

a - odległość środka ciężkości układu od osi obrotu

m - masa całego układu

1. Układ 2

• Moment bezwładności półpierścienia względem środka ciężkości:

Moment bezwładności dla pierścienia:

M - masa pierścienia

M=2m, więc dla pierścienia

a dla półpierścienia

• środek ciężkości półpierścienia

Pomijamy grubość półpierścienia i przyjmujemy, że jest on figurą płaską

y

x

Dla półkola środek ciężkości wynosi:

w naszym przypadku:

ze wzoru: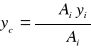
wyznaczamy y_c:

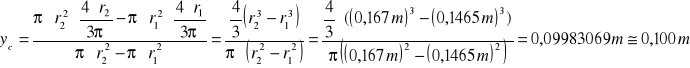
• Moment bezwładności układu:

Moment bezwładności układu wyznaczono z tw. Steinera

Liczymy odległość a środka ciężkości od osi obrotu z tw. Pitagorasa:

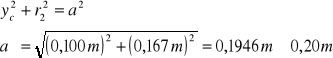
1. Metoda doświadczalna

gdzie:

m-masa bryły

g - przyspieszenie ziemskie

d - odległość osi obrotu od środka masy

T- okres drgań

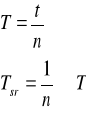
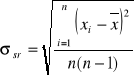
gdzie

n-ilość wszystkich pomiarów

x_i=T_i

=

1. Układ 1

Lp.	n	t [s]	T [s]	Tśr [s]	σśr[s]
1	10	11,0	1,10	1,06	0,05
2			11,0			1,10
3			11,0			1,10
4			11,0			1,10
5			11,0			1,10
6			11,0			1,10
7			10,0			1,00
8			10,0			1,00
9			10,0			1,00
10			10,0			1,00

Tab. 1

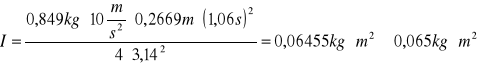
2. Układ 2

Lp.	n	t [s]	T [s]	Tśr [s]	σśr[s]
1	10	9,92	0,992	10,05	0,02
2			9,92			0,992
3			10,07			1,007
4			10,17			1,017
5			9,96			0,996
6			10,45			1,045
7			9,86			0,986
8			10,15			1,015
9			9,92			0,992
10			10,02			1,002

Tab. 2

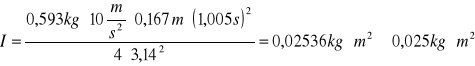
3. Analiza wyników, wnioski:

moment bezwładności [kgxm^2]	pręta z odważnikiem	półpierścienia
metoda analityczna	0,063	0,037
metoda doświadczalna	0,065	0,025

Tab. 3 Tabela wyników

Zestawiając ze sobą otrzymane wyniki, możemy zauważyć, że wyliczone wartości masowego momentu bezwładności brył analitycznie oraz doświadczalnie nieznacznie różnią się od siebie. Różnica dla układu 1 wynosi 0,002kgxm² natomiast dla półpierścienia nieco więcej, bo 0,012. Metoda doświadczalna potwierdza więc prawdziwość twierdzenia Steinera. Te niewielkie różnice mogły wynikać z niedokładności pomiarów czasów za pomocą stopera, np. przez zbyt słaby refleks mierzącego czas. Reasumując obie metody mają podobne skuteczności, a zgodność uzyskanych wyników może świadczyć o poprawności wyniku, przy czym metodę dynamiczną możemy stosować, nie znając dokładnych wymiarów bryły , co może znajdować większe zastosowanie w praktyce.

1

dw

Rys. 1 Schemat układu 1

r₁

r₂

Rys. 2 Schemat układu 2

oś obrotu

Rys. 3

x

y₂

y₁

y

Rys. 4

r₁

r₂

d

Rys. 5

---