Wykład 9 18.04.01.
Struktura pola prędkości płynu
Elementarny ruch dowolnego elementu płynu złożony jest z :
prostego przesunięcia (postępowego),
obrotu elementu,
odkształcenia objętościowego (zmiana długości boków i objętości elementu),
odkształcenia postaciowego elementu (zmiana kątów kształtu elementu).
Odpowiednio odróżnia się :
prędkość ruchu postępowego,
prędkość wirowania,
prędkość odkształcania.
Prędkość odkształceń kątów elementu płynu :
Zmiana kształtu wynika ze zmiany prędkości w kierunku osi x.
Średni kąt obrotu (względem osi z) :
Prędkość kątowa odkształcenia postaciowego elementu to średni kąt obrotu krawędzi odniesiony do jednostki czasu :
W płaszczyźnie Oxy :
W płaszczyźnie Oyz :
W płaszczyźnie Oxz :
Prędkości kątowe odkształcenia objętościowego :
Prędkości kątowe obrotu i odkształcenia po pomnożeniu przez odpowiedni wymiar liniowy elementu wyrażają odpowiednio prędkość wirowania lub prędkość odkształcenia.
Równanie linii wirowej (linii prądu) :
Rotacja wektora prędkości :
Rotacją wektora prędkości v nazywa się następującą zależność :
Zależność pomiędzy składowymi rotacji a składowymi prędkości kątowej chwilowego obrotu xyz jest następująca :
Równanie ciągłości płynu :
Przepływ trójwymiarowy nieustalony płynu nieściśliwego : v=f(x,y,z,t); p=f(x,y,z,t).
Strumień masy - masa przepływająca w jednostce czasu przez daną powierzchnię.
Jednostkowa zmiana strumienia
Jeżeli zapiszemy to jako równanie analityczne : strumień * pole powierzchni * czas = masa
Suma przyrostów masy w objętości elementu w czasie dt :
Przyrost masy wynika ze zmiany gęstości po czasie dt.
Zmiana masy w elemencie płynu wskutek zmiany gęstości :
Pochodne cząstkowe strumieni :
Równanie ciągłości przepływu nieustalonego płynu ściśliwego :
Zmiany gęstości w zależności od położenia
I równanie w czasie
div - dywergencja prędkości = zmiana wektora prędkości (pochodna substancjalna).
Dla ruchu ustalonego płynu ściśliwego ρ 0
Dla ruchu ustalonego płynu nieściśliwego ρ = const.
Sens fizyczny dywergencji wektora prędkości :
Podstawowe równanie opisujące ciągłość przepływu ruchu nieustalonego :
Dywergencja wektora prędkości określa względną zmianę szybkości zmiany objętości płynu :
Dla przepływu ustalonego płynu nieściśliwego dV/dt=0 to divv=0
Natężenie przepływu :
Objętość płynu przepływająca w jednostce czasu lub masa przepływająca w jednostce czasu.
Objętościowe natężenie przepływu :
Jeżeli ρ=ρ(x,y,z,t) to posługujemy się masowym natężeniem przepływu :
Dla płynu nieściśliwego :
Dynamika :
Różniczkowe równanie ruchu Eulera płynu doskonałego :
Płyn doskonały - pozbawiony lepkości.
Siły masowe czynne :
Siły masowe bezwładności :
Zasada d'Alemberta :
Suma rzutów sił na dany kierunek równa jest zero
Analogicznie dla osi y i z
Ogólne równanie ruchu Eulera :
Mechanika Płynów - Wykład 9
- 1 -
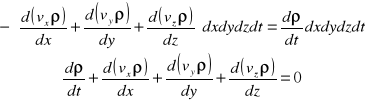
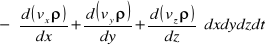
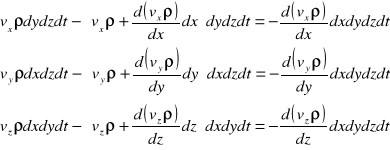
![]()
z
vyρ
dy
vxρ
dz
dx
vzρ
x
y
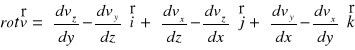
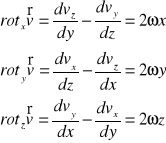
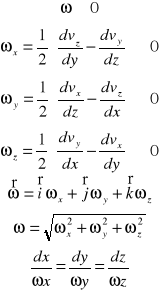
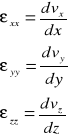
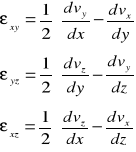
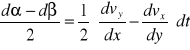
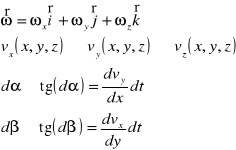
![]()
![]()
y
d
y
d
vy
vx x
x
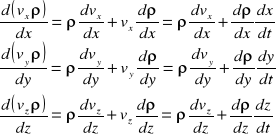
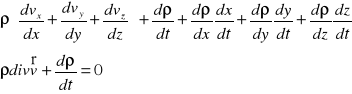
![]()
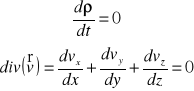
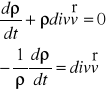
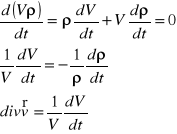
dF
v
F
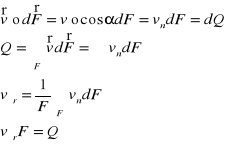
![]()
![]()
(p+dp/dz*dz)dxdy
z
pdxdz
pdydz z (p+dp/dx*dx)dydz
x
z
(p+dp/dy*dy)dxdz pdxdy
x
y
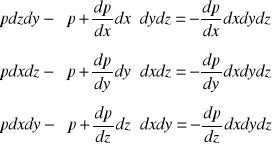
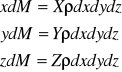
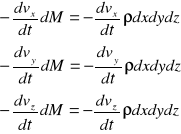
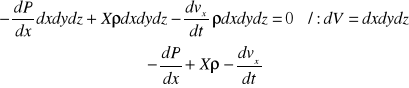
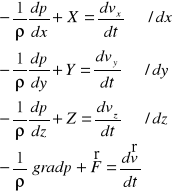
Wyszukiwarka
Podobne podstrony:
Koral 13, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 14, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 11, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 19, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 15, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 12, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 10, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Koral 16, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Newton jest jak Herkules z bajki, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
PLYNY4~1, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Podstawowe charakterystyki temperatury powietrza, Księgozbiór, Studia, Mechanika Płynów i Dynamika G
ruch laminarny2, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
POLITE~2, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
więcej podobnych podstron