Wydział EAIiE	Imię i nazwisko : Krzysztof Lisowski Przemysław Mrawczyński		Rok pierwszy		Grupa 4		Zespół 2
Pracownia fizyczna I	Temat: Wyznaczanie modułu Younga.						Nr ćwiczenia 11
Data wykonania:	Data oddania	Zwrot do popr.		Data oddania		Data zaliczenia	Ocena

Cel ćwiczenia:

Celem ćwiczenia jest wyznaczenie modułu Younga metodą statyczną mierząc wydłużenie drutu wykonanego z danego materiału obciążonego stałą siłą.

Wstęp teoretyczny:

Jeśli na jakieś ciało wywrzemy pewną siłę to może ono ulec odkształceniu - deformacji. Może ono mieć postać związaną ze zmianą objętości - odkształcenie objętościowe lub też ze zmianą kształtu ciała - odkształcenie postaci. Siła odkształcająca prowadzi do przemieszczania cząsteczek z początkowych położeń równowagi w węzłach sieci krystalicznej do nowych. Przeciwdziałają temu siły międzycząsteczkowe, które w tym przypadku są siłami sprężystości. Są one równe co do wartości, ale przeciwnie skierowane do sił odkształcających. Siła międzycząsteczkowa rośnie liniowo wraz z odkształceniem. Opisuje to prawo Hooke'a:

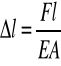
gdzie:

• Δl - przyrost długości pręta

• l - długość pręta

• F - siła rozciągająca

• A - pole powierzchni przekroju pręta

• E - stała materiałowa (moduł Younga)

Moduł Younga - zależy od rodzaju odkształcenia materiału, temperatury oraz od obróbki termicznej i mechanicznej materiału i jest równy takiemu naprężeniu normalnemu, przy którym liniowy wymiar ciała ulega podwojeniu. Na jego podstawie możemy się zorientować o wielkości sił wewnętrznych (sprężystych) w danym materiale.

W momencie ustania działania zewnętrznej siły odkształcającej siły napięć wewnętrznych spowodują powrót do swych pierwotnych wydłużeń. Nastąpi to jednak wtedy gdy siła odkształcająca nie przekroczy pewnej granicy sprężystości. W przeciwnym bowiem razie doznane odkształcenia ciała nie ustąpią z chwilą zniknięcia sił zewnętrznych. Takie odkształcenie nazywamy plastycznym.

Prawo Hooke'a jest słuszne jedynie w odniesieniu do odkształceń sprężystych a więc znikających z działaniem sił zewnętrznych.

W naszym doświadczeniu nie przekraczamy progu sprężystości więc do wyznaczenia modułu Younga będziemy stosować prawo Hooke'a.

Po przekształceniu wzoru opisującego prawo Hooke'a i uwzględnieniu zależności p = F/S otrzymujemy:

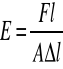
Mając daną rozciągającą siłę zewnętrzną, powierzchnię przekroju i długość ciała, oraz mierząc wydłużenie Δl jesteśmy w stanie wyznaczyć moduł Younga dla danego materiału.

Aparatura:

Do wykonania ćwiczenia potrzebne są następujące pomoce:

• statyw do pomiaru modułu Younga,

• przymiar liniowy,

• śruba mikrometryczna,

• ciężarki,

Przebieg ćwiczenia i opracowanie wyników:

1. Ustawić pionowo statyw przyrządu, regulując głębokość zakręcenia nóżek podstawy i obserwując wskazania pionu.

2. Przymiarem liniowym zmierzyć długość drutów stalowego (L_s) i miedzianego (L_m) z dokładnością 1 mm. Za pomocą śruby mikrometrycznej zmierzyć średnicę drutów (d_s - stalowego, d_m - miedzianego ). Pomiar średnicy należy wykonać 10 razy wzdłuż całej długości drutów i obliczyć wartość średnią.

3. Wyznaczyć zależność wydłużenia drutu stalowego (Δl_s) od wartości siły rozciągającej. Masę obciążającą zmieniać co 1 kg w granicach od 0 do 10 kg. Pomiar wykonać dla rosnących a następnie dla malejących wartości ciężaru.

4. Wykonać analogiczny pomiar dla drutu miedzianego.

5. Sporządzić wykres Δl = f(F) dla obu drutów.

6. Dla drutu stalowego metodą najmniejszych kwadratów znaleźć wartość i błąd współczynnika nachylenia - prostoliniowej części wykresu.

7. Obliczony współczynnik nachylenia prostej regresji a = Δl/ΔF wykorzystać do obliczenia modułu Younga stali.

8. Obliczyć błąd ΔE.

9. Obliczyć moduł Younga miedzi określając a metodą graficzną.

10. Porównać znalezione wartości z wartościami tablicowymi.

1. Wykonujemy pomiary dla drutu stalowego

Długość drutu stalowego

L_s = 1,066 ± 0,001 m

Średnica drutu stalowego

Lp.	d [mm]
1	0,71
2	0,71
3	0,72
4	0,71
5	0,71
6	0,71
7	0,72
8	0,72
9	0,71
10	0,71
Średnia	0,713

Wartość średnia ± odchylenie standardowe :

d_s = 0,713 ± 0,005 mm

Tabele przedstawiają wyniki pomiarów dla drutu stalowego :

Lp.	m [kg]	Δ l [mm]	F [N]
1	0	0,00	0,0
2	1	0,33	9,8
3	2	0,66	19,6
4	3	0,95	29,4
5	4	1,24	39,2
6	5	1,52	49,0
7	6	1,81	58,8
8	7	2,12	68,6
9	8	2,49	78,4
10	9	2,72	88,2
11	10	2,96	98,1

Lp.	m [kg]	Δ l [mm]	F [N]
1	10	3,00	98,1
2	9	2,72	88,2
3	8	2,47	78,4
4	7	2,10	68,6
5	6	1,82	58,8
6	5	1,51	49,0
7	4	1,22	39,2
8	3	0,94	29,4
9	2	0,66	19,6
10	1	0,32	9,8
11	0	0,02	0,0

- Metodą najmniejszych kwadratów znajdujemy wartość i błąd współczynnika nachylenia prostej regresji a :

Regresja liniowa to wyrównanie do prostej postaci :

y = ax + b

W naszym przypadku :

y - wartość bezwzględnego wydłużenia Δl;

x - masa m;

n - liczba punktów pomiarowych;

m - ilość obliczanych parametrów (a,b)

(2)

(3)

Obliczamy błąd Δa

(4)

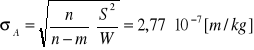
i błąd Δb

(5)

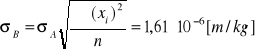
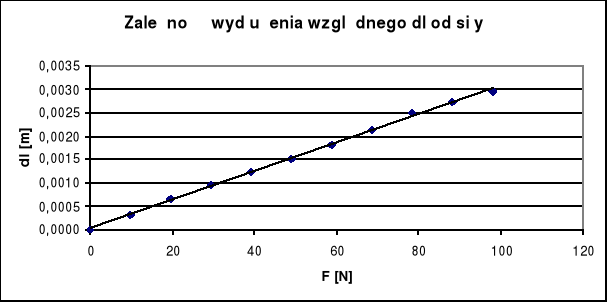
Tworzymy wykres zależności wydłużenia dl od siły F

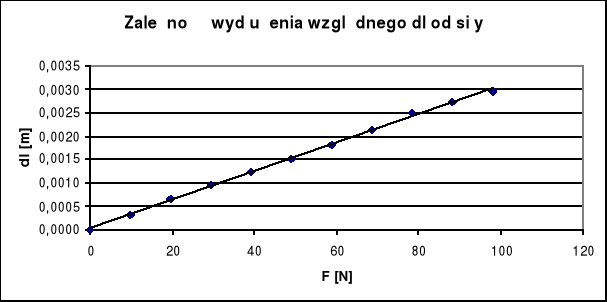
Obliczamy pole przekroju drutu:

A=4 ⋅10^-7 [m²]

Obliczamy błąd ΔA

Obliczamy moduł Younga

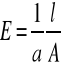
E = 0,89 *10 ¹¹ [Pa]

Z prawa przenoszenia błędów obliczamy błąd ΔE :

ΔE = 8,22 ⋅10⁸ [Pa]

Zestawienie

E	0,89 *10 ^11 [Pa]
ΔE	8,22*10^8 [Pa]
Etabl	2*10^11 [Pa]
ΔE/E *100%	1%

Niestety jak widać uzyskany przez nas wynik jest ponad 2 razy mniejszy od wartości tablicowej. Wynikać może to z niedokładności wykonania pomiarów, niedokładności przyrządów, czy też ze zwykłego, ludzkiego błędu .

2. Wykonujemy analogiczne pomiary dla drutu miedzianego

Długość drutu miedzianego

L_m = 1,072 m

Średnica drutu miedzianego

Lp.	d [mm]
1	1,012
2	1,011
3	1,011
4	1,012
5	1,011
6	1,011
7	1,011
8	1,012
9	1,011
10	1,011
Średnia	1,0113

d_m = 1,0113 ± 4,83 ⋅10^-4 [mm]

Tabele przedstawiają wyniki naszego doświadczenia :

Lp.	m [kg]	Δ l [mm]	F [N]
1	0,5	0,12	4,9
2	1	0,30	9,8
3	1,5	0,47	14,7
4	2	0,61	19,6
5	2,5	0,75	24,5
6	3	0,88	29,4
7	3,5	1,02	34,3
8	4	1,16	39,2
9	4,5	1,30	44,1
10	5	1,43	49,0
11	5,5	1,55	53,9
12	6	1,69	58,8

Lp.	m [kg]	Δl [mm]	F [N]
1	0,5	0,20	4,9
2	1	0,39	9,8
3	1,5	0,55	14,7
4	2	0,71	19,6
5	2,5	0,83	24,5
6	3	0,98	29,4
7	3,5	1,10	34,3
8	4	1,25	39,2
9	4,5	1,37	44,1
10	5	1,50	49,0
11	5,5	1,63	53,9
12	6	1,76	58,8

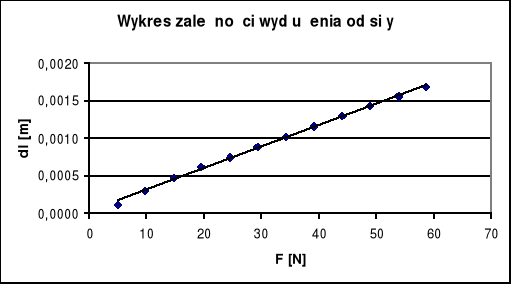
Tworzymy wykres zależności wydłużenia od siły

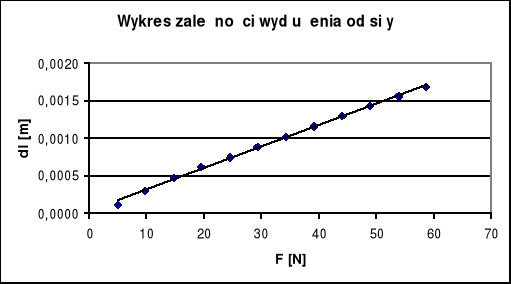
Metodą najmniejszych kwadratów wyznaczamy współczynnik nachylenia prostej regresji i wyznaczamy błąd

a = 3 ⋅10^-5

b = 3 ⋅10^-5

σ_a = 9,4 ⋅10^-7

σ_b = 3,4 ⋅10^-6

Obliczamy pole powierzchni przekroju drutu miedzianego

A = 8 ⋅10^-7 [m²]

ΔA = 1,6 ⋅10^-8 [m²]

Wyliczamy moduł Younga E uwzględniając błąd i porównujemy z wynikiem tablicowym

E = 4,5 ⋅10¹⁰ [Pa]

ΔE = 1,6 ⋅10⁹ [Pa]

E	4,5 ⋅10^10[Pa]
Δ E	1,6 ⋅10^9[Pa]
Etabl	1,3 ⋅10^11 [Pa]
ΔE	3,7 [%]

I tym razem wynik naszego doświadczenia znacznie różni się od wartości tablicowej. Niestety, przy tak dokładnych pomiarach błąd ludzki jest znaczący.

8

---