Równanie różniczkowe o zmiennych rozdzielonych

Równaniem różniczkowym o zmiennych rozdzielonych nazywamy równanie postaci

gdzie funkcje f i g są określone i ciągłe odpowiednio w przedziałach
oraz

Sposób rozwiązywania takiego równania wyjaśnimy na przykładach.

Przykład 1. Rozwiązać równanie dla x i y różnych od 0:

Rozdzielamy zmienne:

i całkujemy lewą stronę względem y, zaś prawą stronę względem x:

Odpowiednie całki obliczamy na kalkulatorze ClassPad 300:

tak więc mamy

,

albo lepiej zapisać, że

gdzie C oraz K oznaczają pewne stałe.

Sprawdźmy, za pomocą ClassPada rozwiązanie wygląda tak:

Przykład 2. Rozwiązać równanie:

Mamy kolejno:

o ile

Rozdzieliliśmy zmienne, a więc

czyli

a więc rozwiązanie równania, tzw. całka ogólna (CORR), jest podana w postaci uwikłanej. Wstawiając do danego równania
stwierdzamy, że jest to również rozwiązanie, podobnie jak i
Są to tzw. całki szczególne równania różniczkowego (CSRR), których nie można otrzymać z całki ogólnej.

Ostatecznie piszemy:

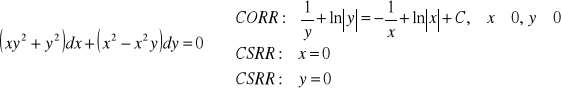
Przykład 3. Znaleźć całkę równania:

przy warunku początkowym

Znajdujemy najpierw CORR:

czyli
Skoro
więc
zatem
Całką danego równania, zwaną również całką szczególną, jest
czyli

Sprawdźmy, za pomocą ClassPada rozwiązanie wygląda tak:

---