1.3 Statystyka jako badanie populacji
Statystyka jest działem metodologii naukowej. Jej celem jest opis i wyciągnięcie wniosków dotyczących właściwości ilościowych populacji.
Termin POPULACJA - jest używany w odniesieniu do grup lub zespołów ludzkich, ale według statystyków nie odnosi się ten termin tylko do ludzi , ale do wszelkich zbiorów np. zwierzat, zdarzeń czy rzeczy lub także zbiorów pomiarów np. biurka. Statytstyke interesują właściwości grupy , nie pojedynczych elementów.
1.4 Statystyka jako badanie zmienności
Statystyka dysponuje róznymi technikami umożliwiającymi poszukiwanie zmienności wśród zdarzeń naturalnych oraz wyciąganie wniosków o przyczynach tej zmienności.
Pearson - uczeń Galtona, stworzył matematyczne podstawy statystyki. Fisher rozwinął analize wariancji i przyczynil się do rozwoju wielu innych dziedzin statystyki
1.5 Próby i ich pobieranie
Jeżeli populacja jest zbyt duża to sporządzenie statystyk na jej podstawie jest rzecza niemozliwą. W takim momencie badacz pobiera tzw. Próbę. Próbą jest dowolna podgrupa lub też podzespół wybrany z populacji przy uzyciu odpowiedniej metody np:
prosta próba losowa (czyli po prostu losowe wybranie elementów z populacji),
próba kwotowa ( najpierw grupa dzielona jest na podgrupy, a następnie ankieter lub eksperymentator wybiera z każdej podgrupy przypadki w odpowiedniej proporcji),
próba warstwowa ( tak jak w przypadku kwotowej wymaga podzielenia operatu na podgrupy, jednak z każdej grupy obiekty do próby wybierane są losowo.),
próba grupowa (operat jest dzielony na grupy, a następnie losowane są do próby nie pojedyncze jednostki, lecz całe grupy.),
losowanie dwustopniowe (Podobnie jak w próbie grupowej losowane są najpierw grupy, jednak nie wchodzą one w całości do próby, lecz przeprowadzane jest z nich kolejne losowanie.),
próba losowo-kwotowa (Losowanie dwustopniowe, w którym najpierw losuje się miejscowości (wiejskie i miejskie), a następnie wykonuje próbę kwotową. Ma wszystkie wady próby zespołowej i próby kwotowej, choć efekt jest nieco lepszy dzięki zapewnieniu właściwych proporcji miast i wsi.),
próba systematyczna (Wybór badanych w jakikolwiek systematyczny sposób np. co 10 nazwiska z książki telefonicznej. Jeśli zmienna według której wybieramy (czyli tu: pozycja w książce telefonicznej) jest niezależna od wszystkich zmiennych badanych, to próba jest reprezentatywna-część populacji, wybrana do badania metodami statytstycznymi, w założeniu badacza, zachowująca strukturę wyróżnionych cech populacji przy założonym poziomie istotności.),
próba ekspercka/ dobór celowy (W tym schemacie losowania grupy badanych są dobierani do próby przez ekspertów, np. aby przewidzieć wynik wyborów, bierze się pod uwagę miejscowości, gdzie wyniki w poprzednich wyborach były najbardziej zbliżone do wyników w skali kraju.)
Po pobraniu proby badacze opisują jej właściwości. Póżniej przystępują do formulowania twierdzeń na podstawie wyciągniętych wniosków.
Statystyka opisowa
Procedury stosowane do opisu właściwości próby lub populacji niektórzy autorzy określaja mianem statystyki opisowej(dział statystki zajmujący się metodami opisu danych statystycznych uzyskanych podczas badania statystycznego. Celem stosowania metod statystyki opisowej jest podsumowanie zbioru danych i wyciągnięcie pewnych podstawowych wniosków i uogólnień na temat zbioru.).
Staytystyka indukcyjna
Procedury statystyczne stosowane przy wyciąganiu wniosków dotyczących właściwości populacji na podstawie danych uzyskanych z próby często określa się mianem statystyki indukcyjnej (1.zajmuje sie wnioskowaniem o cechach populacji w oparciu o cechy wylosowanej z niej próby (proces ten nosi nazwe estymacji).weryfikacja hipotezy statystycznej odbywa się przez zastosowanie specjalnego narzędzia - test istotności. (definiuje problem, zbiorowość=>wyznacza populację. 2.pozwala ustalić prawidłowości i podejmować decyzje na podstawie zredukowanej liczby dowolnych przy zastosowaniu rachunku prawdopodobieństwa. Dzieki niemu możliwe jest określenie jaki błąd popełniamy, uogólniając wyniki z próby na całą zbiorowość.)
1.6 Parametry i estymatory
Parametr
To właściwość opisujaca populację. Zazwyczaj parametry albo właściwości populacji pozostaja nieznane. Dokonujemy ich oszacowania na podstawie wartości uzyskanych w próbach. Parametr oznacza się literami greckimi- grecka litera sigma Σ - stosowane do sumowania lub σ - do odchylenia standardowego w populacji czyli powszechnie stosowanego miernika zmienności. parametry rozkładu badanej cechy w populacji, charakteryzują one ten rozkład. Do najczęściej używanych parametrów należą tzw. MOMENTY
Estymator
Właściwośc próby pobranej losowo z populacji. Oznacza się go literami łacińskimi - na oznaczenia estymatora parametru σ stosowany jest symbol s. Estymator to dowolna statystyka Z służąca do oszacowania nieznanej wartości parametru. Celem zastosowania estymatora jest znalezienie parametru rozkładu cechy w populacji.
Błąd próby - rożnica miedzy parametrem, a estymatorem. Jak oszacować wielkość błędu estymatora gdy parametr jest nieznany? Np. wielokrotnie powtarzając pomiar
1.7 Zmienne i ich klasyfikacja
Terminem zmiennej określa się właściwość, pod której względem elementy grupy różnia się miedzy sobą. Np. jeśli bierzemy pod uwage grupe gdzie elementami są ludzie - mogą się oni różnić miedzy soba miedzy innymi wiekiem, płcią , kolorem oczu itp. Terminem stała okresla się właściwości pod względem których elementy nie różnią się miedzy sobą. Istenija zmienne dwuwartościowe - czyli np. płeć, człowiek może być kobieta lub mężczyzną, albo wielowartościowe zmienne np. taka właściwością jest zawód.
Można wyróżnić zmienne zależne i niezależne:
- zmienna zależna jest to cecha, która interesuje nas w konkretnym badaniu, której związki z innymi chcemy poznać. Np. wyrażenie Y= f(X) : Zmienna Y jest zalezna od zmiennej (X) i od zalezności funkcyjnej f.
- Zmienna niezależna to cecha od której zależy zmienna zależna która oddziałuje na tą zmienną. Np. kiedy badamy poziom wykształcenia dzieci określonego miasta, to poziom ich wykształcenia stanowi zmienną zależną. Zmienne niezależne to np. poziom wykształcenia rodziców, praca warunki życia itd. wszystko to co może oddziaływać na wykształcenie dzieci. Np. wyrażenie Y= X³ , widzimy, ze można latwo na podstawie zmienne Y obliczyc zmienną X, która nie jest od niej zalezna.
Jest także rozróżnienie między zmiennymi ciągłymi i dyskretnymi ( nieciągłymi).
- Ciągła może przymować dowolna wartość z określonego zakresu wartości. Przykładami zmiennych ciagłych mogą być np. wzrost, waga i czas.
- Zmienna nieciągła ( dyskretna) może przyjmowac tylko niektóre wartości np. w rodzinie może być 1, 2, 3 dzieci, ale nie mogą występować wartości pomiedzy tymi liczbami.
Istenieje także klasyfikacja opierajaca się na roznicach miedzy typami informacji, jakie dostarczaja różne operacja klasyfikowania i pomiaru. Można tutaj wyodrębnić 4 rodzaje zmiennych:
- nominalna
Jest właściwością elementów należących do takiej grupy, która została wyznaczona przez operację pozwalającą na formułowanie twierdzeń o równości lub różności. W przypadku zmiennej nominalnej możemy twierdzić, że jeden element jest pod względem interesującej nas właściwości taki sam albo inny niż drugi element. Nie możemy natomiast formułować twierdzeń o uporządkowaniu elementów, o jednakowości różnic między elementami ani o tym, ile razy jeden element jest większy lub mniejszy niż drugi.
- porządkowa
Jest właściwością określoną przez operację, która pozwala na uszeregowanie elementów grupie. Możliwe są tutaj nie tylko twierdzenia o równości bądź różności elementów, lecz także twierdzenia typu "..większy niż" i "mniejszy niż". Twierdzenia o jednakowości różnic między elementami, albo o tym ile razy jeden element jest większy lub mniejszy niż drugi, nie są możliwe.
- przedziałowa
Jest właściwością określoną przez operację, która pozwala na formułowanie, obok twierdzeń o równości lub różności i twierdzeń typu ,"większy niż" i "mniejszy niż", również do twierdzeń o równości przedziałów. Zmienna przedziałowa nie ma ,,oryginalnego" punktu zerowego, aczkolwiek taki punkt zerowy można sobie dowolnie wyznaczyć.
- stosunkowa
Jest właściwością określoną przez operację, która pozwala na formułowanie, obok wszystkich typów twierdzeń omówionych poprzednio, również do twierdzeń o równości stosunków.
Znaczy to, że można mówić, iż jedna wartość zmiennej jest dwa lub trzy razy taka jak druga. W przypadku zmiennej stosunkowej zawsze istnieje zero absolutne. Użyte liczby odzwierciedlają odległość od naturalnego początku.
Zasadnicza różnica między zmienna stosunkową, a przedziałowa polega na tym, że w przypadku zmiennej stosunkowej pomiarów dokonuje się poczynając od prawdziwego punktu zerowego! Zaś w przypadku zmiennej przedziałowej od punktu zerowego lub od początku określonego arbitralnie ( czyli jakby narzuconego).
badanie korelacyjne - schemat badawczy, który służy do oceny siły związku między zmiennymi; nie pozwala na wyciąganie wniosków dotyczących przyczyn.
Eksperyment - w badaniach jedna lub wiele zmiennych może być stworzonych przez badacza, który okresla jakie wartości przyjmuje zmienna i jaka liczba jest tych zmiennych.
1.8 Analiza danych
Wstepna analiza danych ma charakter opisowy, obejmuje proste operacje. Ma ona na celu zrozumienie przez badacza charakteru i struktury danych, a w konsekwencji dobranie odpowiednich modelów statystycznych.
ROZDZIAŁ 2
2.1 Wprowadzenie
Do opisu liczb ( danych z badań) potrzebne są pewne formy klasyfikacji i opisu. W pewnych okolicznościach przydatna jest klasyfikacja danych majaca forme rozkładu liczebności. Rozdzial ten jest poświęcony rozkładowi liczebności, graficznemu przedstawieniu tych rozkładów oraz temu jak mogą one się roznic miedzy soba.
Rozkładem liczebności jest kazde uporządkowanie danych, które pokazuje liczebność różnych wartości zmiennej lub liczebność wartości należących do dowolnie określonych grup zmiennej, zwanych przedziałami klasowymi.
2.2 Rozkłady liczebności
Po rzucaniu moneta 10 razy otrzymujemy wyniki O O R O O R O O O R. Dane te można ułożyć w następującej tabelce:
X |
f |
O R |
7 3 |
Razem |
Σ = 10 |
Symbol f - ilość . Takie uporządkowanie danych nosi nazwę ROZKŁADU LICZEBNOŚCI. Uporzadkowanie pokazujące jak często pojawiają się orły i reszki.
Gdy liczba grup wyników jest duża zaleca się okgraniczenie liczby klas przez uporządkowanie danych w dowolnie określone grupy zmiennej. Np. jeśli badamy iloraz inteligencji 100 uczniów i wyniki obejmuja wartości od np. 67 do 134 , możemy wszystkie wyniki mieszczące się miedzy 65, a 69 czyli 65, 66,67,68 i 69, można zgrupować razem I tak dalej. Dowolnie określone grupy zmiennych noszą nazwę przedziałów klasowych. Czyli tabelka wyglądałaby mniej więcej tak:
Przedział klasowy - czyli co 5 liczb |
Liczebnośc f |
130- 134 125-129 …. 70-74 65-69 |
15 1 w pozostałych przedziałach było 77 osób 15 2 |
Razem |
100 - ponieważ było badanych 100 ucznów |
Przedzial klasowy równy w tym przypadku jest 5.
2.3 Zasady posługiwania się przedziałami klasowymi.
Jeśli przedział klasowy jest równy 1, wyniki można odtworzyc bez żadnej straty informacji. Jeśli przedział klasowy jest wiekszy ( 3,5 lub 10) narazamy się na pewna stratę informacji - na podstawie rozkładu liczebności nie możemy wtedy dokadnie odtworzyc wyników oryginalnych.
2.4 Granice dokładne przedziałów klasowych
Jeśli mamy przedział klasowy : 130 - 134 to jego granicami będzie 129,5 - 134,5 , a jego środkiem 132.
Rozkład wyników w obrębie przedziału klasowego.
Przy obliczeniu pewnych statystyk i przygotowaniu przedstawienia graficznego należy dokonac pewnych założeń dotyczących wartości w obrębie przedziałów. Możemy sformułowac dwa takie zalożenia:
Wyniki rozkładają się równomiernie w dokładnych granicach przedziału. Założenie to przyjmuje się przy obliczaniu takich statystyk jak mediana, kwartyle, centyle i przy rysowaniu histogramów.
Zgodnie z drugim zalożeniem wszystkie wyniki skupiaja się w środku przedziału czyli wszystkie wyniki z tego przedziału są identyczne, a zarazem równe wartości odpowiadającej środkowi przedziału. ( Środek dowolnego przedziału klasowego leży w połowie między dokładnymi granicami tego przedziału np. jeśli mamy przedział 99,5 - 104,5 to jego środkiem będzie 102) Zalożenie to przyjmuje się przy obliczaniu takich statystyk jak odchylenie standardowe, średnia oraz przy rysowaniu krzywych liczebności.
Rozkład liczebności skumulowanych.
Jesli interesuje nas procentowy udział wartości „większych niż” bądź „mniejszych niż” pewna określona wartość to sporządzamy rozkład liczebności skumulowanych. Liczebności skumulowane otrzymujemy dodając kolejno - zaczynając od dołu liczebności jednostkowe. Skumulowany procent liczeności otrzymuje się poprzez podzielenie liczebności skumulowanej przez całkowita liczbę przypadków - czyli przez RAZEM = ileś * Rozkład liczebności skumulowanych pozwala nam stwierdzić w jakiej liczbie przypadków wyniki są niższe od pewnej określonej wartości.
2.7 Tabele
2.8 Wykresy
2.9 Histogramy
Jest to wykres w którym liczebności przedstawione są w postaci słupków.
2.10 Wieloboki liczebności
Wszystkie przypadki w każdym przedziale skupiają się w jego środku ( a w histogramie równomiernie) Kropki stawiamy w połowie przedziału kolo liczebności
2.11 Wieloboki liczebności skumulowanych
Rózni się tym od wieloboku liczebności , że zamiast stawiania kropek odpowiadających liczebnością surowym, stawiamy kropki liczebnością skumulowanym i robimy to na granicy przedziału, a nie w środku.
Apropo sporządzania wykresów , gdyby Pani A prosiła to : na osi poziomej X przedstawia się wyniki, a na Y liczebności.
Y
X
2.13. Różnice między rozkładami liczebności
Rozkłady liczebności charakteryzuje się za pomocą 4 cech, są to:
-tendencja centralna : określa ja wartośc znajdujaca się w pobliżu środka rozkładu liczebności. Jest to watośc centralna.
-zmienność okresla stopień w jakim wartości rozproszone są wokół wartości centralnej.
-skośność określa symetrycznośc bądź niesymetryczność rozkładu liczebności ( jeśli jest niesymetryczny i istnieje tendencja do skupiania się wiekszych liczebności w zakresie mniejszych wartości zmiennej to mówimy ze jest to rozklad skośny dodatni, jeśli jest odwrotnie to skośny ujemny).
-kurtoza(spiczastość) okresla płaskośc lub stromość jednego rozkładu w stosunku do innego. Jeśli jeden rozkład jest bardziej stromy niż drugi to jest on bardziej leptokurtyczny, a jeśli mniej to platykurtycznya, a rozkład normalny - mezokurtycznym.
ROZDZIAŁ 3- ZAPIS STATYSTYCZNY
3.1 Wprowadzenie
Najczęściej stosowaną postacia zapisu statystycznego jest zapis sumowania. Zapis ten opiera się na kilku bardzo prostych zasadach.
3.2 Przedstawienie zmiennych w postaci symboli
Dowolna wartość zmiennej przyjęło się określać symbolem Xi gdzie indeks i = może przyjmowac dowolną wartość od 1 do N, jako indeksów uzywa się również symboli j oraz k.
3.3 Sumowanie wartości zmiennej.
Jest to zsumowanie elementów
Σ = X1 + X2 + … + Xn
3.4. Reguła posługiwania się zapisem sumowania.
3.5. Zapis stosowany w rozkładach liczebności.
ROZDZIAŁ 4 - MIARY TENDENCJI CENTRALNEJ
4.1 Wprowadzenie
Termin tendencja centralna określa pewną wartość stanowiącą centralny punkt odniesienia. Wartość ta jest zazwyczaj bliska punktowi największego skupienia pomiarów i w pewnym sensie można ja uważać za typową dla całego zbioru. Powszechnie stosowanymi miarami tendencji centralnej są :
- wartość modalna (moda) (Moda i mediana stosowane są dla zmiennych nominalnych i porządkowych)
- mediana
- średnia arytmetyczna - najczęściej stosowana ( dla zmiennych przedziałowych i stosunkowych)
- średnia harmoniczna
- średnia geometryczna ( te dwie ostatnie są raczej rzadko stosowane)
4.2 Średnia arytmetyczna.
Suma zbioru pomiarów podzielona przez liczbę pomiarów w zbiorze.
4.3 Obliczanie średniej z rozkładów liczebności
Mamy podane wartości X , dodajemy je i dzielimy przez liczbę pomiarów ( ilość X)
4.4. Odchylenie od średniej
Jest to różnica miedzy pewnym konkretnym wynikiem X, a średnią. Czyli aby obliczyc odchylenie od sredniej
należy odjąć od wartości X średnia arytmetyczną. Wyniki te są tzw. Odchyleniami, ich poprzednia postać była wynikami surowymi.
4.5 Niektóre cechy sredniej arytmetycznej
Suma odchyleń wszystkich pomiarów w zbiorze od ich średniej arytmetycznej jest równa zero. [
Suma kwadratów odchylen od średniej arytmetycznej jest mniejsza niż suma kwadratów odchyleń od dowolnej innej wartości. - ta cecha średniej wskazuje, że stanowi ona centrum, środek ciężkości zbioru pomiarów.
4.6 Mediana
Mediana jest tendencja dzieląca wszystkie pomiary na pół. Jest to środkowa liczba , gdy w danym zbiorze jest nieparzysta ilość liczb. Jednak kiedy mamy parzystą ilośc liczb dodajemy dwie środkowe i dzielimy na dwa.
4.7 Obliczanie mediany dla rozkładów liczebności
Najpierw zapisujemy liczebności skumulowane.
Później okreslamy wartość N/2 czyli połwę przypadków ( Suma dzielona przez 2)
Później odszukujemy przedział klasowy w którym mieści się nasze N/2 ( patrzymy na wartości skumulowane i w nich szukamy!)
Patrzymy ile przypadków znajduje się nie w liczebności skumulowanej , w tym przedziale
me = xdi+ (n/2-fci-1/fi)*hi
xdi Dokładna DOLNA granica przedziału, w którym jest mediana
fci-1 Liczebność skumulowana klasy WCZEŚNIEJSZEJ niż mediana
fi Liczebność klasy medialnej
hi Długość przedziału klasowego
4.8 Cechy mediany
4.9 Wartość modalna
W sytuacjach w których różne wartości zmiennej X wystepuja więcej niż raz wartośc modalna jest wartością występującą najczęściej. Czyli jeśli mamy przykład:
1 1 1 3 3 3 3 5 5 9 to wartościa modalną w tym przypadku jest 3, ponieważ stepuje najwięcej razy. Jeśli wszystkie cyfry występują w tej samej ilości to NIE DA się obliczyć mody. Jeśli np. dwie z cyfr występują tyle samo razy, ale wiecej niż pozostałe to wyliczamy z nich średnia arytmetyczną.
4.10 Porównanie średniej, mediany i wartości modalnej.
Srednia arytmetyczna -> zmienne przedziałowe i stosunkowe
Mediana -> Zmienne porządkowe.
Wartośc modalna -> jest statystyka nominalną
Mediana dzieli przedział na dwie rowne części. Srednia jest centrum lub środkiem ciężkości rozkładu. Wartość modalna jest punktem odpowiadającym najwyższemu punktowi krzywej.
4.11 Inne miary tendencji centralnej
Średnia geometryczna ŚG =
Mnożymy wszystkie wartości i wyciagamy z nich pierwiastek ( taki ile jest cyfr )
ROZDZIAŁ 5 - MIARY ZMIENNOŚCI, SKOŚNOŚCI I KURTOZY
5.1 Wprowadzenie
Wśród miar stosowanych do opisu zmienności wyróżniamy rozstęp, odchylenie przeciętne i odchylenie standardowe. Najważniejszym z nich jest odchylenie standardowe.
5.2 Rozstęp
Jest to różnica miedzy największym i najmniejszym pomiarem.
5.3 Odchylenie przeciętne
Sumujemy wszystkie odchylenia od średniej i dzielimy to przez N.
5.4 Wariancja i odchylenie standardowe
Wariancja w populacji:
σ2 = Σ ( X - µ)2 / Np - otrzymujemy średni kwadrat odchylenia
σ2- wariancja w populacji - średnia arytmetyczna
µ - średnia w populacji - ( X - µ)2 - kwadrat odchylenia od średniej
Np. - liczba elementów populacji
Wariancja z próby ( stosowana jako estymator σ2)
Czyli Suma ( x- x śr ) 2 podzielona przez liczbę pomiarów w próbie minus 1.
Na czym polega istota różnicy między zastosowanie N czy N - 1 ?
Wartość otrzymana przez podzielenie sumy kwadratów przez N daje obciążony estymator σ2
Odchylenie standardowe. Czyli wyciagnięcie pierwiastka kwadratowego z wariancji.
W populacji :
Z próby:
Im większa wartość odchylenia standardowego tym bardziej obserwowane wielkości oddalone są od średniej. Im mniejsza wartość, tym bardziej są skupione wokół średniej.
5.5 Przykład zastosowania wariancji i odchylenia standardowego
5.6 Obliczenia wariancji z próby i odchylenia standardowego z danych nie pogrupowanych
5.7 Wpływ dodawania wartości stałej lub mnożenia przez wartość stałą na odchylenie standardowe.
Jeśli do wszystkich pomiarów z próby dodamy pewna wartość stałą to odchylenie standardowe pozostanie nie zmienne. Np. Pani A. dochodzi do wniosku na egzaminie ze statystyki, że egzamin jest zbyt trudny i do każdej oceny dodaje 10 ptk ( marzenie!) W efekcie odchylenie standardowe ocen jest takie samo po dodaniu 10 ptk jak przed dodaniem.
5.8 Wyniki standardowe
Wyniki pierwotne z badania to wyniki surowe : wynik oznacza się symbolem X, średnia X z kreską, a odchylenie s . Odchylenia od sredniej arytmetycznej x= X - X z kreską - takie wyniki określa się mianem odchyleń. Ich średnia równa jest 0, a odchylenie standardowe s. Podzielnie odchylenia od średniej, przez odchylenie standardowe daje nam Z, czyli wyniki standardowe.
Z= X - Xśr / s
Wyniki standardowe maja średnia = 0 i odchylenie standardowe 1 .
5.9 Zalety wariancji i odchylenia standardowego
Wariancja i odchylenie latwiej się poddaja działania matematycznym niż inne miary.
5.10 Momenty średniej.
Średnia i odchylenie standardowe są ściśle powiazane z rodziną statystyk opisowych zwanych MOMENTAMI.
5.11 Miary skośności i kurtozy
Skośność:
g1 = m3 / m2 √m2
Gdy g1=0 - rozkład symetryczny
Gdy g1<0 - rozkład lewoskośny, skośny ujemnie. Przewaga wysokich wyników
Gdy g1>0 - rozkład prawoskośny. Przewaga niskich wyników
Kurtoza:
g2= ( m1 / m2 ²) - 3
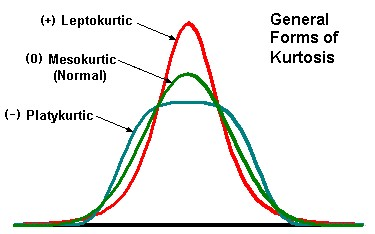
-Gdy g2=0 - rozkład normalny
-Gdy g2<0 - rozkład platykurtyczny (rozpłaszczony)
-Gdy g2>0 - rozkład leptokurtyczny (spiczasty)
RODZDZIAL 6 - PRAWDOPODOBIEŃSTWO I ROZKŁAD DWUMIAROWY.
6.1 Wprowadzenie
6.2 Istota prawdopodobieństwa
Terminu prawdopodobieństwo można używać subiektywnie określając nim pewną postawę lub wątpliwość dotyczaca jakiegos zdarzenia przyszłego.
Druga możliwośc to ujmowanie prawdopodobieństwa wystapienia pewnego zdarzenia w postaci stosunku liczby przypadków pożądanych do całkowitej liczby przypadków mających jednakowa możliwość wystapienia.
Trzecie stanowisko wobec prawdopodobieństwa wiąże się z pojęciem liczebności względnych. Jeśli przeprowadzamy serie prób, powiedzmy N prób , i dane zdarzenie wystepuje w tej serii r razy to r/N jest liczebnościa względną. Te liczebnośc względna można uważać za oszacowanie liczebności p. Prawdopodobieństwo jest parametrem populacji.
6.3 Możliwe wyniki.
6.4 Prawdopodobieństwo łączne i warunkowe.
6.5 Dodawanie i mnożenie prawdopodobieństwa.
6.6 rozkład prawdopodobieństwa.
6.7 Premutacje i kombinacje.
6.8 rozkład dwumianowy
6.9 Właściwości dwumianu
ROZDZIAŁ 7 - KRZYWA NORMALNA
![]()
![]()
![]()
![]()
![]()
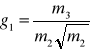
![]()
Wyszukiwarka
Podobne podstrony:
Tkaczyk skrypt, Pomoc Psychologiczna
SKRYPT DO PSYCHOLOGII KLINICZNEJ I PSYCHOPATOLOGII
skrypt+rozwojówka22, Psychologia, Psychologia rozwojowa
skrypt socjologii3, Psychologia, Socjologia
Psychologia uczenia się i pamięci - Skrypt Slajdy, Psychologia uczenia się i pamięci E.Czerniawska
SKRYPT jagodzińska, Psychologia uczenia się i pamięci E.Czerniawska
skrypt filozofia, PSYCHOLOGIA, I ROK, Filozofia, skrypty i podsumowanka
skrypt Miziolek, Psychologia
Skrypt z Kozieleckiego, Psychologia, Semestr I, Wprowadzenie do psychologii
Psychologia przemysłowa - skrypt 2010, Psychologia, Psychologia Przemysłowa
skrypt z politycznej, Psychologia UMCS (2007 - 2012) specjalność społeczna, Psychologia polityczna
Skrypt - pedagogika, psychologia i pedagogika
Tkaczyk skrypt, Pomoc Psychologiczna
Psychologia1, II semestr, Skrypty
więcej podobnych podstron