LABORATORIUM FIZYKI II			Ćwiczenie nr: 1
Wydział: WIP	Grupa: MT-71	Zespół: 8	Data wykonania: 12.01.2004r.
Nazwisko i imię: Łukasz Rzewnicki			Ocena	Przygotowanie:
Sprawozdanie przyjęto:	Data:	Podpis:
									Zaliczenie
Prowadzący: dr Piotr Kurek

Sprawozdanie

Temat: Charakterystyka robocza i czas martwy licznika Geigera-Mullera

Cel ćwiczenia:

Ćwiczenie miało na celu zapoznanie nas z budową i zasadą działania licznika Geigera-Müllera. Ponadto musieliśmy wyznaczyć charakterystykę roboczą licznika Geigera-Müllera, czas martwy licznika oraz poznanie statystycznych praw opisujących rozpad promieniotwórczy.

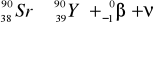
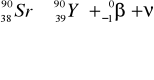
ZASADA DZIAŁANIA LICZNIKA GEIGERA-MULLERA

• Jonizacja gazu znajdującego się w komorze licznika na skutek przejścia przez nią cząstki naładowanej lub kwantu
  

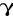
• Wprawienie elektronów i jonów w ruch pod wpływem pola elektrycznego ku anodzie i katodzie,

• Wzbudzanie i jonizowanie dalszych atomów gazu, spowodowane wzrostem energii, do której to elektrony i jony zostały przyspieszone w polu elektrycznym,

• Emisja promieniowania ultrafioletowego

• Proces fotojonizacji rozprzestrzeniania wyładowania elektryczne na całą objętość komory licznika,

• powstaje wyładowanie lawinowe, czyli na obwodzie powstaje impuls napięcia, który jest „sygnałem na wyjściu”, że przez licznik przeszła cząstka jonizująca lub kwant γ;

• następnie licznik zostaje wygaszony by mógł zarejestrować następną cząstkę lub kwant γ;

POMIAR MOCY DAWKI

Pierwszym etapem ćwiczenia był pomiar mocy dawki pochłoniętej za pomocą radiometru. Urządzenie to pozwala na badanie mocy dawki pochłoniętej od dwóch stron: cienkościennej i grubościennej.

Otrzymaliśmy następujące wyniki:

-od strony grubościennej licznik wskazał 2,5 μGy/h

-od strony cienkościennej licznik wskazał 50 μGy/h

Wyniki pomiarów świadczą o tym, że promieniowanie jest bardzo mało przenikliwe. Strona grubościenna detektora powstrzymała niemal całe promieniowanie próbki. Możemy zatem wnioskować, że mamy do czynienia z promieniowaniem β.

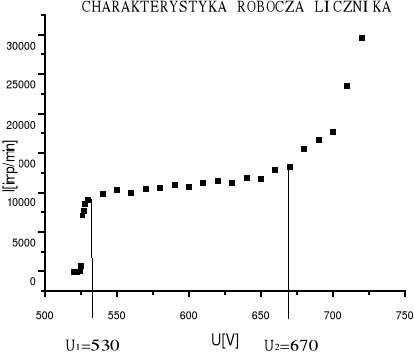
CHARAKTERYSTYKA ROBOCZA LICZNIKA

Celem określenia charakterystyki licznika jest określenie przedziału napięć, w którym licznik będzie rejestrował impulsy.

Pomiary wykonywaliśmy dla stałego czasu

Wyniki pomiarów:

U[V]	520	521	522	524	525	526	527	528	530	540	550	560	570	580	590
N [imp]	1	1	1	8	130	1192	1282	1443	1522	1641	1725	1658	1745	1768	1835
I [imp/min]	6	6	6	48	780	7152	7692	8658	9132	9846	10350	9948	10470	10608	11010
ၳ	0,32	0,32	0,32	0,89	3,61	10,92	11,32	12,01	12,34	12,81	13,13	12,88	13,21	13,30	13,55
U[V]	600	610	620	630	640	650	660	670	680	690	700	710	720
N [imp]	1795	1883	1916	1884	1986	1966	2163	2220	2603	2784	2960	3921	4948
I [imp/min]	10770	11298	11496	11304	11916	11796	12978	13320	15618	16704	17760	23526	29688
ၳ	13,40	13,72	13,84	13,73	14,09	14,02	14,71	14,90	16,13	16,69	17,20	19,80	22,24

Otrzymałem następujący wykres: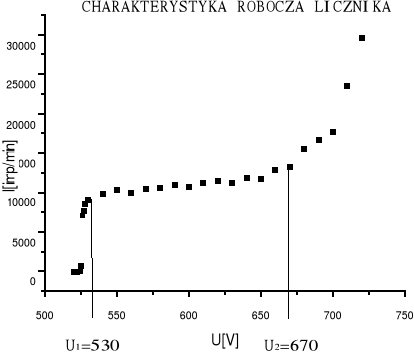

Długość plateau:

CZAS MARTWY LICZNIKA

Nr preparatu	T[min]	N[imp]	I [imp/min]
1	4	43844	10935
1+2	4	94109	23389
2	4	55508	14197

BADANIE STATYSTYCZNEGO CHARAKTERU PRZEMIANY PROMIENIOTWÓRCZEJ

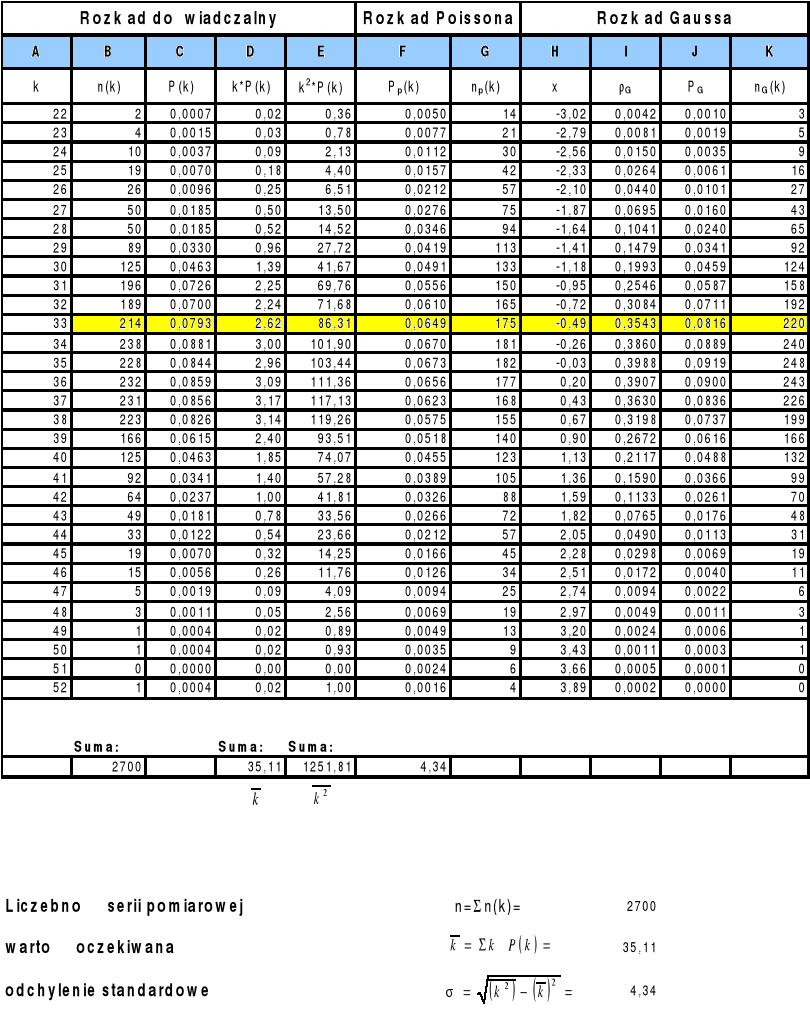
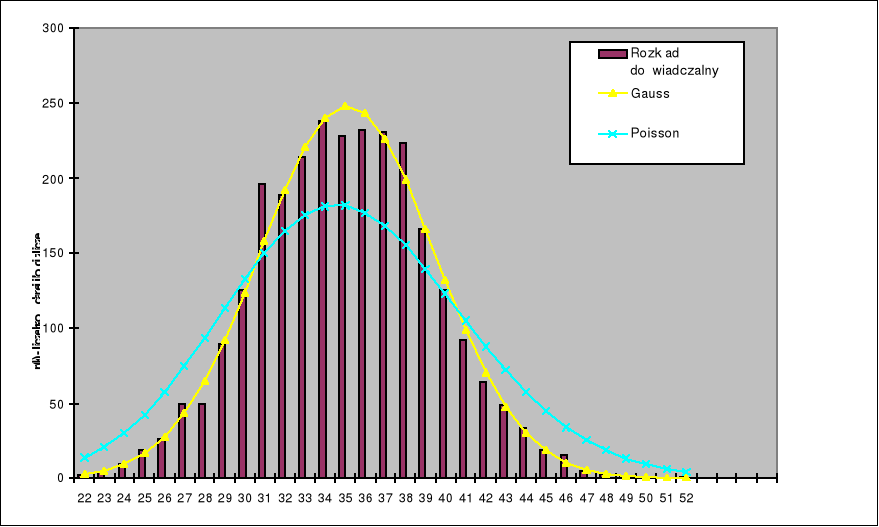
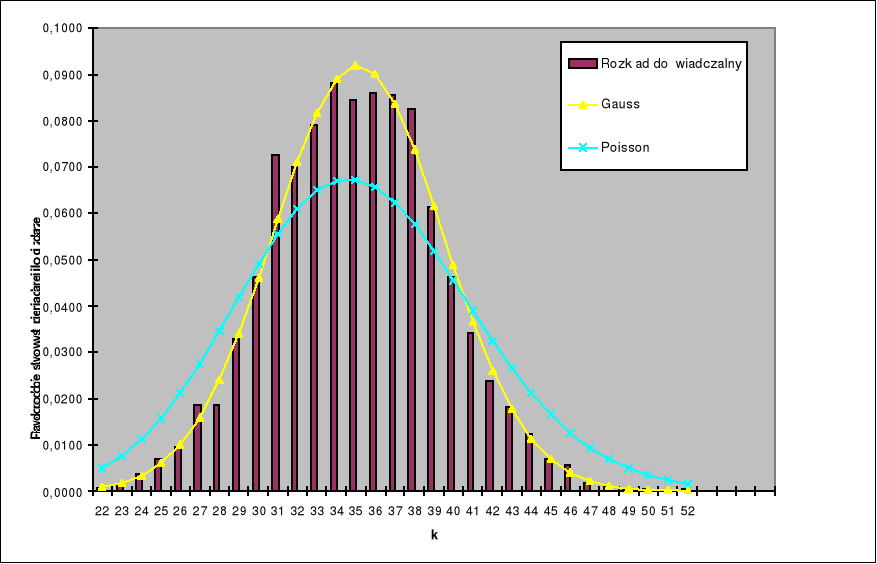
HISTOGRAMY

Przykładowe obliczenia dla zmiennej k= 37

• prawdopodobieństwo doświadczalne

• rozkład Poissona

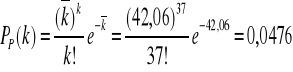
• rozkład Gaussa

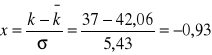
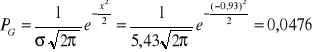
WNIOSKI

Dzięki ćwiczeniu zapoznałem się z procesami przemian promieniotwórczych. Jak widać proces ten jest procesem przypadkowym, który możemy opisać za pomocą funkcji prawdopodobieństwa.

W naszym przypadku wyniki otrzymane w doświadczeniu pokrywają się z rozkładami Gaussa lub Poissona.

---