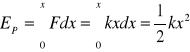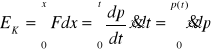Równania Lagrange'a

Równania mechaniczne + elektryczne
formalizm Lagrange'a (równania)

Magazyny energii potencjalnej:

a)	Sprężyna o sztywności k
b)	Sprężyna skrętna o sztywności skrętnej K	m - moment (lub T)
c)	Kondensator o ładunku Q

Magazyny energii kinetycznej:

a)	Poruszająca się masa , ponieważ	- koenergia dla
b)	Masa w ruchu obrotowym (o bezwładności J)
c)	Cewka

Układ cewek: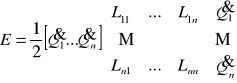

Dla układów fizycznych

Współrzędna uogólniona:

Prędkość uogólniona:

Pęd uogólniony
(kręt)
(strumień sprzężony)

Ogólna funkcja Lagrange'a

Równanie Lagrange'a:
dla każdej współrzędnej uogólnionej, gdzie:
- siła uogólniona,
- siła dyssypacji działająca wzdłuż i-tej współrzędnej.

		Cewki 1,2 są takie same 4 bramy energetyczne: 3 cewki + wał
	cewka 3 + żłobki
	cewka 1 & 2 + rzut izometryczny

Zakładamy model monoharmoniczny (sinusoidalny przebieg indukcyjności) i dlatego przybliżamy model sinusem.

Równania Lagrange'a (tyle ile bram)

1. równanie mechaniczne:

/
/

[
moment elektromagnetyczny]

2. równanie elektryczne dla uzwojenia 1:

/
/

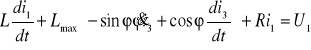
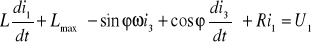
Stan ustalony maszyny synchronicznej 2-fazowej:

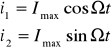
prąd 2-fazowy symetryczny (przesunięcie
)

(prąd wzbudzenia) (3 - uzwojenie wzbudzenia)

(bo
)

- nie

zależy od czasu

Stojan wytwarza pole magnetyczne wirowe kołowe, ze względu na postać
i
.

wykres fazorowy (wskazowy)

WYKRESY skrypt Jan Rusek „Elektrotechnika z elementami napędów” str. 108

Dążymy do
aby minimalizować straty energii na ciepło.

Generator - turbina napędza nasz silnik

Motor - maszyna robocza obciąża nasz silnik

[
oznaczenie wartości skutecznych]

zał: 1) zasilanie z sieci sztywnej (o stałym napięciu)

2)

WYKRESY skrypt Jan Rusek „Elektrotechnika z elementami napędów” str. 109

- prąd wzbudzenia idealnego biegu jałowego.

Sytuację normalnej pracy przedstawia wykres „c” - maszyna przewzbudzona (zachowuje się jak kondensator)

4

Luke ELEKTROTECHNIKA-wykład 19.2.2k+2

#

---