Wyznaczanie masowego współczynnika pochłaniania pro­mieniowania gamma dla różnych ciał

Wstęp:

Jądra poszczególnych pierwiastków składają się z protonów i neutronów, czyli nukleonów. Protony są cząstkami elementarnymi o ładunku dodatnim, rów­nym co do bezwzględnej wartości ładunkowi elektronu, tj. e=1.602110^-19C. Masa spoczynkowa protonu wynosi m_p= 1.6725 10^-27 kg. Neutrony są cząst­kami elementarnymi elektrycznie obojętnymi o masie spoczynkowej równej m„= 1.674810^-27 kg. Nukleony są cząstkami cięższymi od elektronów o ok. 1836 razy. Jądro atomu o ładunku Ze i liczbie masowej A zawiera Z protonów i N=(A-Z) neutronów.

Siły kulombowskiego oddziaływania między protonami w jądrze są elementem destrukcyjnym, szczególnie dla jąder ciężkich. W związku z tym pierwiastki o liczbie atomowej powyżej 82 są zaliczane do pierwiastków nietrwałych i mogą ulegać naturalnemu rozpadowi. Wszystkie przemiany jądrowe, za­równo wysokoenergetyczne jak i niskoenergetyczne, podlegają następującym zasadom:

- zachowania ładunku elektrycznego;

- zachowania całkowitej liczby nukleonów (suma liczb masowych przed reakcją i po reakcji musi być taka sama);

- zachowania masy - energii (dla układu izolowanego całkowita ener­gia układu pozostaje stała);

- zachowanie pędu i momentu pędu.

Przemiany jądrowe, w wyniku których są emitowane cząstki ၡ, ၢ lub towarzyszące im promieniowanie ၧ, podlegają statystycznemu prawu, zwanemu prawem rozpadu, które ma postać:

N = N₀exp(-ၬt)

gdzie:

N₀ −liczba jąder w chwili t = 0

N −liczba jąder, które po czasie t nie uległy jeszcze rozpadowi,

ၬ − stała rozpadu,

t −czas.

Stałą rozpadu definiuje się jako prawdopodobieństwo zaistnienia rozpadu jądra danego pierwiastka w jednostce czasu. Czas jaki upłynie od chwili roz­padu jądra do rozpadu następnego jądra danego pierwiastka, nazywa się cza­sem życia τ. Zależność zachodząca między czasem życia a stalą rozpadu jest następująca:

Czasy życia większości pierwiastków promieniotwórczych są bardzo długie, wprowadzono więc czas połowicznego rozpadu T. Czas połowicznego rozpadu jest to czas, po którego upływie początkowa liczba N₀ jąder w wyniku rozpadu zmaleje do połowy, tzn. N=1/2N₀. Zależność zachodząca pomiędzy czasem połowicznego rozpadu a czasem życia jest następująca:

T = τ In 2=0.693 τ

Promieniowanie y jest promieniowaniem elektromagnetycznym o takim zakresie długości fali jak promieniowanie rentgenowskie, tj. od l • 10^-10 m do 2 • 10^-8 m. Nie powoduje ono zatem ani zmiany ładunku, ani zmiany masy atomowej pierwiastka, który jest jego źródłem. Promieniowanie ၧ nie stanowi niezależnego zjawiska promieniotwórczości naturalnej, a jedynie towarzyszy rozpadom ၡ, lub ၢ. Emisja promieniowania ၧ towarzyszy rozpadowi ၡ lub ၢ tylko wtedy, gdy jądro nowo powstającego pierwiastka znajduje się w stanie energetycznie wyższym niż jego stan podstawowy. Atom, którego jądro wysyła kwanty y, powinien w rezultacie konwersji wewnętrznej wysyłać jednocześnie charakterystyczne promieniowanie rentgenowskie.

Podczas przechodzenia przez materię równoległej wiązki promieniowania γ następuje jej pochłanianie i rozpraszanie. Natężenie wiązki promieniowania po przejściu przez materię o grubości x opisuje prawo Lamberta-Bougera

I = I₀exp(-μd)

gdzie:

I₀ - natężenie wiązki padającej,

μ - liniowy współczynnik osłabienia [cm^-1].

Liniowy współczynnik μ równa się względnemu zmniejszeniu natężenia wiązki promieniowania γ na drodze o jednostkowej długości:

Liniowy współczynnik osłabienia jest równy sumie liniowych współczyn­ników pochłaniania rzeczywistego τ i rozpraszania σ.

μ = τ + σ

Ponieważ współczynniki τ i σ są proporcjonalne do masy ciała pochłania­jącego , w praktyce jest stosowany masowy współczynnik osłabienia:

μ_m = μ/ρ = τ_m + σ_m.

Masowy współczynnik pochłanianiaτ_m jest zależny od liczby atomowej absorbenta, jego masy atomowej oraz długości fali padającego promieniowania w następujący sposób:

gdzie:

c − stała,

N_o − liczba Avocado

A − masa atomowa pierwiastka pochłaniającego.

Wyniki:

POMIAR TŁA It
1		98
2		116
3		135
4		123
5		141
6		156
7		151
8		141
9		104
10		139
średnie		130,4
błąd śred.		18,4
I0
1		3682
2		3691
3		3672
4		3618
5		3689
srednia		3670,4
błąd śred.		19,1

MOSIĄDZ
NR	GR [m]	I1	I2	I4	I5	I średnie	Δ I śred.	ln(Io/I)	Δ ln(io/I)
1	0,00238	3364	3356	3329	3353	3350,5	8,3	0,09119	0,0077
2	0,00477	3096	3122	3060	3085	3090,75	14,1	0,1718	0,0098
3	0,00741	2777	2830	2839	2826	2818	15,3	0,2642	0,0106
4	0,01	2646	2568	2570	2561	2586,25	21,9	0,35	0,0137
5	0,01241	2349	2313	2315	2360	2334,25	13,0	0,4526	0,0108
6	0,015	2130	2144	2108	2074	2114	16,7	0,5517	0,0131
7	0,018	1974	1895	1903	1949	1930,25	20,6	0,6426	0,0159
8	0,02	1614	1703	1708	1753	1694,5	31,9	0,7729	0,024
9	0,02344	1484	1562	1549	1571	1541,5	21,6	0,8675	0,019
10	0,02645	1356	1330	1294	1378	1339,5	19,8	1,008	0,02
11	0,02914	1282	1197	1225	1198	1225,5	21,8	1,0969	0,023
12	0,03216	1145	1087	1105	1125	1115,5	13,7	1,19	0,0175
13	0,03517	996	935	972	1028	982,75	21,5	1,3177	0,027
					średnie	2009,48	18,47

OŁÓW
NR	GR [m]	I1	I2	I4	I5	I średnie	Δ I śred.	ln(Io/I)	Δ ln(io/I)
1	0,00408	2579	2614	2568	2581	2585,5	10,9	0,3503	0,0094
2	0,00855	1760	1741	1764	1799	1766	13,2	0,7315	0,0127
3	0,01265	1213	1199	1286	1208	1226,5	22	1,0961	0,0231
4	0,01672	868	801	827	888	846	21,5	1,4675	0,03
5	0,0199	621	635	595	638	622,25	10,7	1,7747	0,0224
6	0,02307	518	527	500	487	508	9,8	1,9775	0,0245
7	0,0258	411	379	396	390	394	7,3	2,2317	0,0237
8	0,02885	302	290	300	339	307,75	11,8	2,4787	0,0434
9	0,03187	285	282	243	254	266	11,4	2,6245	0,0479
					średnie	946,8889	13,178

STAL
NR	GR [m]	I1	I2	I4	I5	I średnie	၄ I śred.	ln(Io/I)	၄ ln(io/I)
1	0,00443	3277	3141	3191	3247	3214	33	0,1327	0,0154
2	0,00884	2676	2795	2858	2759	2772	41,6	0,2807	0,02
3	0,01324	2416	2404	2366	2419	2401,25	13,4	0,4243	0,01
4	0,01764	2024	2070	2009	2020	2030,75	14,7	0,5918	0,0124
5	0,02219	1691	1715	1753	1718	1719,25	14	0,7584	0,0133
6	0,0268	1475	1416	1458	1437	1446,5	14	0,9311	0,0148
7	0,03121	1240	1222	1252	1259	1243,25	8,9	1,0825	0,0123
8	0,03561	1085	1072	1094	1094	1086,25	5,7	1,2175	0,0104
9	0,04002	944	878	876	936	908,5	20	1,3962	0,0272
10	0,04444	803	818	745	780	786,5	17,4	1,54	0,0273
11	0,04887	637	685	686	664	668	12,6	1,7037	0,024
12	0,0533	579	611	566	603	589,75	11,4	1,8283	0,0245
					średnie	1572,167	17,23

Wartości, które zostały odczytane z wykresu;

	stal [m]	ołów [m]	mosiądz [m]
I=f(d)	0,024	0,015	0,023
lnI0/I=f(d)	0,029	0,012	0,027
średnie	0,0265	0,0135	0,025

Obliczenie współczynnika pochłaniania ze wzoru:

I = I₀exp(-μd)

gdzie:

I − są to średnie wartości dla każdego każdego materiału podane w tabelach

I₀= 3670,4 − jest wartością średnią natężenia wiązki padającej

d − średnica odczytywana z wykresów

μ_{m −} wyznaczaliśmy ze wzoru:

gdzie:

- obliczony współczynnik

- gęstość bezwzględna [kg/m³]

	ρ [kg/m^3]	μ [m^-1]	Δμ	μm
stal	7800	31,99418	0,4894	0,0041
ołów	11300	100,361	0,6732	0,00888
mosiądz	8400	24,09697	1,3209	0,00287

Rachunek błędu:

Wzór na błąd średniej

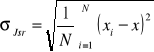
Wzór na obliczenie błędu ΔlnI/I₀

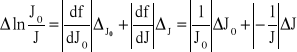
Wzór na obliczenie współczynnika μ

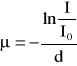
Wzór na błąd obliczenia μ

=

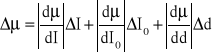
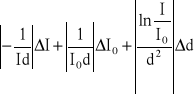
Wyniki obliczeń są zestawione w tabelach powyżej.

5

---